高速旋转飞行弹丸外弹道表面温度场研究
张俊,刘荣忠,郭锐,邱荷,刘萌萌
(南京理工大学 机械工程学院,江苏 南京210094)
0 引言
红外跟踪捕获飞行目标的前提是掌握其表面的温度特征,科研人员针对飞行目标的温度场或红外辐射特性进行了大量研究,主要包括卫星、飞机、导弹、超声速或高超声速飞行器等[1-4]。然而,对于低马赫数飞行弹丸的相关研究较少,并且在计算气动加热时,很少考虑弹丸高速旋转产生的影响。文献[5]应用热网络法建立了弹丸表面温度场的理论计算模型,但是,在求解时没有明确指出弹道模型与表面温度场的耦合求解方法。文献[6]以此为切入点,在质点弹道模型的基础上,研究弹丸的表面温度场和红外辐射特性,将运动状态和表面温度场联系起来,但没有得出不同部位的温度差异。
空中目标高速旋转飞行产生的气动热是其表面的主要红外辐射源,另外,气动热也是高速飞行目标设计初期必须要考虑的热防护因素,属于一种复杂的有旋流动对流换热,应用CFD 软件通过使用旋转坐标系并设置流场边界条件可以得到其瞬态解[7],但是,整个飞行过程是一个受弹道诸元和气流物性不断变化而控制的相互影响、不可分割的整体,仅计算有限飞行时刻点下的稳态值,难以满足红外跟踪探测的需要。
本文速度和角速度产生的气动热分别按照高速气流纵掠和绕流对流换热理论计算,通过耦合求解弹道模型和热流平衡方程组,得到了弹道诸元和表面温度场的变化规律,最后分析了不同发射条件和气流温度对其平均温度场的影响规律。
1 旋转飞行弹丸的六自由度弹道模型
以某155 mm 口径炮射末敏母弹为例[8],建立弹道模型,首先,基于牛顿第二定律建立弹道坐标系下的质心运动方程组,得到质心运动方程的标量形式和质心的位置变化方程组:
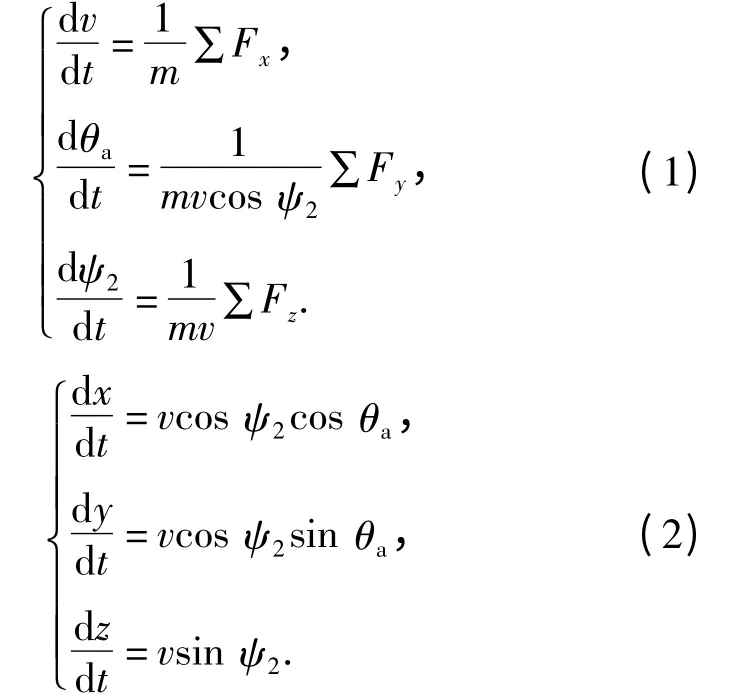
式中:m、v 分别为弹丸的质量和速度;θa为速度高低角;ψ2为速度方位角;Fx、Fy和Fz分别为作用在弹丸上的力在弹道坐标系上的分量;x、y 和z 为弹丸的质心坐标。
其次,基于动量矩定理建立弹轴坐标系下的绕心运动方程组,得到弹丸绕心转动的运动学方程组与动力学方程组:
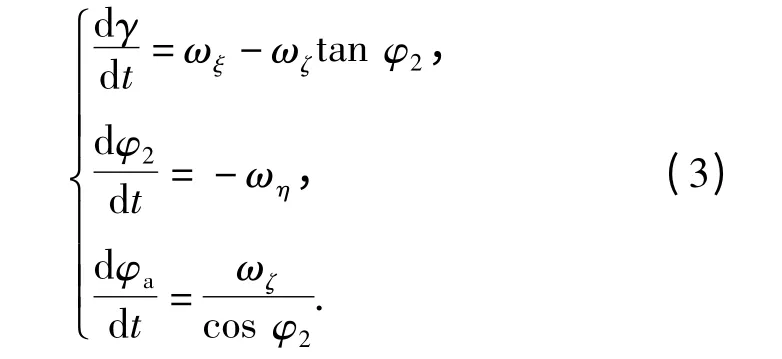
式中:γ 为弹体坐标系相对于弹轴坐标系的转角;φ2为弹轴方位角;φa为弹轴高低角;ωξ、ωη和ωζ分别为弹丸的角速度在弹轴坐标系上的分量。

式中:Mξ、Mη和Mζ分别为作用在弹丸上的力矩在弹轴坐标系上的分量;A 为赤道转动惯量;C 为极转动惯量;β1、β2分别为弹丸的惯性主轴在弹体坐标系上的投影与其坐标轴的夹角。
最后,加上描述坐标系角度的约束方程,组成旋转飞行弹丸的六自由度(6-DOF)弹道模型,当给定初始条件和相关气动参数后,即可求出弹道诸元随飞行时间的变化规律。
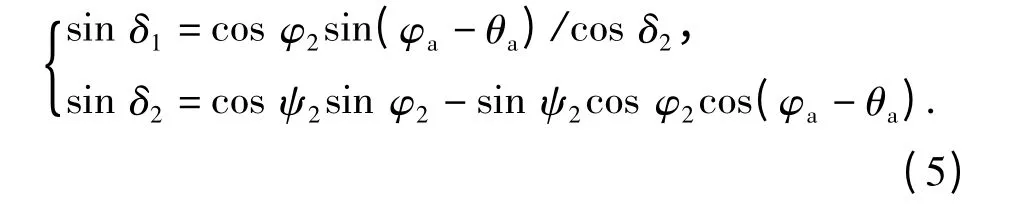
式中:δ1为高低攻角,δ2为方向攻角,用于确定弹轴相对于速度的方位和计算空气动力。
2 旋转飞行弹丸的表面温度场模型
2.1 节点热流平衡方程
由于弹丸的飞行时间短,壁厚薄,忽略其在厚度方向上的热量传递,实际上,厚度方向应按照集总参数法考虑,因此计算出来的温度低于实际温度,壁厚越大误差越明显。将弹头部近似看作圆锥体,将其表面按照面元面积相等的规则进行划分,以每个单元的中心作为计算节点,对各节点所在的热传递网络建立热流平衡方程
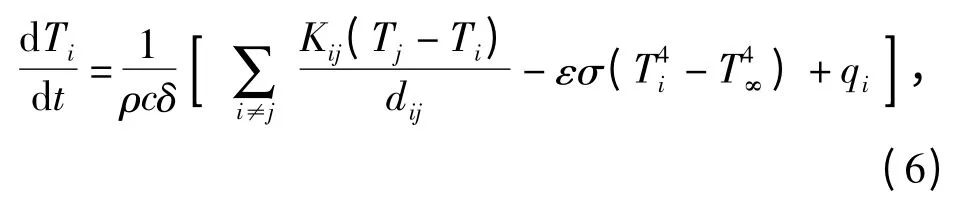
式中:ε 为弹丸表面的半球总发射率,指所有方向和所有波长下的平均值,与表面温度、粗糙度以及涂层的存在有关,设弹丸表面满足灰体漫射性质,则发射率一定;ρ、c 分别为表面材料的密度和比热容;δ 为壁厚;dij、Kij为相邻节点间的距离和热传导因子;T∞为来流气温;Ti为节点i 的温度;Tj为与节点i 相邻节点的温度;qi为该面元吸收的外热流,包括:气动加热、弹丸腔内电子器件发热、太阳直接辐射、地球反射的太阳辐射以及地球热辐射等。相比气动热,环境热辐射和内热源的影响较小,可忽略不计。
2.2 高速旋转飞行弹丸气动对流换热
弹丸圆柱部表面由于速度产生的气动加热按照高速气流纵掠平壁换热理论计算,角速度产生的气动加热按照高速气流绕流圆柱换热理论计算,弹头部表面的气动加热根据绕流锥体与绕流柱体之间的换热关系计算。
气流在绝热条件下相对于弹丸被滞止的温度称为绝热壁温或驻点温度
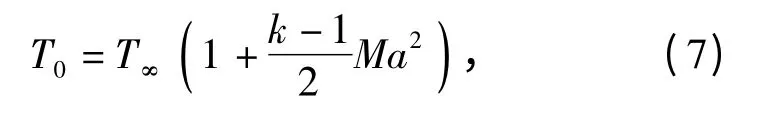
式中:k 为空气绝热指数;Ma 为马赫数,Ma = v/a,v 为弹丸的飞行速度,a 为声速。
若弹丸发射点取标准海平面大气参数,则来流气温与压强随飞行高度的变化关系为
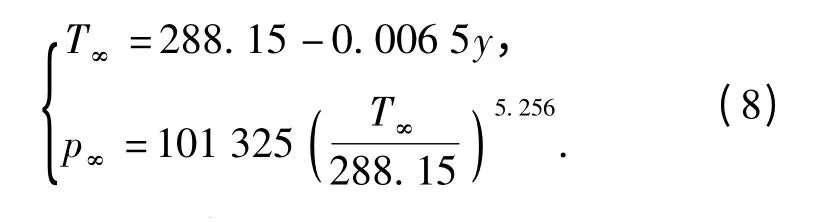
由于气流相邻各层间伴随着热与功的相互转换,使得恢复温度Tr小于绝热壁温,因此,引入温度恢复系数r,表征受阻气体的实际动力温升,层流时r=0.84,湍流时r=0.89.

局部气动对流换热系数
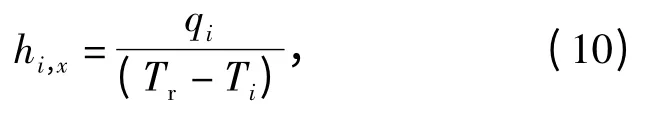
式中:qi为局部气动热流密度,包括由速度产生的qi1和由角速度产生的qi2.
弹丸圆柱部表面由于速度产生的气动加热按照高速气流纵掠平壁的实验关联式计算[9]
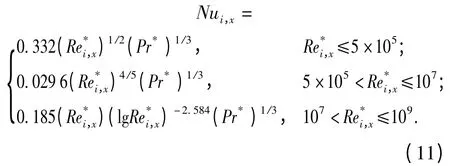
式中:Nui,x为局部努赛尔数,Nui,x=xhi,x/λ*,x 为计算节点到弹头的距离,λ*为空气导热系数为局部雷诺数;Pr*为普朗特数;参考温度和气流导热系数
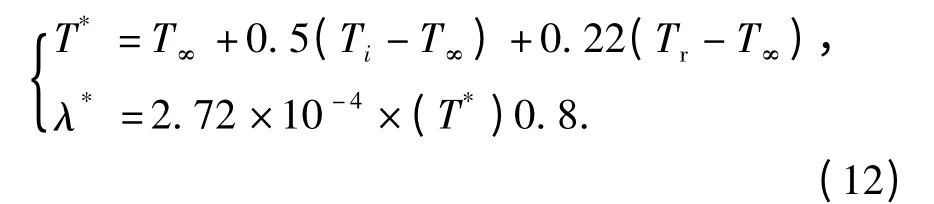
参考温度下的局部雷诺数与普朗特数[10]
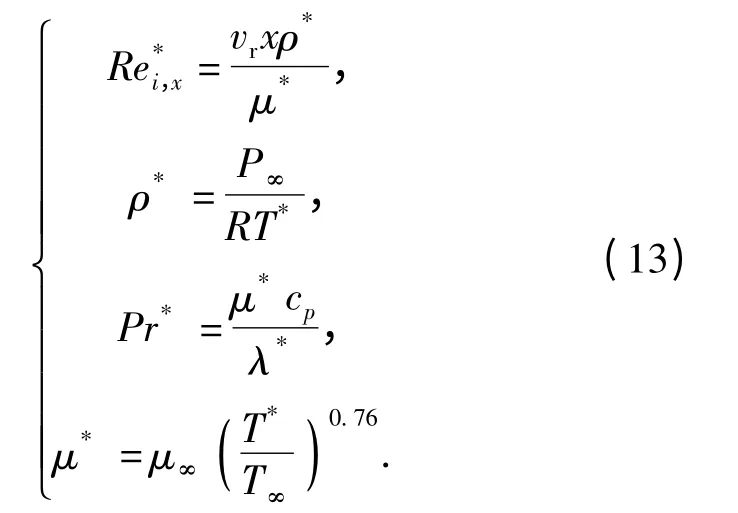
式中:μ*与ρ*分别为空气动力黏度和密度;cp为定压比热;* 号表示在参考温度下的量。
将(9)式、(11)式代入(10)式,得到弹丸圆柱部表面由于速度引起的局部气动热流密度

弹丸表面由于高速旋转产生的气动加热根据Hilpert 绕流圆柱对流换热的实验关联式计算
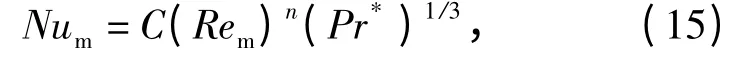
式中:Rem为平均雷诺数,Rem=ωρ*d2/2μ*,ω 为弹丸的旋转角速度,d 为弹丸外径;C、n 由此雷诺数确定[9];此处近似认为局部雷诺数等于平均雷诺数。
将(9)式、(15)式代入(10)式,得到弹丸圆柱部表面由于旋转产生的局部气动热流密度

联立(14)式、(16)式得出弹丸圆柱部表面的局部气动热流密度为

弹头部表面的局部气动热流密度按照绕流锥体与绕流柱体间的换热关系得出[11],热流密度在层流时为(17)式的1.732 倍,湍流时为1.176 倍。
3 数值计算与结果分析
将(6)式各节点的温度表示为时间的微分式,则(1)式~(6)式中的各弹道诸元和节点温度都是关于时间的微分方程,应用四阶Runge-Kutta 法同步求解,即可同时求出弹道诸元和弹丸表面各节点的温度随飞行时间的变化。
3.1 弹丸外弹道表面温度场分布
已知:弹丸外径155 mm;弹头部长400 mm;圆柱部长500 mm;弹丸质量45 kg;壁厚4 mm;表面材料热导率22.6 W/(m·K);发射角45°;发射速度650 m/s;初始转速200 r/s;发射点取标准海平面大气参数;弹丸表面初始温度300 K;发射率0.8;计算时间50 s.
图1 为弹丸速度随飞行时间的变化曲线,图2为弹丸自转角速度随飞行时间的变化曲线,图3 为绝热壁温、恢复温度、气流温度以及两个节点的定性温度随飞行时间的变化曲线。
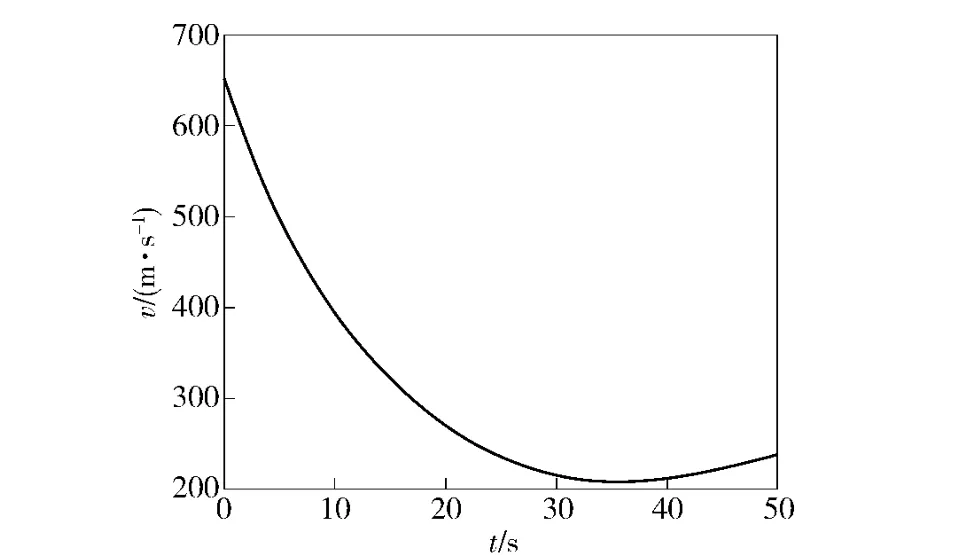
图1 弹丸的速度曲线Fig.1 Velocity curve of projectile
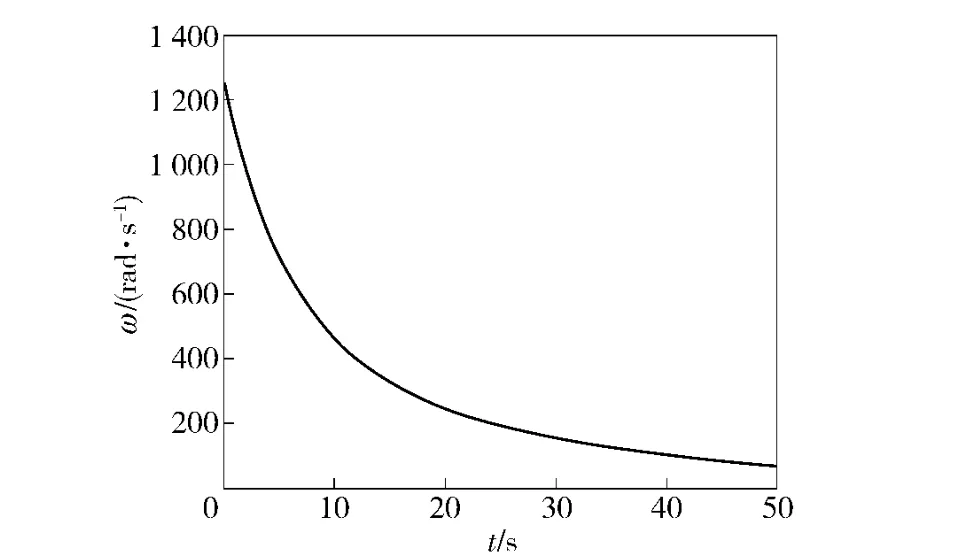
图2 弹丸的自转角速度曲线Fig.2 Angular velocity of rotation curve of projectile
图1得出:弹丸出炮口后在重力和空气阻力的作用下,速度迅速降低,上升至弹道最高点后,在重力作用下,速度反向增加。图2 得出:弹丸的自转角速度在极阻尼力矩作用下呈指数衰减,在弹道末段下降幅度逐渐变缓,符合外弹道学弹丸自转角速度衰减理论。图3 得出:绝热壁温以及恢复温度的变化规律都与速度的变化规律基本一致;气流温度先随飞行高度增加而减小,后随飞行高度下降而逐渐增加;弹丸在飞行过程中的绕流物性参数由定性温度确定,定性温度由来流气温,各节点的温度以及恢复温度共同决定,由于各节点的温度随飞行时间不断变化,所以每个节点对应一个定性温度。

图3 绝热壁温、恢复温度、气流温度和定性温度的变化Fig.3 Variations of adiabatic wall,recovery,airflow and qualitative temperatures
图4为弹丸表面的温度场分布。结果表明:弹丸出炮口后,表面各部位的温度迅速升高,越靠近弹头部,温度升高速率越快,峰值温度越高,这是由于越靠近弹头部,气动对流换热系数越大;随着速度逐渐减小,气动加热逐渐减弱,甚至有可能转变为气动降温,并且辐射散热量与其温度的四次方成正比,热量散失较快,所以弹丸表面温度迅速下降;靠近弹头处的节点温度和弹丸的速度表现出了很强的跟随性,在弹道末段上,温度变化率较大,这是由于靠近弹头位置上的温度较高,弹丸的速度降低后,气动降温显著,当弹丸速度反向增加后,温度也随之增加。对比图3、图4 得出:节点的定性温度与其温度场的变化基本相近。

图4 弹丸表面的温度场分布Fig.4 Temperature field distribution on the surface of projectile
3.2 不同发射条件和气流温度下的平均温度场
计算不同发射条件和气流温度下的平均值,总结各因素对其平均温度场的影响规律,除对应的影响因素外,其余已知条件同3.1 节。

图5 不同初速下弹丸表面的平均温度场Fig.5 Average temperature fields at different initial velocities
图5为不同初始速度下弹丸表面平均温度的变化规律,图6 为不同初始转速下弹丸表面平均温度的变化规律。图5 表明:弹丸表面平均温度的变化率随初始速度增加而非线性增加,初始速度越高,温度升高速率越快,峰值温度越高,同时温度下降速率也越快,这是由于速度越高,局部换热系数越大,气动对流换热越强烈,并且随着初速增加,局部换热系数呈非线性增加趋势;弹丸的初速越高,达到热平衡所需要的时间越长,初速550 m/s 时,约30 s 后稳定在320 K 左右,初速650 m/s 时,约40 s 后才稳定到320 K,此后与环境温度相差40 ~50 K.图6 表明:弹丸的高速旋转角速度对其表面温度场的影响较小,初始转速较低时,其影响可忽略不计,随着初始转速增加,表面温度的峰值温度和温度变化率增加。这里需要指出:实际上弹体表面的气动加热属于一种复杂的有旋流动对流换热,受弹丸的速度、转速、气流物性参数共同控制,分别讨论只能作为一种近似的考虑方法。
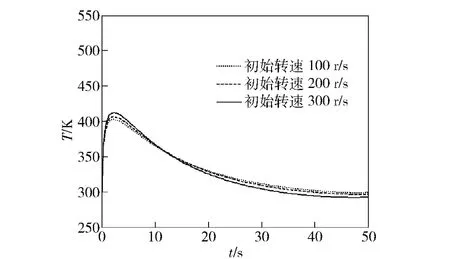
图6 不同初始转速下弹丸表面的平均温度场Fig.6 Average temperature fields at different initial rotational speeds
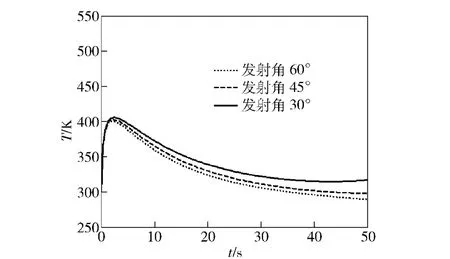
图7 不同发射角下弹丸表面的平均温度场Fig.7 Average temperature fields at different launching angles
图7为不同发射角下弹丸表面平均温度的变化规律,图8 为不同气流温度下弹丸表面平均温度的变化规律。图7 表明:发射角越小,表面温度越高,但这种规律是在弹丸发射一定时间后,才逐渐显现出来,在出炮口较短时间内,发射角和表面温度的关系不大,在弹道末段上,这种规律最明显。这是由于发射角和速度存在必然联系,发射角越小,在弹道末段上,弹丸在重力作用下的速度越高,气动加热显著。图8 给出了气流温度随飞行高度变化和气流温度不变时的平均温度场,可以看出这两种情况下的差别较大,为了更直观的比较高温和低温发射的差别,在气流温度不随飞行高度变化的情况下,根据弹丸工作规定的气温范围(-40 ℃~+50 ℃),给出了气流温度取最高和最低时的计算结果。结果表明:气流温度对弹丸表面温度场的影响较大,气流温度越高,表面温度上升速率越快,峰值温度越高,达到热平衡时的温度也越高,这是由于气流温度直接影响弹丸表面的恢复温度和定性温度,而恢复温度和定性温度是决定气动对流换热的关键因素。

图8 不同气流温度下弹丸表面的平均温度场Fig.8 Average temperature fields with different airflow temperatures
4 结论
1)气动加热是影响弹丸表面温度场的主要因素,而弹丸的速度、转速、发射角、气流温度以及定性温度都是影响气动加热的关键因素。
2)弹丸表面的温度梯度与距弹头的距离呈反比;表面温度随发射速度增加而非线性增加;初始转速越高,峰值温度和温度变化率越大;发射角越小,表面平均温度越高,在弹道末段上,这种规律最明显;气流温度越高,表面温度上升速率越快,峰值温度越高,达到热平衡时的温度越高。
3)在飞行目标表面温度场或红外辐射特性的相关研究中,可根据目标的结构特征,利用应用广泛且精度较高的经验公式计算其外热流,利用热传导理论建立能量守恒方程,通过耦合求解运动模型与热流平衡方程组,即可得到受运动参数和气流物性所控制的动态温度场分布。高速旋转飞行弹丸的气动加热一定与其角速度密切相关,这一问题的工程计算有待于进一步深入研究。
References)
[1]Zhang J,Wang Y C,Lv X Y,et al.Numerical analysis of infrared characteristics of exoatmospheric ballistic target[J].Infrared and Laser Engineering,2008,37(5):765 -769.
[2]夏新林,艾青,任德鹏,等.飞机整体瞬态热状况的数值仿真研究[J].航空学报,2007,28(3):513 -518.XIA Xin-lin,AI Qing,REN De-peng,et al.Numerical analysis on the transient thermal status of aircraft[J].Acta Aeronautica Et Astronautica Sinica,2007,28(3):513 -518.(in Chinese)
[3]娄文忠,齐斌.火箭弹弹头引信空气附面层热特性数值仿真研究[J].兵工学报,2007,28(4):406 -410.LOU Wen-zhong,QI Bin.Numerical simulation method for thermal characteristic of air boundary layer of rocket fuze[J].Acta Amamentarii,2007,28(4):406 -410.(in Chinese)
[4]侯玉柱,郑京良,董威.高超声速飞行器瞬态热试验[J].航空动力学报,2010,25(2):343 -347.HOU Yu-zhu,ZHENG Jing-liang,DONG Wei.Transient test of aerodynamic heating for hypersonic vehicle[J].Journal of Aerospace Power,2010,25(2):343 -347.(in Chinese)
[5]杨威,张建奇,刘劲松.飞行弹丸红外辐射特性的理论计算[J].红外与激光工程,2005,34(1):42 -45.YANG Wei,ZHANG Jian-qi,LIU Jin-song.Theoretical calculations of infrared radiation of the projectile in flight[J].Infrared and Laser Engineering,2005,34(1):42 -45.(in Chinese)
[6]袁轶慧,张俊举,陈佐龙,等.飞行弹丸表面温度分布与红外辐射特性的仿真研究[J].兵工学报,2010,31(8):1090 -1094.YUAN Yi-hui,ZHANG Jun-ju,CHEN Zuo-long,et al.Simulation study on temperature and infrared radiation characteristics of flying projectile[J].Acta Amamentarii,2010,31(8):1090 -1094.(in Chinese)
[7]王智杰,陈伟芳,李洁.旋转弹丸空气动力特性数值解法[J].国防科技大学学报,2003,25(4):15 -19.WANG Zhi-jie,CHEN Wei-fang,LI Jie.Numerical solution of the aerodynamic properties of the rotating projectiles[J].Journal of National University of Defense Technology,2003,25(4):15 -19.(in Chinese)
[8]杨绍卿,灵巧弹药工程[M].北京:国防工业出版社,2010:106-117.YANG Shao-qing.Smart ammunition engineering[M].Beijing:National Defense Industry Press,2010:106 -117.(in Chinese)
[9]姚仲鹏,王瑞君.传热学[M].北京:北京理工大学出版社,2003:146 -170.YAO Zhong-peng,WANG Rui-jun.Heat transferr[M].Beijing:Beijing Institute of Technology Press,2003:146 -170.(in Chinese)
[10]钱翼稷.空气动力学[M].北京:北京航天航空大学出版社,2004:230 -264.QIAN Yi-ji.Aerodynamic[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2004:230 -264.(in Chinese)
[11]范绪箕.气动加热与热防护系统[M].北京:科学出版社,2003:51 -59.FAN Xu-ji.Aerodynamic heating and thermal protection[M].Beijing:Science Press,2003:51 -59.(in Chinese)

