脉动力作用下充液直管动态特性分析

王孚懋，许宗岭，吴文兵，刘士杰（山东科技大学机械电子工程学院，山东青岛 266590）

管道作为输送流体的绝佳设备，在石油化工、能源动力、市政工程等领域得到广泛的应用。当今工业的快速发展，管道的振动问题越来越引起人们的重视。强烈的管道振动会影响管路的安全，造成管道链接部位出现松动或破裂，轻则造成液体泄漏，重则因管道破裂引起爆炸，导致严重的生产事故[1]。管道振动原因很多，主要涉及两个方面：一是由于动力机械运动机构的动力平衡性差或者基础安装不当而引起管道振动，二是由于输送流体脉动引起管道振动[2]。工程实践表明，在管路中安装柔性连接管或采取减振措施后，管道振动主要由流体脉动产生[3]。由于动力机械如空压机、水泵和液压泵等始端设备做周期性间歇运动，使得管道内流体压力、速度、密度和流量等参数随着时间和位置而变化，形成流体脉动[4]。本文运用Fluent软件分析直管在脉动力影响下直管压力分布，分析脉动压力的特性，采用ANSYSWorkbench软件单向流固耦合模块分析了充液直管的流固耦合振动模态。

1 充液直管内流场基本方程

管道中流体的流动要受物理守恒定律支配，研究流动的基本守恒定律有：质量守恒定律、能量守恒定律、动量守恒定律[5]。对于流动体，如果其中含有不同成分的混合或者各成分之间有相互作用，这样的系统要遵循组分守恒定律。如果所研究的流动处在湍流状态，系统还应该遵循附加的湍流输运方程[6]。

1.1 质量守恒方程

在任何的流动问题中都必须满足质量守恒定律。质量守恒定律可以表述为：单位时间内流体微元体重质量的增加，等于同一时间间隔内流入该微元体的净质量。根据这个定律所述，可以推到出质量守恒方程。

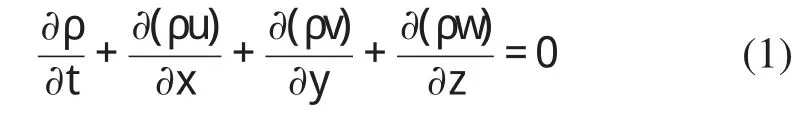
1.2 动量守恒方程

任何的流动都必须满足动量守恒方程，动量守恒方程是流体系统的基本定律。动量守恒定律可以表述为：所选的微元中流体动量对时间的变化率等于所有作用在微元上外界力的合力。动量守恒定律实际上就是牛顿第二定律，按照动量守恒这一定律可以推导出在x、y、z三个方向上的动量守恒方程。

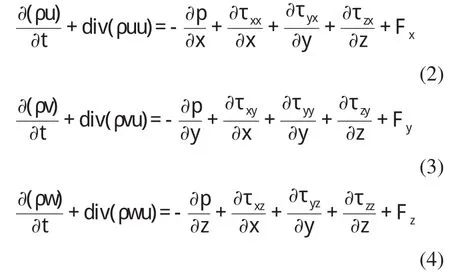
式中ρ为微元流体压力；τxx、τxy、τxz是由于分子具有粘性而作用在微元体表面上粘性应力τ的各个分量；Fx、Fy、Fz是作用在微元体上的体积力，如果体积力只有重力，并且z轴是竖直向上的，则有

Fx=0、Fy=0、Fz=-ρg。

1.3 能量守恒方程

能量守恒方程是含有热交换流动的系统都必须满足的基本方程。这个方程可以描述为：微元体增加的能量是进入微元体的净热流量加上外力对微元体所做的功。可有下表达式来描述能量守恒方程

式中

cp——比热容，

T——温度，

k——流体的传热系数

ST——流体内热源以及由于流体的粘性作用流体机械能转换成热能的部分

1.4 湍流模型

标准k-ε湍流模型在对有强流线弯曲、漩涡和旋转分析时会有很大仿真失真，为此必须对标准k-ε湍流模型进行修正，即可得到修正后的RNGk-ε模型，其表达方式如下式所示

2 充液直管内流场仿真

2.1 建立直管模型

图1给出充液管道模型，简化为两端简支的连续梁。运用Fluent的前处理软件GAMBIT进行直管建模，划分直管网格，设置边界条件。将GAMBIT建好的模型导入Fluent中，设定直管的初始条件选用RNGk-ε模型，设定脉动初速度为10+2sin(31.4 t)m/s。

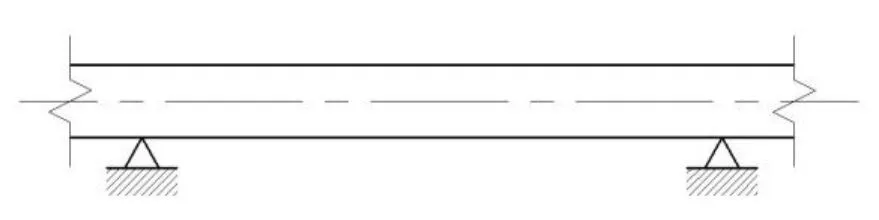
图1 充液直管结构简图Fig.1 Model of structure of fluid-filled pipe

2.2 仿真结果分析

进行直管的仿真分析，在此设脉动速度的一个周期为T，求得直管在一个周期内四个时刻的压力分布分别为0.25T、0.5T、0.75T、1T。图2是直管在初速度为波动的情况下四个时刻的压力的变化，可以看到进口处压力的变化从0.25T时刻的9 600 Pa到0.5T时刻的-24 100 Pa，再到0.75T时刻的5 500 Pa，再到1T时刻的36 600 Pa，对比这四个时刻进口的压力变化，可以发现呈现较大的波动。再对比四个时刻出口压力变化，也呈现了较大的波动。在进口周期性变化速度条件下，管内同一点的压力随着时间是不断变化的；这就说明管道内的流体在周期性入口条件下，管道内压力具有波动性，这种压力波动会引起管道的振动。

图2 充液直管四个时刻压力分布Fig.2 Pressure contour on the middle section of run pipe during four time

3 充液直管流固耦合动力学分析

3.1 ANSYSWorkbench建模

ANSYSWorkbench具有用于分析单向流固耦合的动力学模块。将Fluent中分析的直管的压力数据导入到单向耦合模块，计算管道的操作步骤如图3所示。第一步将Fluent中分析的直管的数据导入到流固耦合的模块中；第二步划分直管的网格，设计分析参数进行单向流固耦合分析。

图3 流固耦合模块图Fig.3 The module of fluid-structure coupled

3.2 计算结果分析

充液直管的管道材料选钢管其直径为200 mm，弹性模量为2.0×1011Pa，密度为7 800 kg/m3，液体密度为1000 kg/m3。管道两端简支，按支撑跨距不同，1号、2号和3号管道分别取5 m、7 m、9 m。在考虑耦合与不考虑耦合两种情况下，计算充液管道流固耦合振动的前四阶固有频率，结果列入表1。三种不同支撑间距管道的前四阶固有频率变化情况列入图4—图7中。

表1 充液直管流固耦合振动固有频率Tab.1 Inherent frequency of fluid-filled pipe

由表1可知，有耦合管道的固有频率要高于无耦合固有频率，即充液管道在考虑流固耦合作用时充液管道的频率比不考虑耦合作用时要小。1号充液管道在考虑流固耦合作用时，频率平均下降了19.82%；2号充液管道平均下降22.5%；3号充液管道平均下降26.05%。

由图4、图5和图6中可知，三种充液管道考虑流固耦合和不考虑流固耦合作用时，充液管道频率的变化。从三种充液管道频率对比来看，流固耦合作用对频率影响较大。在设计管道进行仿真时要考虑流固耦合作用的影响。

图7为考虑流固耦合作用下三种不用支持间距的频率比较图，随着支撑间距的增大，充液管道的频率逐渐降低，随着阶数的增大，频率相差逐渐增大。在设计管道时应该考虑支撑间距对充液管道的影响，设置合适的支撑间距使其避开管内液体的压力脉动的频率，以免发生共振，造成管道强烈的振动。

图4 1号管频率对比曲线Fig.4 Chart of comparative frequency of number 1 fluid-filled pipe

图5 2号管频率对比曲线Fig.5 Chart of comparative frequency of number 2 fluid-filled pipe

4 结语

充液管道的振动主要由管道结构噪声与内流压力脉动引起的，需要分析管道内的压力分布，为工程设计提供参考依据。通过ANSYSWorkbench单向流固耦合模型分析可知，流固耦合作用降低了管道的振动频率；随着管道支撑间距的增大，频率降低幅度有所增大。因此，管道系统的动态设计应考虑流固耦合的不利影响，以减小充液管道的振动危害。如果再考虑流体与结构的双向耦合，就能够提高仿真计算的精度。

图6 3号管频率对比曲线Fig.6 Chart of comparative frequency of number 3 fluid-filled pipe

图7 三种支撑间距频率对比曲线Fig.7 Chart of comparative frequency of fluid-filled pipe between three different spacing of the support

[1]沈荣瀛，胡剑凌.充液管道振动研究[J].噪声与振动控制，1996，16(5)：18-23.

[2]党锡淇，陈守五.活塞式压缩机气流脉动与管道振动M].西安：机械工业出版，1984：1-15.

[3]钱继春.高层供水系统减振降噪研究[D].天津：天津轻工业学院，2002.

[4]胡庆国.关于管道振动的分析计算及控制[J].化工建设工程，2001，(3)：42-43.

[5]苏铭德.计算流体力学基础[M].北京：清华大学出版社，1997：50-100.

[6]王福军.计算流体动力学分析CFD软件原理与应用[M].北京：清华大学出版社，2004：4-266.