居民消费价格指数的非对称性波动分析及短期预测

陈家清,张智敏,王仁祥

（武汉理工大学a.理学院；b.经济学院,武汉 430070）

0 引言

居民消费价格指数（CPI）是反映一定时期内城乡居民所购买的生活消费品价格和服务项目价格变动趋势和程度的相对数，是对城市居民消费价格指数和农村居民消费价格指数进行综合汇总计算的结果。近几个月以来，我国消费价格指数一再上涨，全国性乃至全球性通货膨胀严重，国家统计局公布：2011年1月CPI同比增涨4.9%；5月份CPI同比增长5.5%,环比上涨0.1%；6月份全国居民消费价格总水平(CPI)同比上涨6.4%。物价或许是广大市民最为关心的问题之一，因此，对居民消费价格指数的研究具有实际意义。

国内学者对CPI的分析集中在ARIMA模型和简单的ARCH模型，都没有考虑到我国CPI具有非对称性波动的特点，2011年我国居民消费价格指数波动明显存在杠杆效应。因此，本文基于我国居民消费价格指数月度数据建立组合的AR(p)非对称ARCH模型族，通过模型比较来考察CPI的波动情况，并结合所选择出的最佳模型给出短期预测以及政策建议。

1 AR(P)-ACGARCH模型

目前国内外学者为了描述时间序列群集效应，大多考虑建立自回归条件异方差（ARCH或GARCH）模型。随着研究者对具体问题的探索分析，ARCH模型不断演变发展，先后出现了许多衍生模型，如门限ARCH模型（TARCH）、指数ARCH模型（EARCH）、PARCH（Power ARCH）以及成分ARCH模型（CARCH）等一系列非对称性模型。此类非对称ARCH模型能够更合理的描述各种实际情形，对经济金融领域时间序列数据的建模分析起到了奠基性的作用。本文提出对居民消费价格指数差分序列建立组合的AR(P)非对称ARCH模型族，通过模型比较分析发现，对D_CPI序列选择建立组合的AR(p)非对称成分GARCH模型（AR(p)-Asymmetric Component GARCH，简 记 AR(p)-ACGARCH）最为合理。

1.1 AR(p)-ACGARCH模型

AR(p)-ACGARCH(1,1)模型表达式：

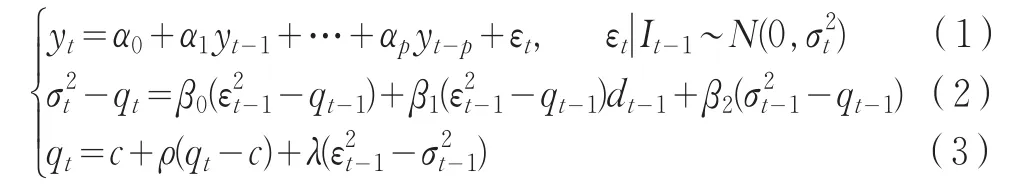
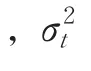
1.2 ARCH效应检验和模型估计

检验时间序列是否存在ARCH效应，最常用的方法是Engle（1984）提出的拉格朗日乘子（LM）检验和BDS检验，两种检验方法结果相似。常用的统计软件Eviews可以给出LM统计量值以及对应的p值，选定置信水平后，若统计量大于临界值（p值小于置信水平），则拒绝原假设，表示存在ARCH效应，反之亦然。

如果所研究的变量符合自回归条件异方差过程时，就可以对相关变量建立ARCH模型，由于随机扰动项εt的是异方差的，不服从古典假定，因而不能运用OLS法进行参数估计。较为常用的方法是极大似然估计（MLE），即取使得似然函数L(θ)达到最大值的对应参数θ作为参数估计值。Weiss（1984）讨论了ARMA-ARCH模型的极大似然估计，结果证明极大似然估计比OLS法更好；Bollerslev（1986）考虑了GARCH回归模型的极大似然估计；另外Hanson（1982）提出了广义矩估计（GMM）也可以对ARCH族模型进行参数估计。

2 实证分析

2.1 数据的选取和预处理

根据《中国统计年鉴》或中国经济数据库网选取1990年1月至2011年6月我国居民消费价格指数月度数据序列，记为CPIt(t=1990m01,…,2011m06)，分析我国居民消费价格指数波动情况。

首先给出我国居民消费价格指数一阶差分如图1：

图1 我国1990年1月至2011年6月居民消费价格指数一阶差分散点图

图1所示CPI一阶差分序列（即D_CPI）并没有随时间变化而呈现趋势性的变化，初略判断D_CPI序列是平稳的，下面用单位根检验结果如表1：

表1 CPI和D_CPI（一阶差分）序列ADF检验结果

由表1的单位根检验结果可知，CPI序列的t统计量大于三种置信水平的ADF临界值，而D_CPI序列的t统计量小于三种置信水平的ADF临界值，说明CPI序列是非平稳的，而D_CPI序列是平稳过程；另外D_CPI序列的自相关函数拖尾，偏自相关函数2步后截尾，因此可以考虑基于D_CPI序列建立AR(2)模型。

运用 Eviews软件分别考虑 AR(1)，AR(2)以及 AR(3)三个模型，其参数估计结果如下表2：

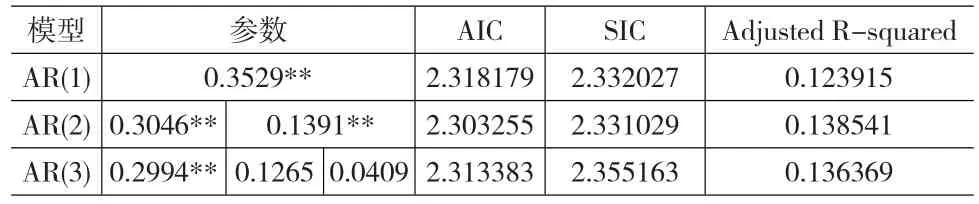
表2 对D_CPI序列分别建立AR(1)，AR(2)以及AR(3)模型的部分结果

由表2可以看出AR(2)模型的参数估计值都显著，并且AIC和SIC值最小，修正可决系数相对另外两个模型而言最大，因此建立AR(2)模型更为合理。

2.2 残差检验

通过对D_CPI建立AR(2)模型，结果似乎比较合理，然而需要进一步对残差序列进行检验，以判断残差序列是独立同分布的白噪声还是存在条件异方差。

图2 AR(2)过程残差序列散点曲线图

从图2可知，残差序列上下波动的振幅不一致，并且存在连续的正值和连续的负值，呈现出非对称性。另外通过对残差序列的自相关检验，从第8阶开始（Q(8)=7.843），随后任意阶数的Q-Stat值都显示出残差序列不服从白噪声过程。

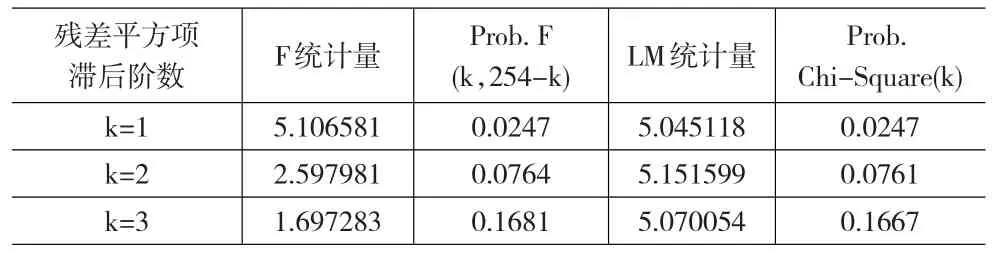
表3 D_CPI的AR(2)模型残差序列LM-ARCH效应检验结果

通过表3检验结果可知，在残差平方项滞后1阶时对应的F和LM统计量都大于5%显著水平下各个分布的临界值，对应的概率也都小于0.05，二滞后2阶或者3阶甚至是更高阶数时F和LM两个统计量检验都不显著，说明只有滞后1阶时F和LM的值都落在相应临界值的右边，原假设的拒绝域，因此判断残差序列存在一阶自回归条件异方差。

2.3 组合AR(2)非对称ARCH模型族的比较分析

鉴于图1中D_CPI序列呈现出群集效应的波动趋势（例如：1990年12月至1991年2月以及2009年1至3月连续大幅度波动，其他年月连续小幅度波动）以及残差序列存在ARCH效应的特点，为了更加精确的描述CPI月度数据序列的变化规律，本文通过非对称性检验发现D_CPI序列存在非对称杠杆效应。

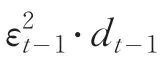
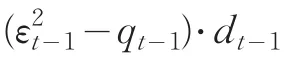
通过对以上模型比较分析得出：基于D_CPI序列建立AR(2)-TARCH、 AR(2)-TGARCH、 AR(2)-EARCH、 AR(2)-EGARCH和AR(2)-CGARCH模型时都存在参数显著为0的情形，而AR(2)-ACGARCH(1,1)模型各个参数都很显著，其他指标都正常，对数似然函数值相对另外五个模型也最大-278.734（参见表4），因此本文提出选择建立组合AR(2)-ACGARCH(1,1)模型对CPI进行模拟分析较为合理。该模型具体形式如下。

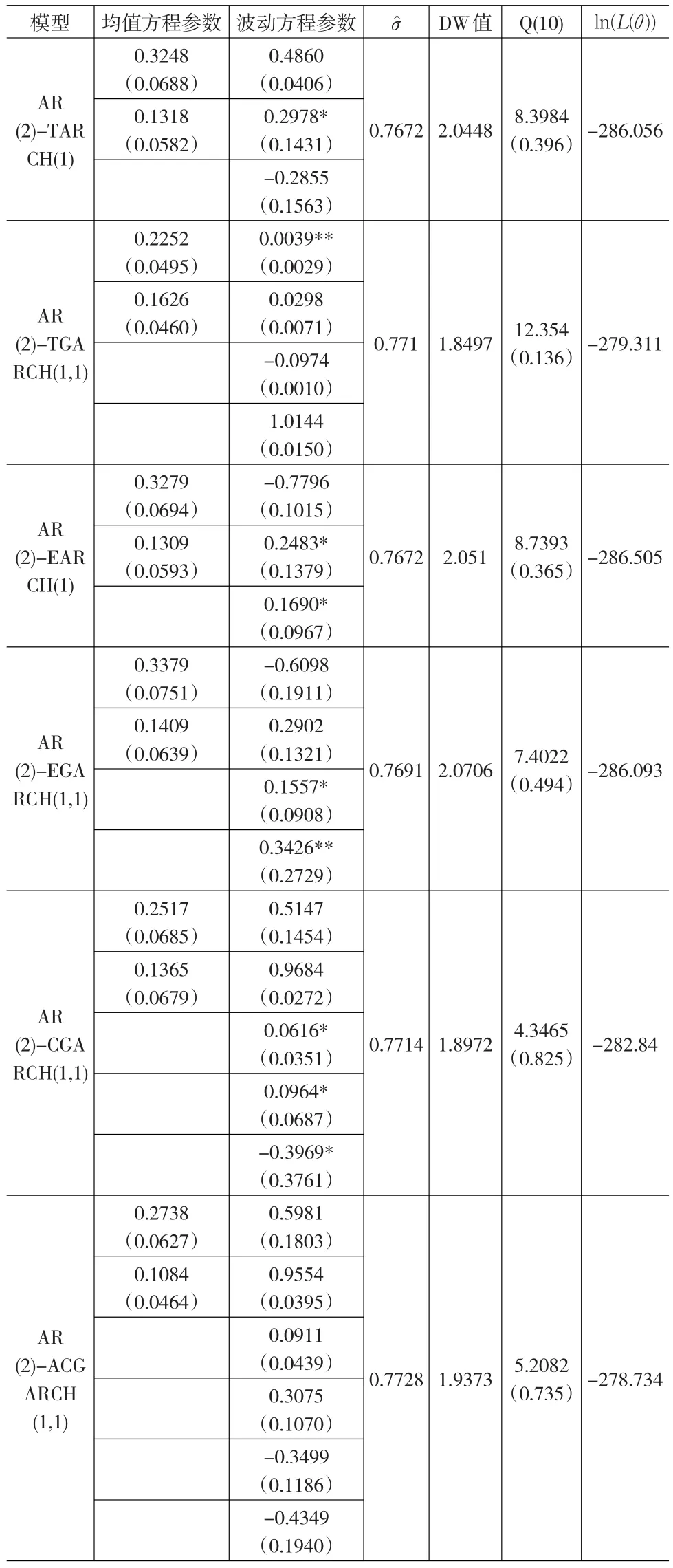
表4 基于D_CPI序列的AR(2)-非对称ARCH模型族参数估计结果

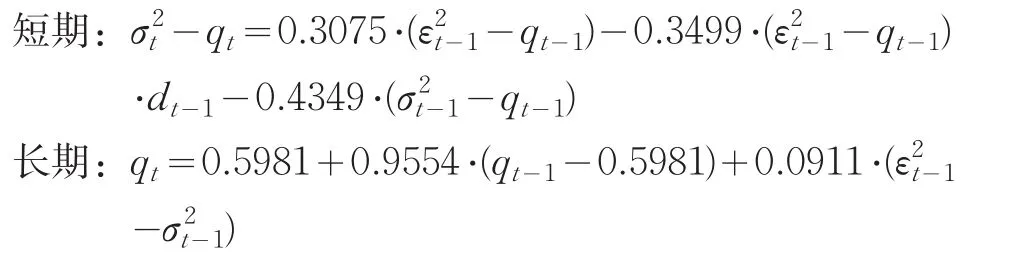
为了考察所建立的AR(2)-ACGARCH(1,1)模型是否消除了条件异方差性，本文对该模型残差序列进行了LM—ARCH检验，结果显示F和LM统计量都小于5%显著水平下各个分布的临界值，对应的概率都大于0.05，甚至滞后更高阶数时F和LM两个统计量检验都不显著，说明F和LM的值都落在相应临界值的左边（即原假设的接受域），因此判断所建立的AR(2)-ACGARCH(1,1)模型的残差项序列是白噪声，进而给出短期静态预测结果。

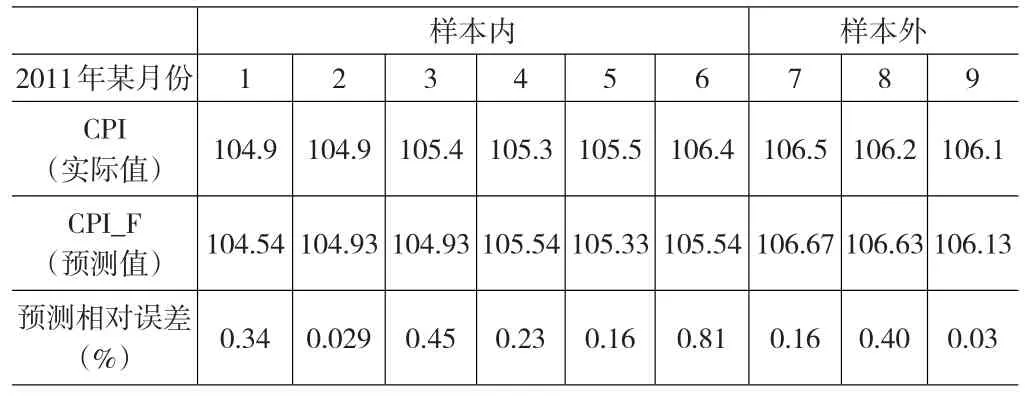
表5 基于AR(2)-ACGARCH(1,1)模型对CPI的预测结果 （上年同月100）

表5是基于AR(2)-ACGARCH(1,1)模型对我国CPI在样本内外的预测结果，其中2011年1至6月是样本内CPI的预测结果，7至9月是样本外CPI的预测结果；预测相对误差除了6月份达到0.81%（实际上，相对误差0.81%已经比较低），其他月份相对误差都低于0.5%，说明预测效果很理想；另外，样本外的预测结果显示7月份我国CPI指数约为106.67，8月份约为106.63，9月份约为106.13，即2011年第三季度我国居民消费价格指数同比上涨都将超过6%，符合当时实际情形；因此本文选择运用AR(2)-ACGARCH模型预测CPI效果相对最佳。

3 总结

本文通过对居民消费价格指数一阶差分序列进行波动性探索分析，发现D_CPI序列存在明显的非对称性群集波动特征，进而考虑建立AR(2)-TGARCH、AR(2)-EGARCH和AR(2)-ACGARCH等六种模型来分析居民消费价格指数，通过参数显著性和对数似然值等指标进行综合比较发现，选择建立AR(2)-ACGARCH模型来描述D_CPI的波动特征，并给出了短期预测结果。

短期预测结果显示在2011年第三季度（7、8和9月份）我国居民消费价格指数同比增长都将保持在6%以上，但依次呈下跌趋势；基于CPI波动的群集效应和翘尾因素的影响，预计到年底我国CPI同比增长率都不会跌回到4%以下，希望政府能够采取有效措施对价格进行有力调控，缓解进一步的膨胀压力。

[1]张世英，许启发，周红.金融时间序列分析[M].北京：清华大学出版社,2008.

[2]麻英.居民消费价格指数ARCH族模型检验[J].现代商贸工业,2011,23(3).

[3]傅俊辉,林春培,冯建勇.居民消费价格指数的波动分析[J].统计与决策,2008,(19).

[4]陈昊.基于不对称自回归条件异方差模型的短期负荷预测[J].电网技术业,2008,32(15).

[5]D.Giannikis,I.D.Vrontos,P.Dellaportas.Modelling Nonlinearities and Heavy Tails Via Threshold Normal Mixture GARCH Models[J].Computational Statistics&Data Analysis,2008,(52).

[6]Alexander,C.,Lazar,E.Normal Mixture GARCH(1,1)：Applications to Exchange Rate Modeling[J].J.Appl.Econometrics,2006,21.

[7]S.Y.Hwang,I.V.Basawa.Stationarity and Moment Structure for Box-Cox Transformed Threshold GARCH(1,1)Process[J].Statistics&Probability Letters,2004,(68).

[8]E.Goncalves,N.Mendes-Lopes.On the Structure of Generalized Threshold arch Processes[J].Statistics and Probability Letters,2010,(80).

[9]J.Liu,W.K.Li,C.W.Li.On a Threshold Autoregression with Condi⁃tional Heteroscedastic Variances[J].Journal of Statistical Planning and Inference,1997,(15).