Ground states for asymptotically periodic quasilinearSchrödinger equations with critical growth

Zhang Hui Zhang Fubao

(Department of Mathematics, Southeast University, Nanjing 211189, China)

1 Introduction and Statement of Main Result

As the models of physical phenomena, the quasilinear Schrödinger equation

(1)

has been extensively studied in recent years. For the detailed physical applications, one can see Ref.[1].

Inspired by Refs.[4-5], we are interested in the existence of ground states for asymptotically periodic quasilinear Schrödinger equation (1). We consider

-Δu+V(x)u-uΔ(u2)=K(x)|u|22*-2u+g(x,u)

u∈H1(RN)

(2)

LetFbe a class of functionsh∈C(RN)∩L∞(RN), such that for every>0 the set {x∈RN:|h(x)|≥} has a finite Lebesgue measure. Suppose thatV,K∈C(RN) satisfies the following conditions:

H1) There exists a constanta0>0 and a functionVp∈C(RN), 1-periodic inxi, 1≤i≤N, such thatV-Vp∈FandVp(x)≥V(x)≥a0,x∈RN.

H2) There exists a functionKp∈C(RN), 1-periodic inxi, 1≤i≤N, and a pointx0∈RNsuch thatK-Kp∈Fand

①K(x)≥Kp(x)>0,x∈RN;

②K(x)=|K|∞+O(|x-x0|N-2), asx→x0.

H3)g(x,u)=o(u) uniformly inxasu→0;

H4) |g(x,u)|≤a(1+|u|q-1), for somea>0 and 4≤q<22*;

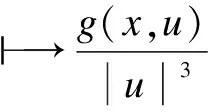
H6) There exists a neighborhood ofx0given by H2),Ω⊆RN, such that

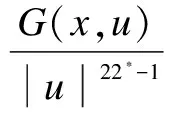
H7) There exists a constantq1∈(2,22*), functionsh∈Fandgp∈C(RN×R,R) such that

①gpis 1-periodic inxi,1≤i≤N;

② |g(x,u)-gp(x,u)|≤|h(x)|(|u|+|u|q1-1),x∈RN;

Theorem1If H1) to H7) hold, then the problem (2) has a ground state.

Remark1H3) and H5) imply that

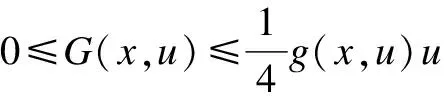
(3)

2 Variational Setting

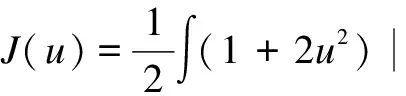
is not well defined inH1(RN). Choose the changefdefined by

f(t)=-f(-t) on (-∞,0]

and setv=f-1(u), then we obtain

which is well defined inH1(RN) by the properties off(see Ref.[5]). The critical points ofIare weak solutions of

-Δv+V(x)f′(v)f(v)=K(x)|f(v)|22*-2f(v)f′(v)+g(x,f(v))f′(v)v∈H1(RN)

(4)

Similar to Ref.[5], we first prove that there is a nontrivial solution for Eq.(4). We know that the results obtained under (V), (K), (g1), (g2) and (g5) in Ref.[5] still hold since the conditions H1) to H4) and H6) are the same as (V), (K), (g1), (g2) and (g5), respectively. However, H5) and H7) are different from (g3) and (g4) in Ref.[5]; in the following, we verify whether the results under (g3) and (g4) still hold.

Lemma1Let H1) to H5) hold. Then, the (Ce)b(b>0) sequencevnofIsatisfying

I(vn)→b, =I′(vn)=(1+=vn=)→0

(5)

is bounded.

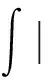
By (5), we have

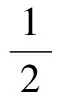
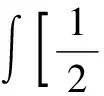
I1+I2+I3

(6)

By Lemma 1 (8) in Ref.[5], we obtain

(7)

ForI3, using Lemma 1 (8) in Ref.[5] and inequality (3), we have

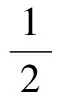
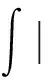
In Ref.[5], the authors supposed that |g(x,u)-gp(x,u)|≤h(x)|u|q3-1,q3∈[2,22*), and we assume that |g(x,u)-gp(x,u)|≤h(x)(|u|+|u|q1-1),q1∈(2,22*). So Lemma 9 in Ref.[5] holds under H1), H2) and H7). Following the outline in Ref.[5], we have the following lemma.

In order to find ground states, we also need to introduce the Nehari manifold. The Nehari manifold corresponding to Eq.(4) is

M={u∈H1(RN){0}: 〈I′(u),u〉=0}

First, we give the following lemma in which the simple proof is left to the reader.

Lemma3Let H1) to H5) hold. ThenI(tu)→-∞ ast→∞,u∈H1(RN){0}.

Inspired by Ref.[6], we have

Note that

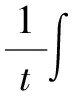
t(|v+Φ1(t)+Φ2(t)+Φ3(t))

By Lemma 1 (8) in Ref.[5] and the fact thatf″(tv)=-2f(tv)f′4(tv), we obtain

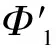
2f2(tv)f′4(tv)tv2-f(tv)f′(tv)v]V(x)<0

SoΦ1is decreasing.

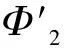
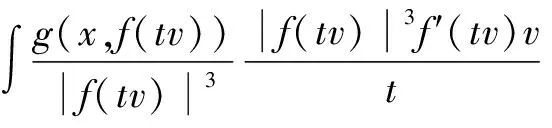
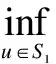
(8)

Lemma5Let H1) to H6) hold. Thenc*≥c.

3 Proof of Theorem 1

ProofBy Lemma 2, we assume that there is a nontrivial solutionwwithI(w)=c. Thenw∈M. SoI(w)≥c*. Note thatI(w)=candc*≥c, and we obtainI(w)≤c*. SoI(w)=c*. Then we can easily infer thatwis a ground state for Eq.(4). We complete the proof.

[1]Kurihara S. Large-amplitude quasi-solitons in superfluid films [J].JournalofthePhysicalSocietyofJapan, 1981,50(10): 3262-3267.

[2]Liu J, Wang Z. Soliton solutions for quasilinear Schrödinger equations Ⅰ [J].ProceedingsoftheAmericanMathematicalSociety, 2003,131(2): 441-448.

[3]Liu J, Wang Y, Wang Z. Solutions for quasilinear Schrödinger equations via the Nehari method [J].CommunicationsinPartialDifferentialEquations, 2004,29(5/6): 879-901.

[4]Liu X, Liu J, Wang Z. Ground states for quasilinear Schrödinger equation with critical growth [J].CalculusofVariationsandPartialDifferentialEquations, 2013,46(3/4): 641-669.

[5]Silva E A B, Vieira G F. Quasilinear asymptotically periodic elliptic equations with critical growth [J].CalculusofVariationsandPartialDifferentialEquations, 2012,39(1/2): 1-33.

[6]Szulkin A, Weth T. The method of Nehari manifold [C]//HandbookofNonconvexAnalysisandApplications. Boston, USA: International Press, 2010: 597-632.

[7]Do J M, Miyagaki O H, Soares S H M. Soliton solutions for quasilinear Schrödinger equations with critical growth [J].JournalofDifferentialEquations, 2010,248(4): 722-744.

[8]Silva E A B, Vieira G F. Quasilinear asymptotically periodic Schrödinger equations with subcritical growth [J].NonlinearAnalysis:Theory,MethodsandApplications, 2010,72(6): 2935-2949.