开关磁阻电机改进型简化磁链无位置传感器技术
张磊, 刘闯, 王云林, 张云龙
(南京航空航天大学自动化学院,江苏南京 210016)
开关磁阻电机改进型简化磁链无位置传感器技术
张磊, 刘闯, 王云林, 张云龙
(南京航空航天大学自动化学院,江苏南京 210016)
针对简化磁链方法只能实现单相轮流导通,不利于电机出力的问题,提出一种基于特征位置磁链的改进型简化磁链开关磁阻电机位置估计方法。根据电感、转子位置、磁链三者之间的关系,以电感曲线的交点为特征位置,用实时计算得到的磁链与特征位置磁链比较获取转子位置信号。为更进一步简化位置估计算法,提出一种五点法磁链优化模型来自动生成特征位置磁链方法,并通过理论仿真分析,对五点法磁链模型进行了优化设计,该方法省去了实测磁链和创建磁链数据表的繁琐过程。实验结果验证了该方法的正确性和可行性。
开关磁阻电机;无位置;五点法磁链优化模型;特征磁链;改进型简化磁链
0 引言
开关磁阻电机(switched reluctance machine,SRM)为双凸极定转子结构,转子没有线圈,结构简单坚固、成本低、调速范围宽、控制灵活、适应高温、高速及恶劣环境等优点,适用于航空、电动汽车等领域。但SRM需要位置传感器来确定转子的位置信号,这既增加了系统的成本也增加了系统的复杂程度,同时也不适应在潮湿、振动、多尘等恶劣环境场合。因此研究无位置传感器技术已成为SRM领域的热点。
目前国内外学者对SRM无位置传感器技术做了大量研究,提出了多种位置估计方案。如脉冲注入法[1-3],电感模型法[4-5]、模型观测器法[6-9],磁链电流法[10-14]等。文献[10 -14]采用磁链电流法检测位置信号。其中文献[10]提出双开关磁阻电机磁链模型无传感器位置技术。文献[11]利用磁链-电流-转子位置间的关系实现位置估计,需离线获取磁链数据,建立三维数据表。文献[12]在文献[11]的基础上进行了简化,选定最大位置附近作换相时刻,通过实时计算磁链与换相位置磁链比较得到估计的位置,该方法只需二维数据,所需内存小。文献[13]又在文献[12]基础上把能量优化开关角与简化磁链的方法相结合。文献[14]提出任意给定开通角且与关断角无关的改进型磁链法,有利于在进行无位置传感器控制的同时实现效率优化和转矩脉动最小化等要求。
本文在文献[12-14]基础上对简化磁链方法进一步改进,提出基于特征位置的特征磁链自动生成的改进型简化磁链方法。该方法不需要实测磁链,不需要创建磁链数据表,节省内存,算法简单,省去查表的环节,提高了微处理器的实时性,同时可以实现电机的双拍起动,提高电机的起动效果。特征位置磁链采用五点法磁链优化模型自动生成,并对五点法磁链优化模型进行仿真和实验对比。以此搭建了SRM位置估计的实验平台,进行了位置估计的实验验证。
1 改进型简化磁链位置估计原理
本文以12/8结构SRM为研究对象,图1为A、B、C 三相电感(LA,LB,LC)与转子位置(P,Q,R)之间的关系。转子齿距角为45°,每一步的角位移为15°,B相的转子位置信号滞后A相15°,C相的转子位置信号滞后B相15°,A相的转子位置信号滞后C相15°。A相7.5°对应C相位置信号的下降沿,A相15°对应B相位置信号的上升沿;同理,B相7.5°对应A相位置信号的下降沿,B相15°对应C相位置信号的上升沿;C相7.5°时对应B相位置信号的下降沿,C相15°时对应A相位置信号的上升沿。
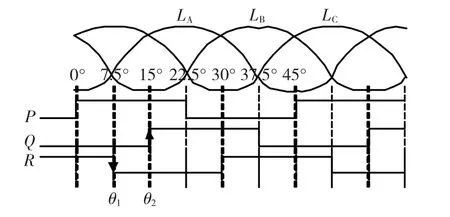
图1 三相电感与转子位置关系Fig.1 The relation of the inductance and position
所以,转子7.5°与15°位置是两个特殊的位置,根据磁链-电流-位置间关系,以这两个特殊位置磁链作为特征磁链,将实时磁链与特征磁链比较就可以得到对应相的位置信号边沿时刻。为了算法的简便,本文将该方法进一步改进,只将7.5°特征位置作为换相位置,作为位置估计的基准,而15°特征位置由7.5°位置根据实时转速延时得到。该方法与文献[13-15]比较优点是7.5°位置的磁链密度比最大位置附近磁链密度小,微处理器在处理7.5°位置磁链时实时性和精度都要高,并且可是实现双拍起动。
改进型简化磁链位置估计过程是:采集A相绕组的电压、电流,通过积分运算得到实时磁链,将实时磁链值与7.5°位置的特征磁链比较,如果实时磁链值大于同电流下的7.5°位置特征磁链,就关断C相,再根据实时转速将A相延迟7.5°得到A相的15°特征位置,开通B相;同理,比较B相实时磁链与B相7.5°特征磁链得到A相的关断信号,延迟7.5°得到C相的开通信号;比较C相实时磁链与C相的7.5°特征磁链得到B相关断信号,延迟7.5°得到A相开通信号。其位置估计结构图如图2所示,7.5°特征磁链由五点法磁链优化模型自动生成,该模型在后面讲解。
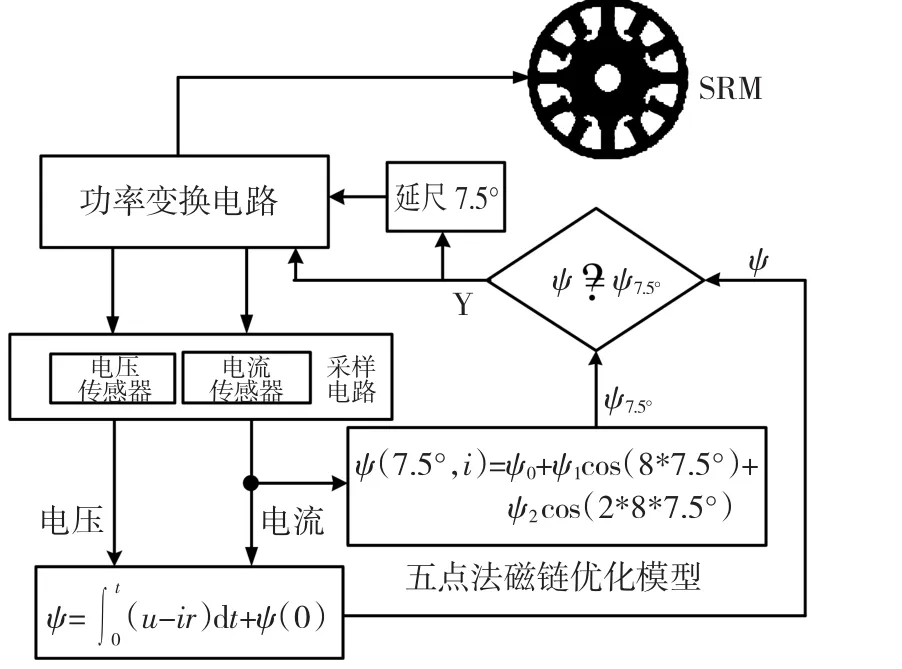
图2 改进型简化磁链位置估计结构图Fig.2 Block diagram for the position estimation
2 特征磁链的自动生成
2.1 五点法磁链模型
传统简化磁链方法换相位置磁链需要实测,过程繁琐,且占用内存。本文采用五点法磁链优化模型自动生成得到。
文献[15-16]对五点法磁链模型进行了一些讨论,但没有研究如何将该磁链模型应用到无位置传感器技术中。
将SRM的相电感模型用傅里叶级数近似逼近,再在展开式两边乘以电流,即可得到磁链模型为
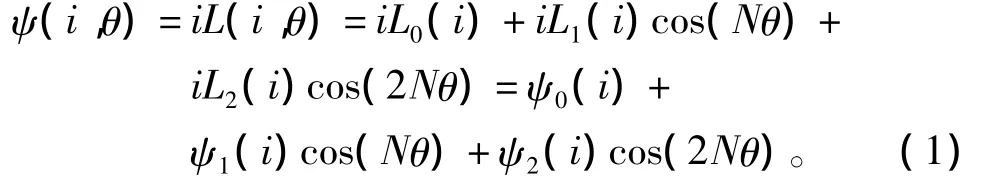
其中:系数N 是SRM 的转子数;系数 ψ0、ψ1、ψ2是对齐位置磁链ψa,非对齐位置磁链ψu,中间位置磁链ψm的关系表达式,所以只要计算出这3个位置上的磁链就可以确定系数 ψ0、ψ1、ψ2。
忽略饱和与磁滞效应,非对齐位置磁链可以用一条直线表示为

对齐位置和中间位置磁化曲线与反正切函数相似,所以可以通过反正切函数拟合为

式(3)和式(4)中的 a1、a2、m1、m2是待定的常数。可以在中间和对齐位置磁化曲线上分别选取2个点,由4个点位置的磁链、电流就可以求得a1、a2、m1、m24个待定常数,再在非对齐位置磁化曲线上选取一个点,5个点就可以将式(1)中的系数ψ0、ψ1、ψ2确定。
2.2 五点法磁链模型优化
图3是5个点的位置,非对齐位置磁链曲线是一条直线,所以可以任选一个点位置,齐位置和中间位置磁化曲线上在刚饱和位置附近选取2个点,对应的电流为IS,另外2个点选在电流IS(3~4倍)位置。
磁链饱和是一个渐进的过程,如何确定饱和附近两个点位置是影响整个五点法磁链模型精度的关键,文献[15-16]没有作进一步研究。针对这种现象,本文通过对饱和附近两个点的电流(IS)进行优化仿真,分析基于不同IS的五点法磁链模型相对误差大小,以获取五点法磁链优化模型。
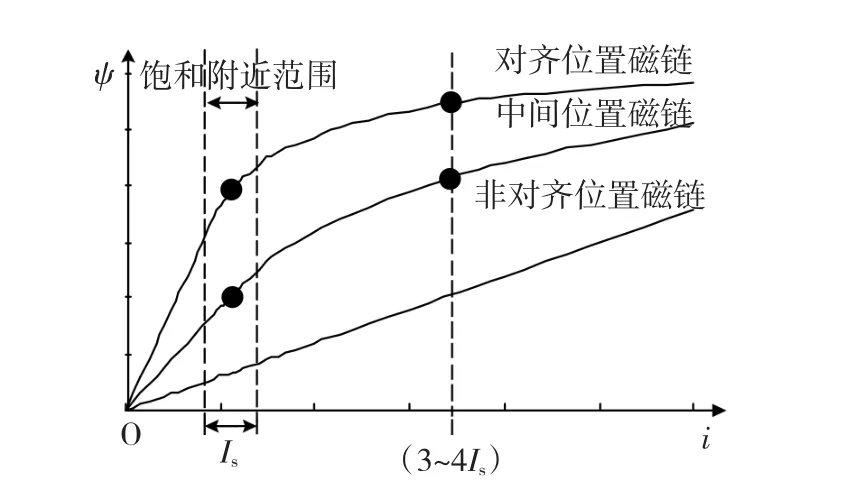
图3 磁链曲线与五点位置关系Fig.3 The relation of the flux linkage and five dot
由于 IS的选取不同,计算出来的 a1、a2、m1、m2系数也就不同,得到的五点法磁链模型就不同,所以不同IS对应的五点法磁链模型拟合出的磁化曲线与有限元计算的磁化曲线的相对误差也就不同。根据样机有限元计算,磁化曲线饱和电流在5.5 A附近,分别取IS在3~7 A范围内对磁链模型进行优化分析,表1是在对齐、中间和非对齐位置下,不同IS的五点法磁链模型拟合的磁链曲线与有限元磁化曲线的相对误差,图4是在任意角度下,不同IS的五点法磁链模型拟合的磁链曲线与有限元磁化曲线的相对误差,从表1和图4的优化仿真综合分析,当IS在5 A时,五点法磁链模型拟合的磁链相对误差最小,因此本实验选取IS为5 A作为选取五个点的基准。
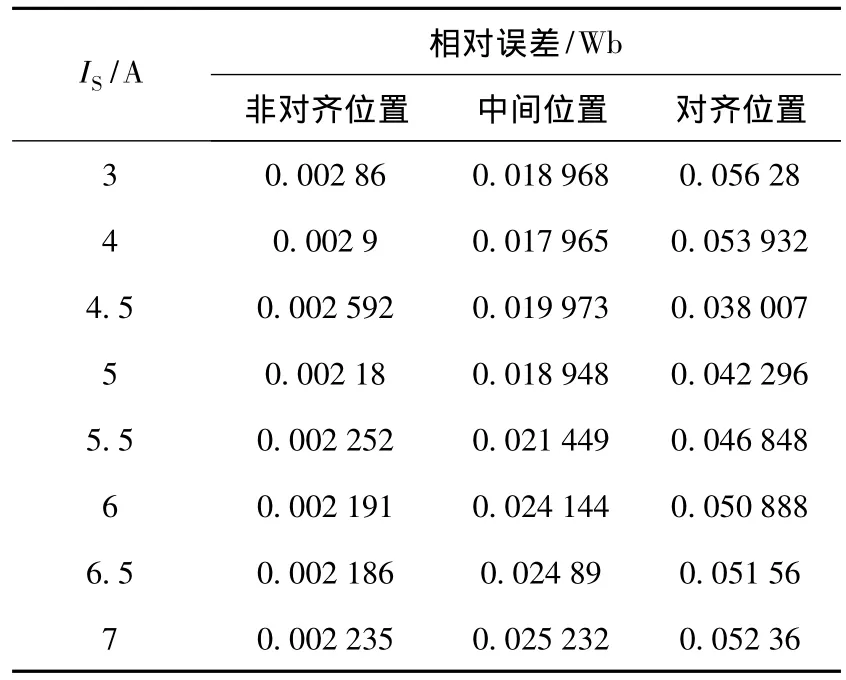
表1 IS不同取值的优化表Table 1 Optimize table of the different IS
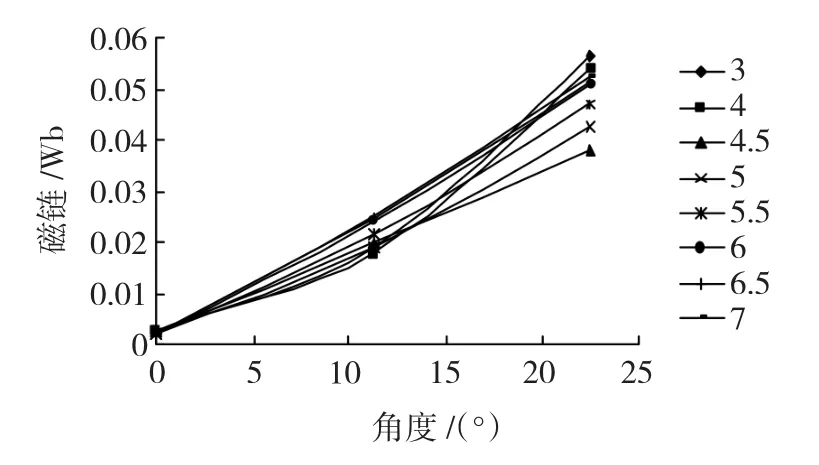
图4 不同IS、不同位置下的相对拟合误差Fig.4 Relative error of the different IS
根据前面的优化仿真,5个点位置分别选取非对齐位置磁链曲线上(10 A,0.001 192 4 Wb),中间位置磁链曲线上两个点是(5 A,0.018 541 5 Wb)、(20 A,0.044 237 5 Wb),对齐位置磁链曲线上的两个点是(5 A,0.036738 Wb)、(20 A,0.055906 Wb),如图5所示。
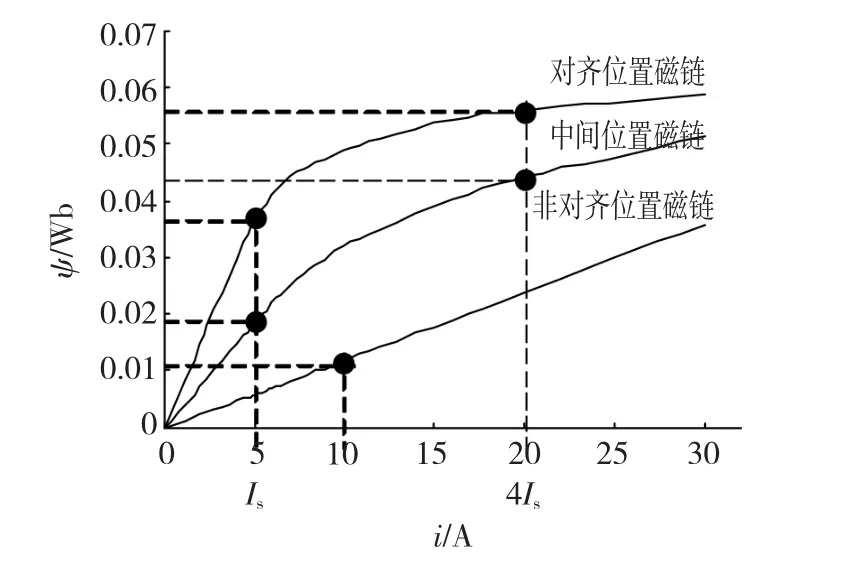
图5 五点法磁链优化模型五点位置Fig.5 The five dot position of the optimize model
由五个点位置的磁链、电流解算出式(3)、式(4)中的待定系数 a1、a2、m1、m2,进而得到对齐位置(ψa)、中间位置(ψm)、非对齐位置(ψu)磁链曲线解析表达式(5),因为 ψ0、ψ1、ψ2是 ψa、ψm、ψu的关系表达式,所以容易得到式(1)的五点法磁链优化模型。图6是五点法磁链优化模型分别拟合出的对齐位置、中间位置、非对齐位置不同角度下的磁化曲线与有限元磁化曲线的对比图。其中ψ^a是五点法磁链优化模型计算的对齐位置磁链,ψ^u是五点法磁链优化模型计算的非对齐位置磁链,ψ^m是五点法磁链优化模型计算的中间位置磁链。从仿真对比看出只有在对齐位置非饱和区磁链误差稍微大些,其他角度位置误差都很小,由此说明,五点法优化磁链模型能够很好的反应电机的磁链特性。

本文所提的基于7.5°位置磁链的改进型简化磁链位置估计方案中,7.5°位置的特征磁链由五点法磁链优化模型得到。五点法磁链优化模型是磁链ψ、角度θ、电流i的数学关系式,由于7.5°特征位置角度是固定的,所以7.5°特征磁链只需电流值即可自动生成,不需要实测7.5°特征磁链,也不需要创建磁链数据表,不需要查表,从而提高了处理器的实时性和位置估计的精确度。
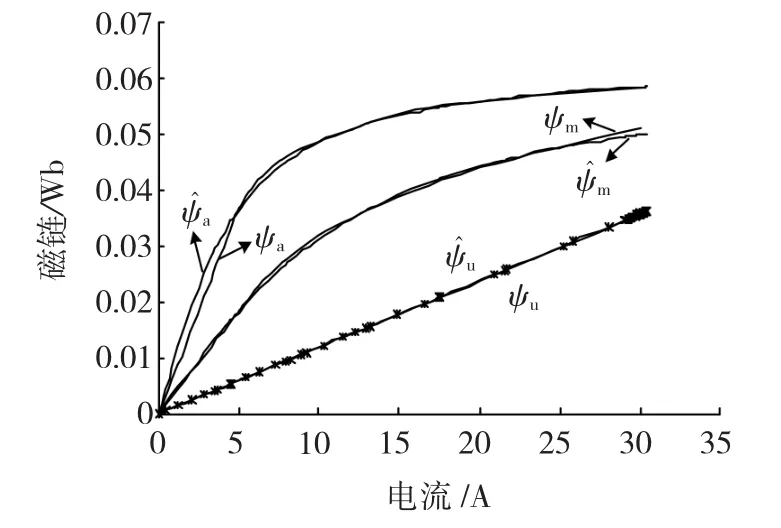
图6 非对齐、中间、对齐位置磁化曲线对比Fig.6 The comparison for the flux linkage of the three position
3 振动和噪声对位置估计的影响
振动与噪声是开关磁阻电机的缺点,它影响到电流、电压的采集,所以在磁链/电流型的无位置传感器方法中,振动与噪声会影响到位置估计的精确度,本文利用随机函数构建一个振动噪声源,通过仿真,分析不同程度的振动与噪声对位置估计的影响。图7是在振动与噪声影响下,电流和电压发生±20%范围内误差时,电流、电压、7.5°特征磁链的波形图。
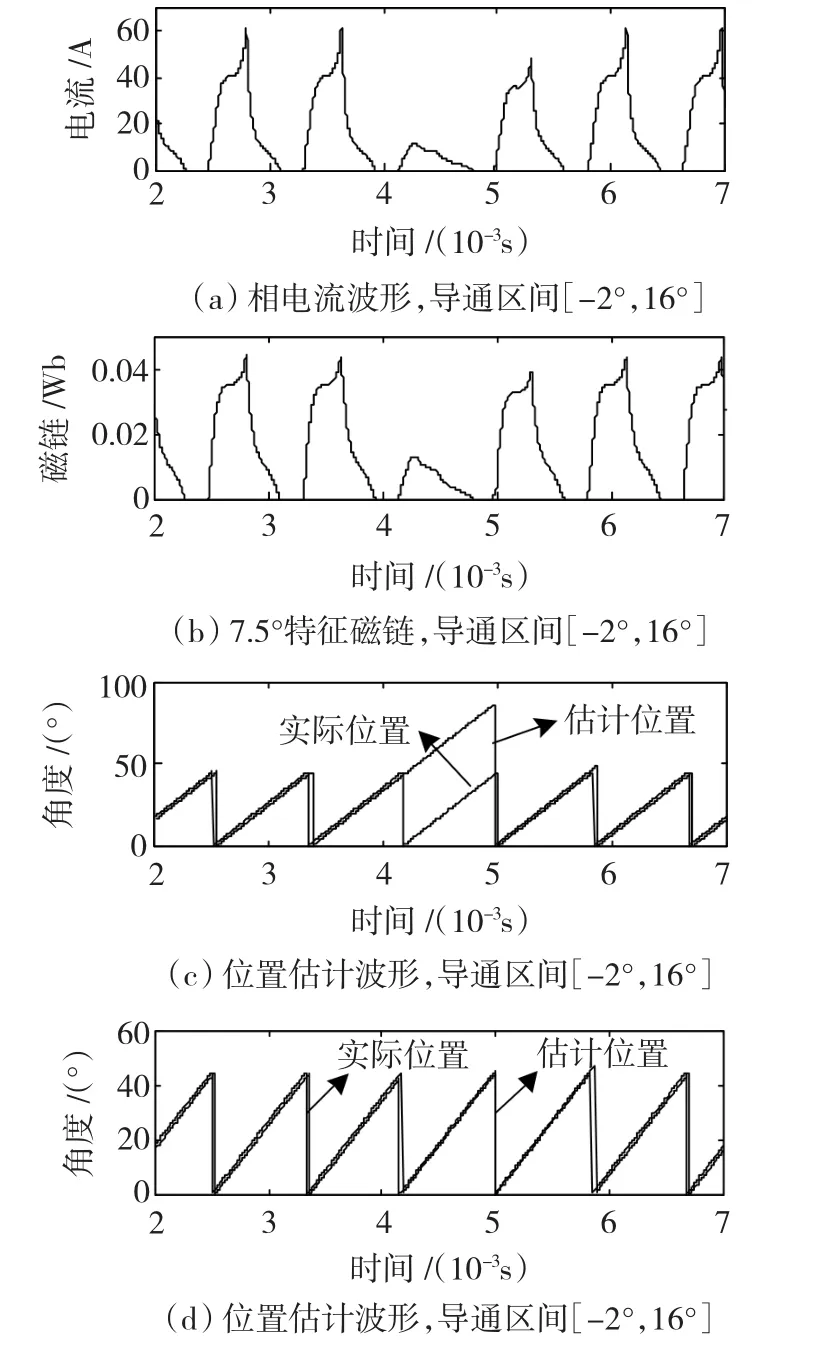
图7 不同振动与噪声下电流/磁链/位置估计波形Fig.7 The waveform of the phase current,flux linkage and estimated position at the different noise and vibrancy
由图7(a)看出因为振动与噪声的干扰,在4~5 ms之间采集的电流误差很大,根据ψ=LI,所以7.5°特征磁链在4~5 ms之间变化也是很大(图7(b)所示),这样最终导致估计出来的位置信号在4~5 ms误差也变得很大(图7(c)所示)。当振动与噪声减小时,位置估计误差也就减小,图7(d)是在振动与噪声影响下,电流和电压产生±10%范围内误差时,位置估计波形图,位置估计误差减小了,由此看出,振动与噪声等干扰信号对位置估计的精度有直接的影响。
4 实验验证
4.1 五点法磁链优化模型验证
为进一步验证该磁链优化模型的可行性,通过实验和仿真对样机的动态磁链进行对比分析。图8是基于五点法磁链优化模型的动态磁链仿真,图8(a)是实时动态磁链,图8(b)图是特征位置7.5°的动态特征磁链。根据 ψ=Li,电感 L不变,所以7.5°动态磁链与相电流成正比关系,其动态磁链波形与电流波形相似,在关断角时刻动态磁链值约为0.048 Wb,7.5°特征磁链在电流最大时为0.02 Wb。图9是五点法磁链优化模型实验得到的动态磁链,从实验结果看出样机的动态磁链在关断角时刻约为0.046 Wb,7.5°动态特征磁链在电流最大时约为0.023 Wb,与仿真的结果相差不大,从而验证了五点法磁链优化模型的可行性。

图8 五点法磁链优化模型仿真计算的磁链Fig.8 The flux linkage simulation based on the optimize model
由于五点法磁链优化模型不存在积分累计误差,所以基于五点法磁链优化模型的改进型简化磁链位置估计精度会得到更进一步的提高。
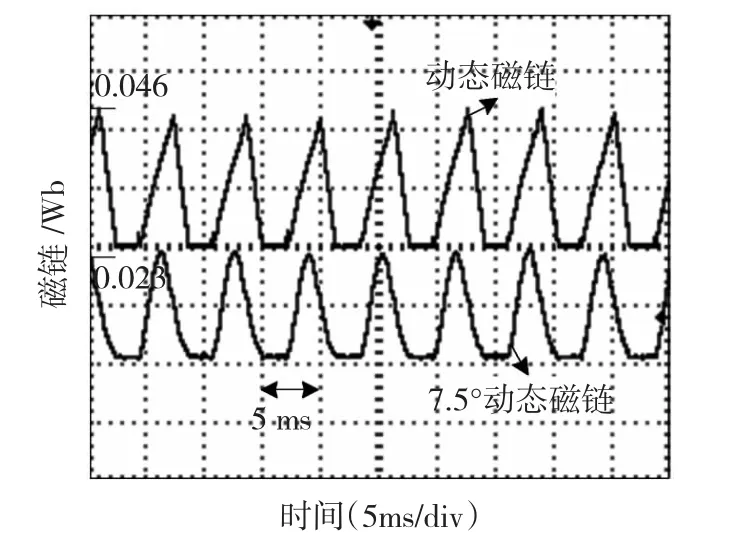
图9 五点法磁链优化模型实验的磁链Fig.9 The experiment for the flux linkage based on the optimize model
4.2 空载位置估计实验
图10是空载不同转速情况下位置估计的实验,其中,转速为850 r/min时,估计的位置与实际位置相差350 μs,相差的角度为 2.97°;转速在 2 000 r/min时,估计的位置与实际位置相差100 μs,相差的角度为2°。图11是不同转速下估计位置与实际位置之间的误差曲线,可以看出,随着转速的提高,误差减小,说明磁链法无位置传感器技术适合在中、高速运行情况下。

图10 空载不同转速下位置估计和相电流Fig.10 The estimated position and phase current of the different speed for the B phase

图11 不同转速下估计的位置角度误差Fig.11 The error of the estimated angle at different speed
4.3 带载位置估计实验
图12为电流斩波限为2 A,负载分别为0.54 N·m和0.36 N·m,不同转速下的估计位置和相电流波形,从实验结果看出,在负载情况下,基于五点法磁链优化模型的改进型简化磁链估计的位置信号与实际位置信号误差很小,说明在加载斩波控制运行中该位置估计算法也同样具有很高的精确度。
实验中估计的位置信号和位置传感器得到位置信号相同,都是1/2周期导通的位置信号,所以能够实现双拍运行,与传统的简化磁链方法得到的位置信号只能实现单拍运行不同,所以改进型简化磁链位置估计方法能提高SRM的电动效率。

图12 不同负载下位置估计及相电流Fig.12 The estimated position and the phase current
5 结论
本文在SRM五点法磁链模型进行优化分析的基础上,提出一种基于7.5°特征磁链方法的改进型简化磁链无位置传感器技术。
(1)该方法无需增加系统的硬件资源,算法简单,不需要实测磁链,可适应不同定转子结构的开关磁阻电机,具有很强的通用性。
(2)分析了SRM五点法磁链模型,并对其进行优化仿真,得出五点法磁链优化模型,并将此模型应用到无位置传感器技术中。
(3)建立了基于dSPACE的位置估计平台,通过在一台三相12/8的SRM样机上的实验,验证了所提的位置估计方法的有效性和正确性。
[1] 李景男,王旭东.基于两相脉冲激励的开关磁阻电动机的无位置传感器转子位置检测[J].电机与控制学报,2002,6(1):6-9.
LI Jingnan,WANG Xudong.Sensorless rotor position detection of SRM based on voltage pulses to two phases[J].Electric Machines and Control,2002,6(1):6 -9.
[2] KAYIKCI E,HARKE M C,LORENZ R D.Load invariant sensorless control of a switched reluctance drive using high frequency signal injection[C]//Industry Applications Conference,39th IAS Annual Meeting,October 3 - 7,2004,Seattle,USA.2004:1632-1637.
[3] ZHANG Lei,LIU Chuang,ZHU Shushu,et al.Eigenvalue detection method for SRM rotor position estimation[C]//In Proc.ICEMS’11,August 20 -23,2011,Bijing,China.2011:1 -5.
[4] 陈坤华,孙玉坤,吴建兵,等.基于电感模型的开关磁阻电机无位置传感技术[J].电 工 技 术 学 报,2006,21(11):71-75.
CHEN Kunhua,SUN Yukun,WU Jianbing,et al.Inductance model-based sensorless control of the switched reluctance motors[J].Transactions of China Electrotechnical Society,2006,21(11):71-75.
[5] GAO Hongwei,FARZAD Rajaei,Salmasi,et al.Inductance model-based sensorless control of the switched reluctance motor drive at low speed[J].IEEE Transactions on Power Electronics,2004,19(2):1568-1573.
[6] CHEOK A D,ERTUGRUL N.High robustness and reliability of fuzzy logic based postion estimation for sensorless switched reluctance motor drives[J].IEEE Transactions on Power Electronics,2000,15(2):319 -334.
[7] NESIMI E,CHEOK A D.Indirect angle estimation in switched reluctance motor drives using fuzzy logic based motor model[J].IEEE Transactions on Power Electronics,2000,15(6):1029-1044.
[8] 夏长亮,王明超,史婷娜,等.基于神经网络的开关磁阻电机无位置传感器控制[J].中国电机工程学报,2005,25(13):123-128.
XIA Changliang,WANG Mingchao,SHI Tingna,et al.Position sensorless control for switched reluctancemotors using neural net-work[J].Proceedings of the CSEE,2005,25(13):123 -128.
[9] 夏长亮,谢细明,史婷娜.开关磁阻电机小波神经网络无位置传感器控制[J].电工技术学报,2008,23(7):33-38.
XIA Changliang,XIE Ximing,SHI Tingna.Position sensorless control of switched reluctance motor using wavelet neural networks[J].Transactions of China Electrotechnical Society,2008,23(7):33-38.
[10] 张旭隆,谭国俊,王其虎.磁链模型的双开关磁阻电机无位置传感器控制[J].电机与控制学报,2011,11(15):55 -60.
ZHANG XuLong,TAN Guojun,WANG Qihu.Sensorless control of double switched reluctance motor based on flux model[J].E-lectric Machines and Control,2011,11(15):55 -60.
[11] GABRIEL Gallegos Lopez.High grade position estimation for SRM drives using flux linkage/current correction model[J].IEEE Transactions on IA,1998,34(4):859 -869.
[12] 邱亦慧,詹琼华,马志源.基于简化磁链法的开关磁阻电机间接位置检测[J].中国电机工程学报,2001,21(10):59-62.
QIU Yihui,ZHAN Qionghua,MA Zhiyuan.The indirect position sensing of SRM on the basis of simplified flux method[J].Proceedings of the CSEE,2001,21(10):59-62.
[13] 郑洪涛,蒋静坪,徐德鸿,等.开关磁阻电动机无位置传感器能量优化控制[J].中 国 电 机 工 程 学 报,2004,24(1):153-157.
ZHENG Hongtao,JIANG Jingping,XU Dehong,et al.Switched reluctance motor sensorless drive with energy optimizing control strategy strategy[J].Proceedings of the CSEE,2004,24(1):153-157.
[14] 李珍国,李彩红,阚志忠,等.基于改进型简化磁链法的开关磁阻电机无位置传感器速度控制[J].电 工 技 术 学 报,2011,26(6):62 -66.
LI Zhenguo,LI Caihong,KAN Zhizhong,et al.Switched reluctance motor sensorless speed control based on the improved simplified flux method[J].Transactions of China Electrotechnical Society,2011,26(6):62 -66.
[15] CHI H P,LIN R L,CHEN J F.Simplified flux-linkage model for switched-reluctance motors[J].IEE Proceedings of Electric Power Applications,2005,152(3):577 -583.
[16] 杨岳峰,张奕黄,王素杰,等.基于简化磁链模型的SRG自励发电[J].电 工 技 术 学 报 2009,24(1):61-64.
YANG Yuefeng,ZHANG Yihuan,WANG Sujie,et al.Self-excited SRG based on simplified flux-linkage model[J].Transactions of China Electrotechnical Society,2009,24(1):61 -64.
(编辑:刘琳琳)
Sensorless technology of switched reluctance motor based on the improved simplified flux method
ZHANG Lei, LIU Chuang, WANG Yun-lin, ZHANG Yun-long
(College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
The conventional simplified flux linkage sensorless only realizes single phase alternate conducting,and the output power efficiency of the motor is low.As a result,an improved simplified flux linkage sensorless method of switched reluctance motor based on the special position flux is proposed in this paper.Based on the analysis of the relationship among phase inductance and the rotor position and flux linkage,the special position is the intersecting of the phase inductance curve.The position signal was estimated by means of the real-time flux linkage compared with the special position flux linkage.To increase the accuracy of the estimate position,the special position flux linkage was automatically created based on the five dot optimization of flux model,omitting the process of the flux linkage detection and look-up table in the memory.Through theoretic analysis,simulation and experiment,it proves the validity and feasibility of the improved simplified flux linkage sensorless method and the five dot optimization of flux model.
switched reluctance motors;sensorless;five dot optimization of flux model;special flux;improved simplified flux linkage
TM 352
A
1007-449X(2013)11-0013-07
2013-03-31
国家自然科学基金(51377076);江苏省"六大人才高峰"资助项目(50977044)
张 磊(1974—),男,博士研究生,副教授,研究方向为开关磁阻电机无位置传感器技术;
刘 闯(1973—),男,博士,教授,博士生导师,研究方向为特种电机及控制、新能源技术;
王云林(1989—),女,硕士研究生,研究方向为混合动力汽车驱动系统;
张云龙(1989—),男,硕士研究生,研究方向为开关磁阻电机无位置传感器技术。
张 磊

