低压微电网概率潮流计算

黄春燕，刘皓明，钱程晨

（河海大学 能源与电气学院，南京 210098）

微电网是指由分布式电源、储能装置、能量转换装置、相关负荷和监控保护装置汇集而成的小型发配电系统，按结构可分为城市片区微电网、企业微电网和农村微电网3类[1]。城市片区微电网接入10 kV中压配电网，其微电源以燃料电池、微型燃气轮机和光伏为主；企业微电网接入10 kV及以上配电网，其微电源以传统电源为主；农村微电网由于容量较低，主要接入380 V低压配电网，被称为低压微电网，其微电源以风电和光伏为主，负荷既有三相又有单相，网络具有不对称和非全相运行的特点。

风电和光伏等微电源出力的间歇性和随机性会影响低压微电网的稳态运行，因此，通过潮流计算[2]来评估其稳态运行性能时需要计及风电和光伏出力的不确定性。低压微电网的显著特点是多种微电源同时出力，系统结构不对称性强，存在非全相运行情况，各相负荷不均衡。在一天内，光伏和风电的运行受天气影响，负荷的大小受用户行为影响，因此，需要借助概率潮流的概念来分析低压微电网的三相潮流分布[3]。概率潮流能反映微电网中各种随机因素对系统运行的影响，包括节点负荷值、电源出力等变量变化的不确定情况。只要获取了状态电压和支路潮流的概率密度函数和分布函数，便可对微电网的稳态运行特性进行评估。

适用于电力网络分析的概率潮流模型和算法被广泛研究[4—6]。对于分布式电源出力随机的特性，文献[7]研究了风速相关性对概率潮流计算结果的影响，并对其相关影响因素进行了分析，重点研究了风速相关性对节点电压概率密度分布、满足一定电压质量要求的最大允许风电装机容量和最小无功补偿量这3方面的影响。文献[8]考虑了配电系统负荷和风电场出力的不确定以及网络的三相不对称性，提出了基于蒙特卡罗模拟和三相潮流方程的概率潮流计算方法，分析了各相电压和不平衡因子的概率分布。文献[9]将概率潮流应用到地区电网研究中，根据风能、太阳能和电力负荷变化的规律性与随机波动特性，定义动态随机变量，并提出通过确定的变化规律与随机变量叠加来建立其概率模型。

鉴于光伏、风电出力和负荷在一天内波动较大，评估低压微电网稳态运行的安全性时需要综合考虑24 h潮流。本文基于日前预测建立了光伏、风电和负荷等随机变量的时间序列概率模型，采用不动点迭代法进行微电网三相潮流计算，给出基于蒙特卡罗模拟思想的微电网概率潮流计算方法。

1 元件的三相模型

低压微电网不仅包括一般而言的三相四线支路，还包括三相三线、两相三线、两相两线和单相两线等支路。本文定义网络的电压和电流均以相为单位，N相元件的支路导纳矩阵为N×N维。

1.1 微电源和负荷的三相随机模型

低压微电网的微电源一般以风电和光伏为主，其出力可以通过三相逆变器转换成380 V交流电或通过单相逆变器转换成220 V交流电。低压微电网的负荷也主要分为单相和三相2类。负荷、光伏和风电的典型功率曲线如图1所示。

本文将负荷、光伏和风电节点均看成是时变且三相平衡的PQ节点[9]。众多的独立随机因素影响着PQ值，由中心极限定理，可将任一时刻的PQ值看作是具有正态分布的随机变量[10]。因此，可结合预测数据和历史数据建立三者的时间序列概率模型，步骤如下：

（1）预测未来24 h内任一时刻的功率

基于数值气象预报获取未来24 h各时刻的气象数据，包括：风速和风向；太阳辐照强度、辐照时间；气温、最高气温和平均气温，然后选择合适的预测方法，获得未来24 h风电、光伏和负荷的功率序列Pit（i=1,2,3;t=1,…,T;T=24 h）。[11—12]

（2）概率分布特性参数的获取

假设时刻t的功率满足正态分布，即

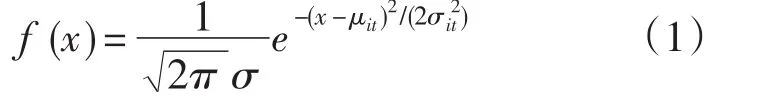
式中：μit和σit分别为元件i在时刻t的平均功率和功率标准差。

为任一预测时刻选择M个相似的历史时刻，用这些时刻的真实功率值辅助形成各随机变量的概率模型，能综合预测情况和真实情况，抑制预测方法带来的误差。将任一预测时刻对应的M个历史值表示为序列Pimt(i=1,2,3;m=1,2…,M;t=1,2…T)。

由日前功率预测值Pit和历史真实功率序列Pimt计算平均值和标准差

图1 负荷、光伏和风电的典型日功率曲线

1.2 线路的三相模型

低压微电网线路包含架空线路和地下电缆2类，线路的对地充电电容用集中参数表示，可等值为线路两端节点并联电容支路。将线路的并联支路作为首末节点的接地支路考虑后，三相线路在潮流计算时可统一使用图2所示的三相模型。

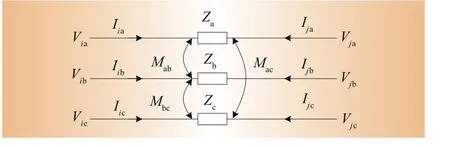
图2 线路L模型示意图

线路阻抗 ZZL矩阵可表示为

式中：Za、Zb、Zc分别为a相、b相和c相的自阻抗，Mab、Mac和Mbc分别为对应的相间互阻抗。

电压和电流的关系可表示为

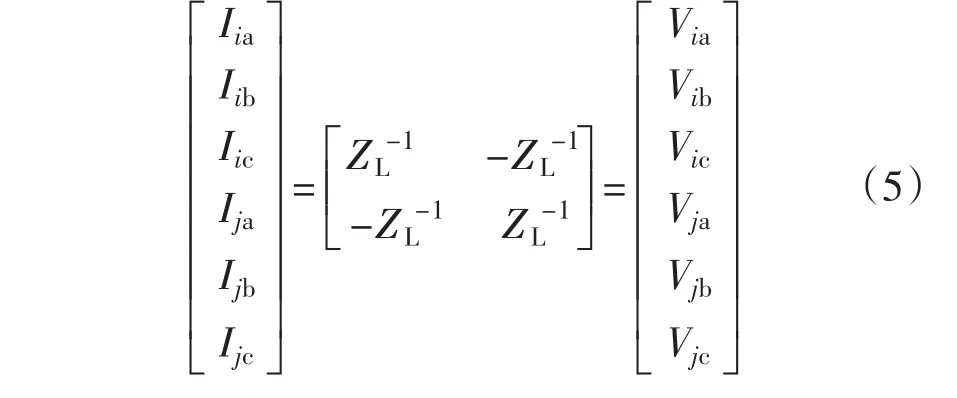
1.3 变压器的三相模型

低压微电网中的变压器通常为单相变压器，若存在三相变压器，可近似认为结构上三相对称，通过单相模型类推。考虑单相变压器支路k在节点i端接有理想变压器，变比为（用复数表示可能包含移相效果），如图3。

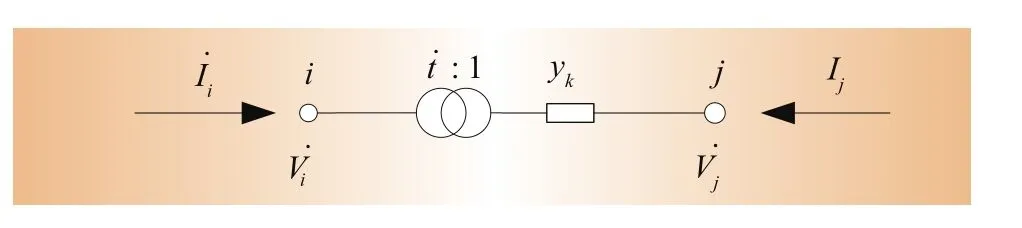
图3 变压器支路

变压器支路的节点方程可表示为

1.4 其他元件的三相模型

低压微电网中除风电和光伏外还可能存在少量的分布式电源，例如：燃料电池或者微型燃气轮机等，由于其容量小，出力稳定可控，可假设为出力恒定的PQ节点。

此外，常闭开关可等效为阻抗很小的线路，电压调节器可等效为变比接近1的变压器，移相器可等效为变比为1但相位非0的变压器，而其他串联元件均可参照线路元件建立阻抗模型，并联元件均可等效为所在节点的接地导纳支路。

2 概率潮流计算方法

OpenDSS是美国EPRI（电力研究协会）研发的配电网仿真软件，该软件计算含多种分布式电源且存在三相不对称的配电网潮流时采用了不动点迭代法和牛顿法2种计算方法。前者计算量小，适合大多数配电网络结构，后者计算较前者复杂但鲁棒性强。本文在此基础上结合微电网特性提出了改进的基于不动点迭代的三相潮流算法。

2.1 基于不动点迭代的三相潮流计算

设微电网与大电网的PCC点为平衡节点，其三相电压矢量给定为s，其余节点均为PQ节点，注入视在功率为Sn（n=1,…,N,N为微电网内除PCC点外的三相节点总数）。需要计算平衡节点注入视在功率Ss和其余节点的三相电压矢量为n。

由各支路的原始阻抗矩阵 ZZ和节—支关联矩阵A A形成系统的三相节点导纳矩阵 YY[[13]， YY的对角线元素中除了包含支路自导纳 YYL外，还包括节点对地导纳，如：线路对地充电电容、并联电容器等。将根节点的abc三相排在三相节点导纳矩阵 YY的最后三位，令根节点对应的方阵为Yss，其余节点对应的方阵为Yn，

基于不动点迭代法的三相潮流计算的主要步骤如下：

（5）根据式（5）、式（6）计算各类支路首末两端的三相电流，从而得到支路首末两端的三相功率。

2.2 基于蒙特卡罗模拟的概率潮流计算方法

为了模拟微电源和负荷的三相随机模型，采用蒙特卡罗概率方法产生大量的随机数据，调用上节所提的确定性潮流计算方法。主要步骤如下：

（1）建立微电网中线路等元件的三相模型。

（2）基于数值气象预报和合适的预测方法，得到风力、光伏和负荷的次日功率预测数据。

（3）建立风力、光伏、负荷的时间序列概率模型，确定各时刻各元件所满足的正态分布的均值和标准差参数。

（4）基于时间序列概率模型，生成蒙特卡罗模拟过程所需的足够数量的随机数。

（5）基于改进的三相潮流前推回代法进行蒙特卡罗模拟，计算足够数量的各时刻系统潮流[14]。

（6）通过统计分析，获得潮流解的概率分布特性，计算电压不平衡度、系统电压综合不平衡度等指标。

3 算例分析

本文采用改动的IEEE 123节点测试系统[15]进行仿真，系统如图4所示，系统中除三相线路外还包含3条两相线路和55条单相线路。节点150、9、160、25接了400 V电压调节器，节点149、152、60、18接了常闭开关，节点83、88、90、92接了电容器。

图4 IEEE123节点测试算例图

为了模拟微电网中的微电源，在原有算例的基础上接入了分布式电源，如表1所示。

采用BP型人工神经网络方法预测日前功率Pit[16]序列，为每一个预测时刻选择M个相似时刻的历史数据来表示日前功率的近似功率Pimt，利用式（2）和式（3）分别计算功率的期望值序列和标准差序列。根据已经得到的光伏、风电和负荷的时间序列概率模型获取蒙特卡罗模拟所需的随机数。

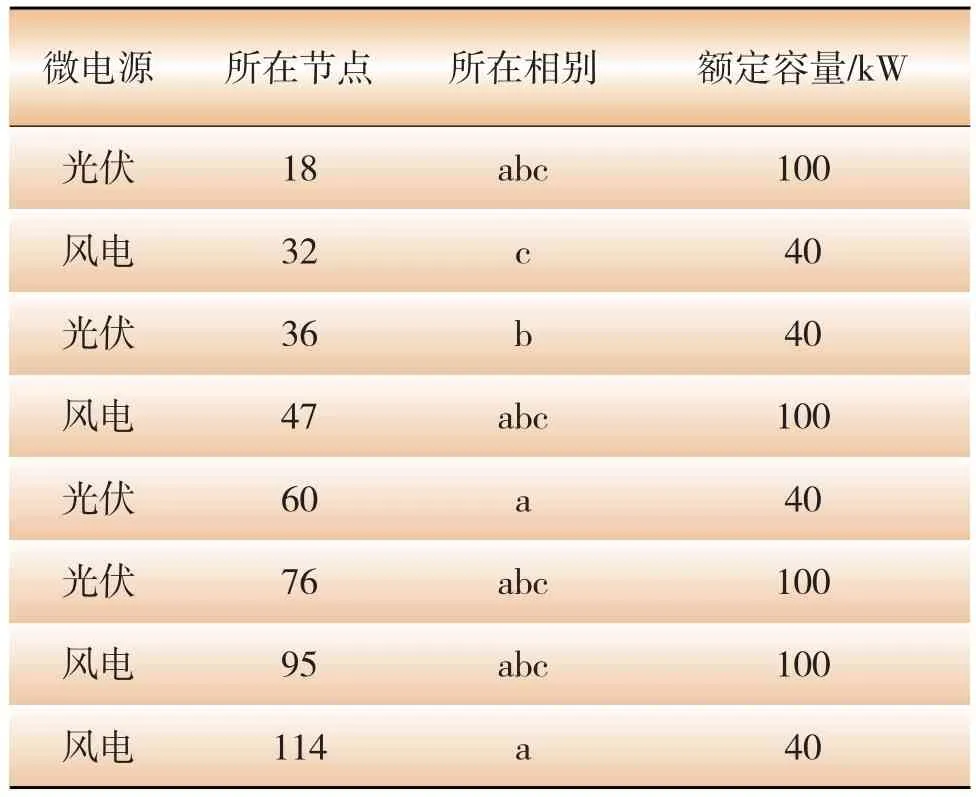
表1 新增的微电源分布情况

建立线路、电压调节器、开关、电容器的三相模型，应用基于不动点迭代法的改进三相潮流计算方法计算潮流，模拟次数为1 000次。通过对计算结果进行统计分析，得到各个时刻的潮流概率分布，即时间序列概率潮流。图5是节点60的三相在次日12：00时电压幅值的概率密度函数图。

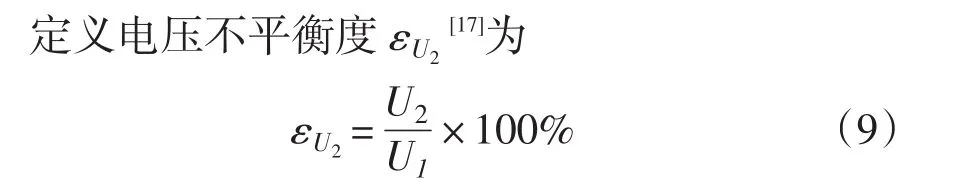
式中：U1和U2分别表示任一节点三相电压的正序分量和负序分量。以节点60为例，先计算一天各个时刻每次模拟的3个相电压的大小，计算出正序分量和负序分量，然后获得εU2值，最后可取所有值的平均得到电压不平衡度期望值为0.78%。

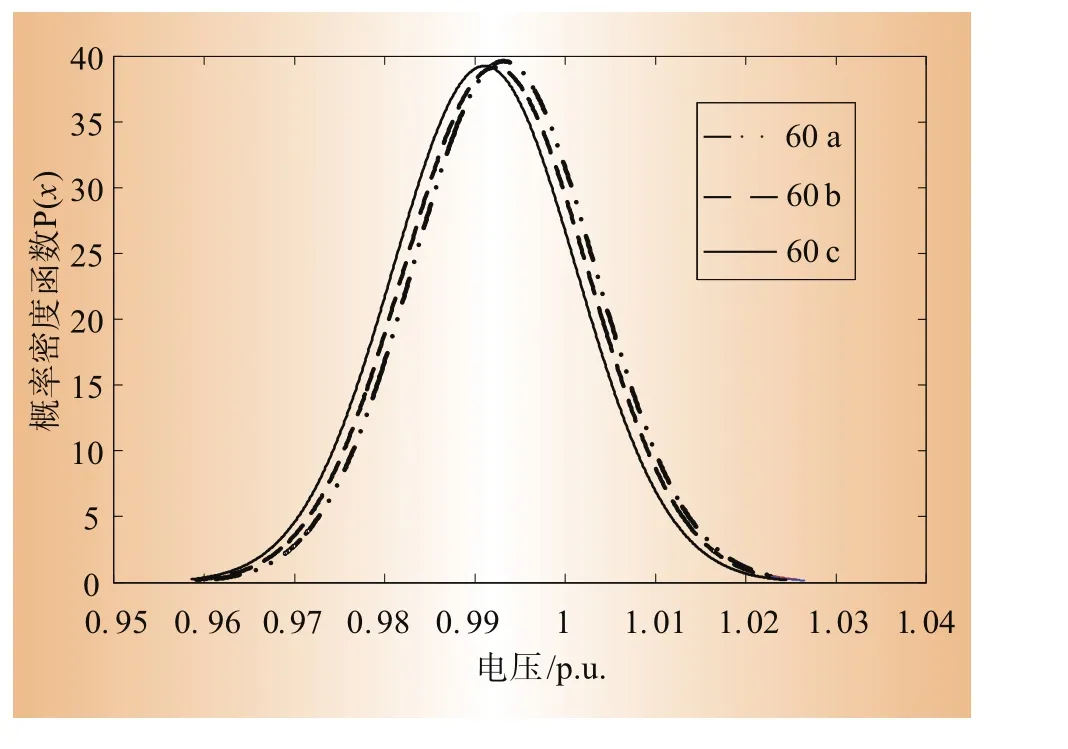
图5 次日12：00节点60的三相电压概率密度图

图6是PCC节点（节点150）在次日12：00时的有功功率概率密度函数图，模拟了投入所有分布式电源和不投入分布式电源2种情况。由图6可知：未投入分布式电源时需要大系统注入有功功率期望值为515.89 kW，投入分布式电源时该值降为12.87 kW，投入分布式电源有效地降低了微网对外网电能的需求，并且由于分布式电源出力的随机性，含有分布式电源后PCC点功率标准差从35.34 kW升为68.37 kW，系统有功功率不确定性增强。

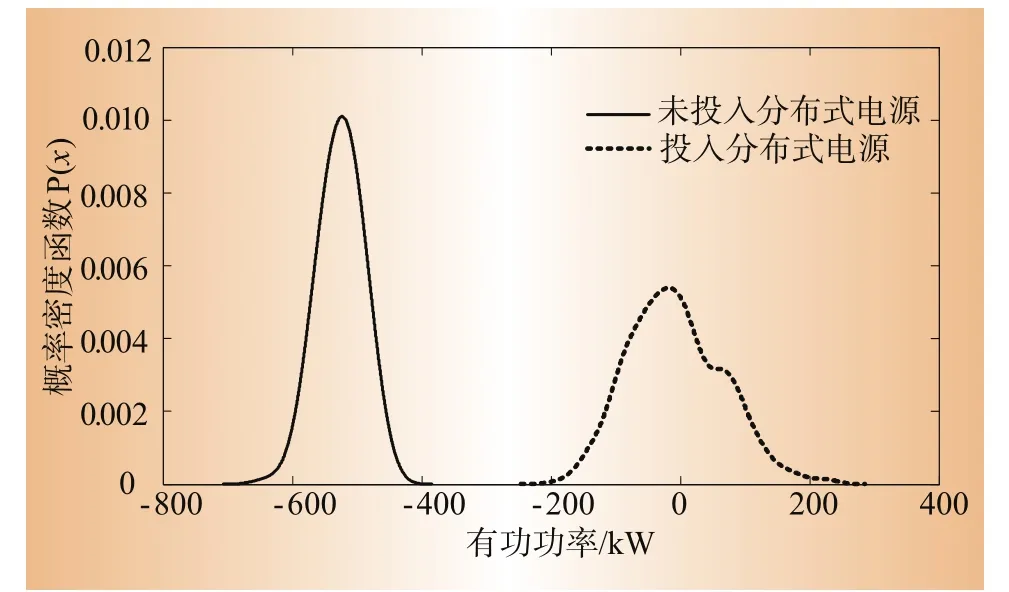
图6 节点150有功功率的概率密度函数图

节点38与节点36位于同一条馈线，且位于馈线的下游。图7显示了节点36的b相投入光伏前后对节点38的b相电压水平的影响，可以看出，节点36的b相光伏功率的注入显著提高了馈线的电压水平。

图7 节点36投入光伏前后节点38电压概率密度函数图

4 结束语

针对低压微电网具有微电源出力随机性强、三相不平衡、非全相运行等特点，提出了一种基于日前预测的微电网概率潮流计算方法。风电和光伏的时间序列概率模型同时计及了一天的普遍波动和特定时刻的随机波动，优于常规的概率潮流计算。基于不动点迭代的分相潮流计算方法解决了常规配电网潮流计算无法完善处理的多电源、三相不平衡和非全相等问题。经典蒙特卡罗法得到的微电网概率潮流分布的概率特性为微电网运行状态评估提供了依据。

[1] 时珊珊,鲁宗相,周双喜,等.中国微电网的特点和发展方向[J].中国电力,2009,42(7)：21-24.

[2] 刘杨华,吴政球.孤岛运行的微电网潮流计算方法研究[J].电力系统保护与控制,2010,38(23)：16-20.

[3] 董雷,程卫东,杨以涵.含风电场的电力系统概率潮流计算[J].电网技术,2009,33(16)：87-91.

[4] 胡金磊,张尧,李聪.交直流电力系统概率潮流计算[J].电网技术,2008,32(18)：36-40.

[5] 刘浩,侯博渊.保留非线性的快速P-Q分解随机潮流分析[J].电力系统及其自动化学报,1996,8(1)：8-17.

[6] 丁明,李生虎,黄凯.基于蒙特卡罗模拟的概率潮流计算[J].电网技术,2001,25(11)：10-14.

[7] 范荣奇,陈金富,段献忠,等.风速相关性对概率潮流计算的影响分析[J].电力系统自动化,2011,35(4)：18-22.

[8] CaramiaP,CarpinelliG,PaganoM,etal.Probabilisticthree-phase load flow for unbalanced electrical distribution systems with wind farms[J].IETRenewablePowerGeneration,2007,1(2)：115-122.

[9] 余昆,曹一家,陈星莺,等.含分布式电源的地区电网动态概率潮流计算[J].中国电机工程学报,2011,31(1)：20-25.

[10] Wang J H，Shahidehpour M，Li Z Y.Security-constrained unit commitment with volatile wind power generation[J].IEEE TransactionsonPowerSystems,2008,23(3)：1 319-1 327．

[11] 李建红,陈国平,葛鹏江,等.基于相似日理论的光伏发电系统输出功率预测[J].华东电力,2012,40(1)：153-157.

[12] 吴军基,倪黔东,孟绍良,等.基于人工神经网络的日负荷预测方法的研究[J].继电器,1999,27(3)：27-28.

[13] 张伯明,陈寿孙，严正.高等电力网络分析[M].第二版.北京：清华大学出版社,2007.

[14] 段玉兵,龚宇雷,谭兴国,等.基于蒙特卡罗模拟的微电网随机潮流计算方法[J].电工技术学报,2011,26(1)：274-278.

[15] Jason Fuller.Distribution Test Feeders[EB/OL].http：//www.ewh.ieee.org/soc/pes/dsacom/testfeeders/index.html.

[16] 牛晨光,刘丛.基于相空间重构的神经网络短期风电预测模型[J].中国电力,2011,44(11)：73-77.

[17] 全国电压电流等级和频率标准化技术委员会.GB/T 15543—2008,电能质量——三相电压不平衡[S].北京：中国标准出版社.