贝叶斯网络在车辆状态远程故障诊断系统中的应用

郭文强， 付 菊， 张玉杰， 侯勇严

(陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

0 引言

汽车产业已成为我国国民经济的支柱性产业之一.及时、准确地掌握车辆的运行状态，有利于节能环保和交通通畅，更为驾乘人员的人身、财产安全和维修企业高效、合理安排检修工作等提供了保障依据[1].而借助现代的通信手段建立车辆状态远程监测与故障诊断系统，可以对行驶车辆的实时状态进行监测及故障分析、预警，从而有效地建立起车辆运行状态的信息共享与交流平台.

在车辆故障诊断方面，传统的基于规则的专家系统的分析过程中，主要利用推理机将用户输入的信息与知识库中各个规则的条件进行匹配，并把被匹配规则的最终结论呈现给用户.但由于其知识和规则是提前就存储好的数据，而推理中往往存在一定的模糊性，所以专家系统分析速度快但精确度不高.

人工智能作为一门新兴的智能技术为车辆故障检测和诊断技术的发展提供了强有力的技术手段和实现的可能性.文献[2]验证了将粗糙集与反向传播(Back-propagation)神经网络(简称BP)进行融合对车辆常见故障进行诊断的可行性和有效性.文献[3]探讨了将径向基函数(Radial Basis Function)神经网络(简称RBF)应用于车辆远程的故障诊断的方法.

随着新技术、新结构和新工艺的大量涌现，车辆故障诊断日趋复杂，导致车辆的诊断对象和原因间的因果关系不一定是确定的一一对应的映射关系，而是表现为随机性和不确定性[4,5].传统故障诊断方法逐渐显示出诊断效率和准确性低下、建立诊断系统可维护性差等方面的不足.贝叶斯网络(Bayesian network，简称BN)由于其有机结合了概率论和图论的理论基础，成为目前不确定性问题表示和推理的有效模型，可以解决复杂系统中各种不确定性因素下的故障诊断与决策问题[6].

本文将贝叶斯网络运用于车辆状态远程故障诊断系统，通过贝叶斯网络对复杂系统的建模和推理，完成车辆的故障分析与诊断，增强了诊断系统处理不完备、含噪数据的能力.

1 车辆状态远程故障诊断系统的结构及组成

车辆状态远程故障诊断是一种基于知识处理的测控与诊断方法.它以计算机为工具，模仿人类专家对复杂系统进行工况监控与故障诊断，既能充分地发挥专家的知识和经验，进行快速推理，又可以方便地推广应用至各种不同的监控与诊断对象.本文设计的车辆状态远程监测与故障诊断系统的结构示意图如图1所示.

图1 车辆状态远程监测与 故障诊断系统架构

该系统主要由车载子系统、通信网络子系统、车辆状态监测及故障分析子系统等三部分组成.其主要工作原理如下：车载子系统利用车辆上安装的运行状态传感器组将车辆状态参数采集并完成预处理，然后通过移动通信网络接口模块，将车辆的状态信息通过GPRS(General Packet Radio Service，通用报文分组业务)模块发送给车辆维修企业或车辆管理中心的状态监测及故障分析子系统，经过中心服务器预处理和分析归纳(本系统采用的是基于贝叶斯网络的故障诊断)后，再把分析结果发送至车辆管理中心以及远程车辆上的综合电路板，把结果显示给或者提示给驾驶员，便于尽早预防隐患及排除故障.

其中：车载子系统由运行状态传感器组、状态参数采集和预处理模块以及移动通信网络接口模块组成，利用GPRS系统(传输速度可达100 K)能使车辆宽频网络无线连接得到实现，利用移动通信网络把车辆状态信息传送到设置于车辆维修企业或车辆管理中心的服务器中.

通信网络子系统，本设计采用了GPRS无线通信技术的方案.GPRS是基于GSM架构的一种端到端的报文交换业务.采用GPRS的主要原因是随着移动手机业务的不断普及，相应的GPRS服务覆盖区域也日益增大，且GPRS数据传送业务资费低于专网的维护费用，安装、维护便捷.该子系统作用是通过GPRS网络与基站进行数据链接，再由基站把数据汇集到Internet互联网中，使数据的传输范围更为广泛.

车辆状态监测及故障分析子系统，是由一个与互联网相连的小型局域网组成，通过管理平台使车辆信息数据库服务器、数据分析计算机、快速以太交换机等设备的协同工作，来完成车辆的状态监测与故障分析.

2 故障诊断贝叶斯网络及其工作原理

贝叶斯网络，又称概率因果网络、信任网络等，是一种有向无环图.本车辆故障诊断系统的故障诊断采用贝叶斯网络模型，充分利用贝叶斯网络处理不确定信息的优势，判断出故障节点.模型的建立和推理是故障诊断系统的核心.其工作过程为：首先由诊断对象的实际数据结合知识库中的专家知识建立贝叶斯网络故障诊断模型，并将实时数据作为相应观测值(证据)利用联合树等推理算法完成推理，计算出节点集的后验概率，得到该结果发生的原因以及事件发生的概率，为车辆的运行、维护与维修提供决策参考.

2.1 数据预处理

故障诊断问题实际上是一个模式识别的问题.以车辆中常见电喷发动机故障为例，发动机本身是一个复杂的动态系统，用以表达其运行状态的参数很多.文献[2]根据几种常见发动机，建立了车辆故障信息表，其中采用的模拟量有节气门开度(C1)、气流量(C2)、燃油压力(C3)、冷却水温(C4)和扭矩(C5)，数字量有转速(C6)和喷油脉宽(C7).故障类别(E)分为5类，即正常、水温高、空气流量计损坏、喷油器故障和点火故障，分别采用数字1至5表示.

为了加快故障诊断的推理速度，对连续属性进行离散化，即将数值按属性值划分成若干个子区间，并以此区间代替原有的真实值，从而使诊断对象特征得以凝练.对连续数值进行离散化的方法有很多，为方便对比，本文仍采用文献[2]的阈值法和量化区间将连续属性值进行量化，进行离散化之后的信息表如表1所示.

表1 离散化后电喷发动机信息表

2.2 故障诊断推理贝叶斯网络

2.2.1 贝叶斯网络

定义对于一个变量集U={x1,…,xn}，其对应的贝叶斯网络是一个二元组，即B={G,Θ}[7].其中，G={V,E}为一个有向无环图(简称DAG)，节点V与变量集U一一映射，E为连接各节点的有向边.Θ={Θi,i=1,…,n}是一组条件概率分布，它与在G中给定了双亲节点xi的条件概率一一映射.一个结构为G的贝叶斯网络关于U的联合概率分布可由下式表示：

(1)

其中πxi是G中节点xi的双亲节点.

2.2.2 BN故障诊断模型构造

由贝叶斯网络定义可知，其模型由网络拓扑结构和局部概率分布集合两部分组成，因此贝叶斯网构造(又称学习)可以分为结构确定和参数确定[8].根据样本数据，并利用已有的贝叶斯网络结构学习和参数学习算法构建、修正故障诊断所需推理机模型，用以满足诊断系统对不确定性问题建模和推理等要求.

而对于熟悉的研究对象，可以结合先验知识，进行BN模型构造，减少建模时间.其中模型结构常可根据领域专家经验构建.贝叶斯网络的参数学习常分为完备数据和不完备数据两种情况.对于完备数据的网络参数学习可采用最大似然估计(Maximum Likelihood Estimate) 算法获取；而对于不完备数据的网络参数学习可采用期望最大化(Expectation-maximization，简称EM) 算法获得，从而确定结构中每个节点的条件概率.

EM算法是一种计算最大似然函数的通用算法，其主要思想是在开始设定一个初始估计θ0，然后不断地修正它.从当前的估计θt，到下一个估计θt+1需要两个步骤：期望计算(E-Step)和最大化(M-Step).

设πi为结构S中变量xi的父节点集，则p(xi=j|πi=k)表示给定πi为第k种可能取值时，节点xi为第j种取值的概率，记为θijk.

(2)

其中：mijk是p(xi=j|πi=k)的个数.

由于样本数据可能存在缺失，导致部分充分统计因子Nijk和Nik未知.EM算法的E-Step利用当前的贝叶斯网结构和参数计算样本中缺省数据的期望充分统计量ESS：E(Nijk)和E(Nik)，然后利用E(Nijk)和E(Nik)重新估计当前网络的参数.EM算法描述如下.

EM算法：首先初始化网络的参数θ0，重复E-Step和M-Step直到收敛.

E-Step：利用t步的贝叶斯网参数θt选择合适的网络推理机计算E(Nijk|θt)和E(Nik|θt).

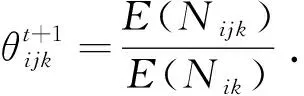
2.2.3 基于贝叶斯网络的故障诊断推理

联接树算法(Junction tree，简称JT)是目前贝叶斯网络精确推理中计算速度最快、应用最广的推理算法[7].本文的贝叶斯网络的推理即选用了联接树算法.首先，将有向无环图G转变为联合树T=(C,S) (其中C为簇集，S为分隔集).随后在T上进行信度传递与吸收，通过在T上进行收集证据信度 (Collect-Belief)与发散证据信度 (Distribute-Belief)两个阶段相反方向的信度传递，即在T上随机选择一个簇作为根节点，分别通过Collect-Belief算法与Distribute-Belief算法实现信度的势在T上全局传播，利用信度吸收算法使T上信度的势满足一致性.

故障概率的局部计算包括边缘化运算和条件概率的计算.对于故障原因节点V=vi，识别一个包括节点vi的一个簇或者分隔X，边缘化其信度势φX可计算得到P(V)，即:

(3)

对于边缘化运算，利用公式(3)在T上找出包括故障征兆与故障原因节点的簇或分隔，计算其故障概率分布.

条件概率的计算，即在故障征兆节点ev出现时计算故障原因节点V的概率P(V|ev)，计算公式如下:

(4)

对复杂系统进行故障诊断，实际上就是根据一定的故障征兆，推理得到某个或某些故障原因，因此故障诊断本质上是模式识别问题.基于贝叶斯网络的车辆故障诊断基本原理为：在模型确定后，通过数据采集，以车辆状态征兆节点(属性)为起始点，根据故障知识库和推理机，依据式(4)找出状态节点最大概率的节点，即由网络节点之间的依赖因果关系和概率分布推理得出各种故障原因发生的概率，进行故障原因判断，从而得到诊断结论.

3 实验评估

为了验证以上基于贝叶斯网络进行故障诊断方法的正确性和有效性，进行了以下实验.实验运行的硬件环境为2G内存、2.5GHz Pentium(R)Dual-core CPU的计算机，软件采用Matlab7.1.其中，贝叶斯网络工具包采用了Kevin Murphy开发的开源贝叶斯网络工具包BNT[8].

3.1 建模实验

由贝叶斯网络定义可知，其模型由网络拓扑结构和局部概率分布集合两部分组成，因此贝叶斯网建模可以分为结构确定和参数确定.

车辆故障诊断贝叶斯网络依据专家经验获取的结构模型如图2所示.参数确定采用了表3的车辆样本数据，利用EM算法，得到了网络节点的1张先验概率分布表和7张条件概率分布表.其中P(F)={ 正常，水温高，空气流量计损坏，喷油器故障，点火故障}，其先验概率分布为[0.3 0.2 0.1 0.2 0.2 0.2]，P(C1|F) 和P(C7|F)的条件概率分布表分别如表2和表3所示，类似可得到所有节点的条件概率分布表.

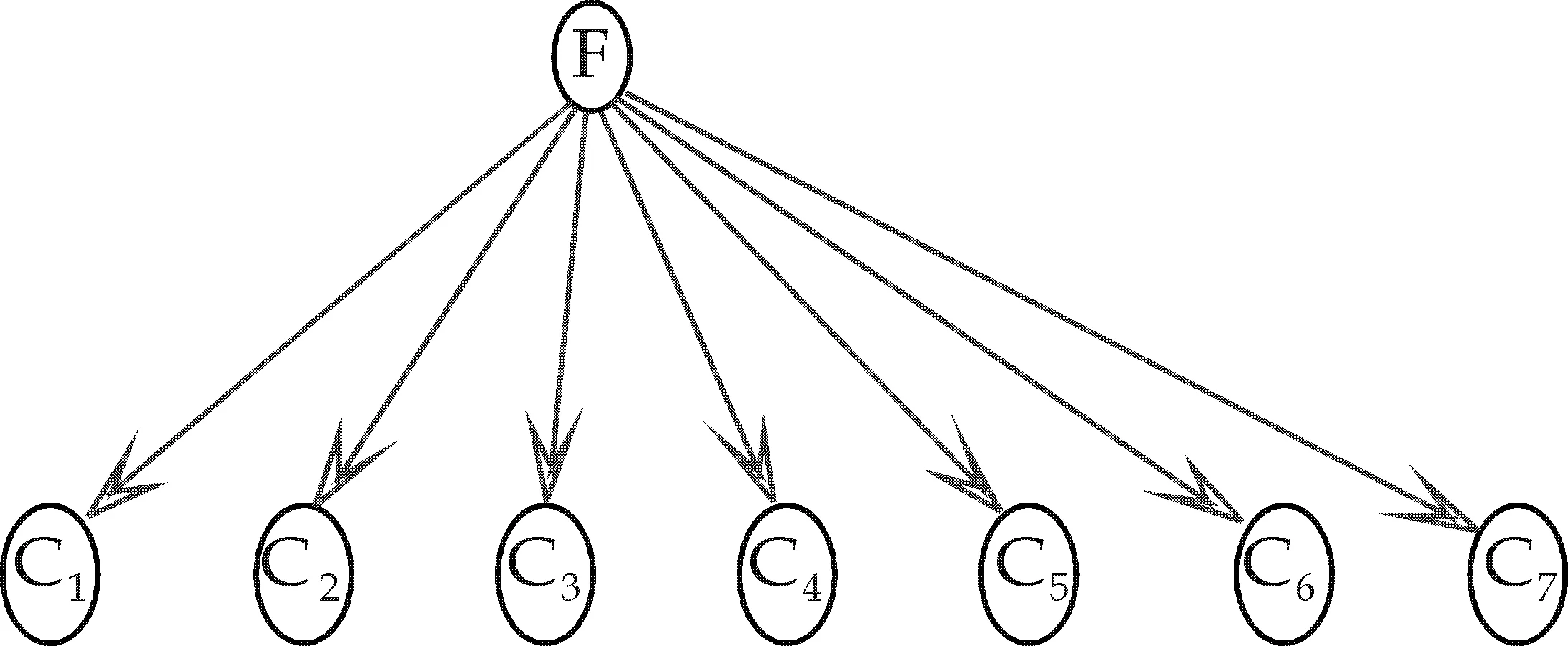
图2 车辆故障诊断贝叶斯网络结构模型

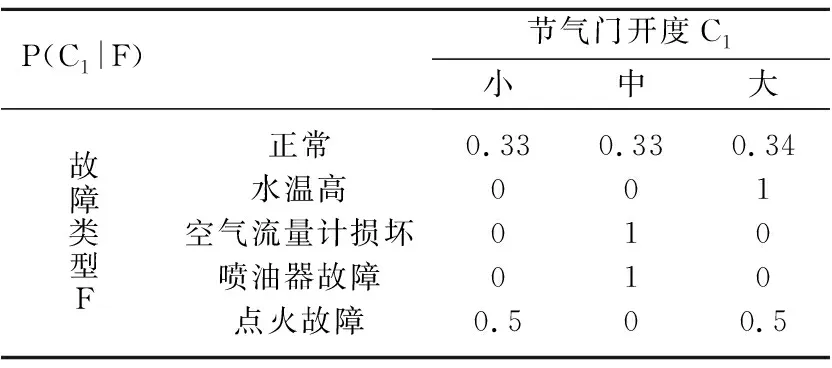
P(C1|F)节气门开度C1小中大故障类型F正常水温高空气流量计损坏喷油器故障点火故障0.330000.50.3301100.341000.5

表3 P(C7|F)条件概率分布

实验中，相邻两次迭代误差取0.1‰.采用BN模型，其参数学习过程利用EM法重复进行了20次，计算出平均耗时列于表4.为方便对比，同等迭代误差下，采用BP方法及RBF方法进行模型的参数学习，学习平均耗时见表4.

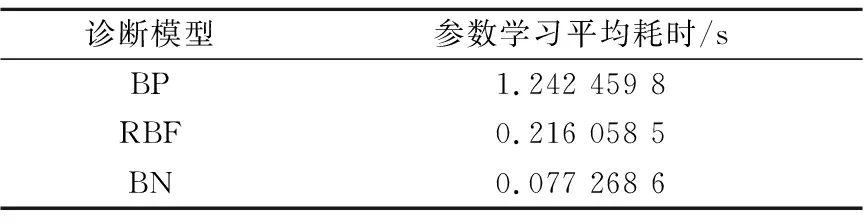
表4 不同故障诊断模型参数学习20次平均耗时

对比可知：在本案例同样条件下，采用贝叶斯网络方法所需模型参数学习平均耗时最短，约为0.077 268 6 s.说明本文所采用方法，在建模方面具有快捷的优点.

3.2 完备证据下推理诊断实验

基于本文提出的BN诊断模型，利用联结树算法进行故障诊断的结果如图3所示.利用RBF模型和粗糙集-BP模型进行故障诊断的结果和真实故障诊断类别亦列在图3中.图4是三种诊断方法针对10组样本分别进行推理耗时及平均耗时情况.由图4中可以看出，诊断推理中采用BN法推理速度最快.

实验结果表明，在以上三种诊断方法中，采用贝叶斯网络法进行故障诊断分类效果最为理想.

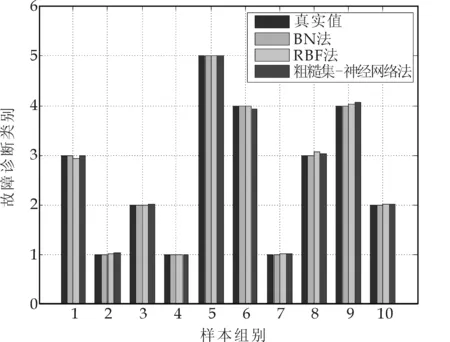
图3 不同诊断方法进行车辆 故障诊断结果

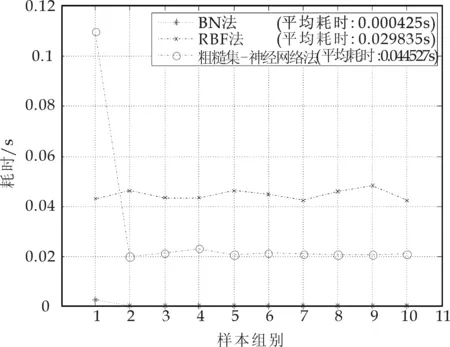
图4 不同诊断方法进行故障 诊断推理耗时对比

3.3 不完备证据下推理诊断实验

相较其他故障诊断方法，贝叶斯网络方法除了具有坚实的理论基础外，还体现在它处理不确定性问题能力方面具有较强的优势.在实际系统中对数据进行处理时，往往会出现数据的缺失及噪声影响问题.贝叶斯网络由于具有条件独立性假设，从而有效地解决了样本数据间的不确定性问题，达到对样本数据充分利用的效果.

表5中列出了表3中第10组样本组序列出现异常的情况.现假设证据出现了不完备即数据缺失，本用例中假设C5证据由于某种原因出现了缺失，此时若采用传统的神经网络建模方法，除非利用数据修补等剧增推理运算复杂度的技术，否则，诊断推理将不可进行.为了让问题更复杂化，本用例中C4证据还由于噪声原因使证据值较真实值出现了偏差，实际值应为“3”，而相应的观测值为“2”.

利用本文的贝叶斯网络诊断方法，在数据完备和出现不完备、含噪时进行诊断结果列于表5.对比可知，诊断推理与真实情况一致.实验结果表明，本诊断方法具有较强的鲁棒性.

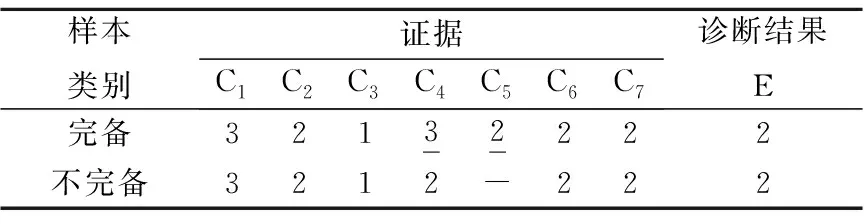
表5 数据出现异常状况下BN法故障诊断推理

4 结束语

本文将贝叶斯网络应用到车辆状态远程故障诊断系统中，利用基于贝叶斯网络模型的故障诊断方法，可以方便地利用机器学习等知识发现技术进行故障诊断推理机的建模，并有效地融合先验知识信息，使诊断模型更好地处理实际系统中的不确定信息，结合贝叶斯网络的推理算法，可得到有效的故障诊断结果.

实验结果表明，对于复杂系统，贝叶斯网络方法在诊断速度、诊断结果准确性等方面优于传统的基于BP算法或RBF算法的诊断方法，并且有一定处理数据缺失和含有噪声数据的能力，提高了故障诊断系统的鲁棒性.

[1] 岳现杰.基于无线网络的车辆健康状态管理系统研究[J].计算机测量与控制，2012，20(2):297-299.

[2] 傅晓林，王兴家，蔡辰光.粗糙集与神经网络在发动机故障诊断中的融合应用[J].重庆交通学院学报，2006，25(6):130-134.

[3] 姜 鑫，傅晓林，杨志刚.RBF神经网络分析方法在车辆状态远程监测系统中的应用[J].汽车实用技术，2011，9(3)：23-26.

[4] 郭文强，张玉杰，侯勇严.基于贝叶斯网络模型构造的汽车故障诊断研究[J].计算机仿真，2011，28(11):315-317，353.

[5] 干能强，杜宏明，谢 晖.基于RBF网络的滚动轴承故障诊断[J].陕西科技大学学报,2008,26(2):90-92,96.

[6] 杨昌昊，胡小建，竺长安.从故障树到故障贝叶斯网映射的故障诊断方法[J].仪器仪表学报，2009，30(7)：1 481-1 486.

[7] Judea Pearl.Causality: Models，reasoning and infer- ence (2nd edition)[M].Cambridge: Cambridge University Press, 2009.

[8] Kevin Murphy.Dynamic Bayesian Networks: Represent-ation，Inference and Learning[D].UC Berkeley: Computer Science Division，2002.