供应商风险等级评估的二元语义模型与方法
李登峰 杨 洁
(福州大学管理学院,福建福州 350108)
一、引言
进人21世纪以来,随着经济全球化程度的加深,供应链及其管理在运作中发挥着越来越重要的作用。随着供应链中断事件的频繁发生及其脆弱性问题的提出,供应链风险(Supply Chain Risk,SCR)管理逐渐成为供应链研究的一个重要领域。供应商作为供应链的源头,供应商风险经“牛鞭效应”进行扩大,从而可能导致供应链无法正常运转,甚至导致供应链的破裂和失败。供应商风险的识别与评估是有效进行供应商风险管理的重要阶段,是发现潜在风险、为供应商风险管理其他阶段工作提供依据的重要过程。因此,供应商风险的识别与评估在供应链风险管理中占有举足轻重的地位。
关于供应商问题的研究,目前主要从供应商选择与评估方面开展,且取得了一定的成果。[1][2][3]随着供应商成员数目的逐渐增加、企业间合作的逐渐深入,供应商结构日趋复杂,供应商的运作和管理上的风险因素不断增加。目前,专门针对供应商风险预测评估的研究还相对较少,其主要思路是通过对供应商潜在风险进行识别,建立风险指标体系,然后利用多属性综合评价进行评估。陈丽虹等认为供应商风险管理中有五大风险指标,即财务生存能力风险、资金周转风险、产品翻新风险、供应商权力风险、地理位置政治形势风险。[4]赵爱武等用德尔菲法通过问卷获取供应商风险关键指标因素及指标因素间的关系,然后运用网络分析法进一步确定各指标因素的权重和排名,以此建立供应商风险评估指标体系。[5]丁斌等首先运用粗糙集理论对繁杂的供应商风险指标体系进行精简确定指标权重,并运用未确知测度模型对供应商风险进行评估,从而实现对各供应商风险的比较探讨。[6]陈新平基于紊乱环境(包括行业内部和外部),通过对内生风险和外生风险的分析,提出了一种供应商风险预测模型来识别和预测供应风险,并根据供应商的属性、绩效和供应链特点等进行评价及选择供应商。[7]此外,Jennifer等结合供应商风险因素及其汽车行业特点进行分析,提出了一种动态的风险分析方法,该方法结合风险评价和监控系统,分析及监控供应商的风险水平随时间推移的变化规律。[8]刘庆广与施国洪在系统地梳理供应商风险来源的基础上,建立了供应商风险指标体系,并将供应商风险分为竞争型风险、中断型风险、制度型风险和战略型风险四类,进一步利用风险频度-风险损失矩阵对四类风险进行分析。[9]
通过对文献分析可知,多数研究都把供应商风险的排序评估与供应商风险等级评估当作同一类问题来解决,即在获得供应商风险综合值后,根据设定的风险等级阈值,判断供应商风险综合值是否满足阈值条件来确定供应商的风险等级。然而,从等级评估的概念和方法论角度看,风险等级评估是不同于风险排序评估的。为此,本文将从供应商风险等级评估概念出发,建立供应商风险等级评估的一般性模型,并在数理层面上分析其合理性、有效性,旨在揭示供应商风险等级评估中出现一些“表面上看似科学,而实际上是不科学甚至是伪科学”的方法,从而提升供应商风险评估的质量和可信度。
二、供应商风险等级评估的综合级别判定
(一)隶属度原则评估法
设有n个供应商Tj(j=1,2,…,n)组成供应商集 T={T1,T2,…,Tn},m 个风险指标 fi(i=1,2,…,m)组成风险指标集 F={f1,f2,…,fm};用ek(k=1,2,…,h)表示第 k个风险等级,且规定e1>e2>… >eh,即第k个风险等级ek比第k+1个风险等级ek+1强,所有h个风险等级组成风险等级集 E={e1,e2,…,eh};供应商Tj关于 fi的风险等级ek的特征值为yijk=fik(Tj)。用矩阵形式可直观地表示为Yj=(yijk)m×h,称为供应商Tj的风险级别特征值矩阵。在Yj中,第i行表示供应商Tj关于风险指标fi的所有风险等级的特征值,而第k列表示供应商Tj关于风险等级ek的所有风险指标的特征值,记为 yj=(y1jk,y2jk,…,ymjk)T(k=1,2,…,h)。
供应商风险等级特征值 yijk(i=1,2,…,m;k=1,2,…,h)的类型通常是不一样的,需对其做类型一致化和无量纲化处理,即做规范化变换或映射 φ1:R →[0,1]使得
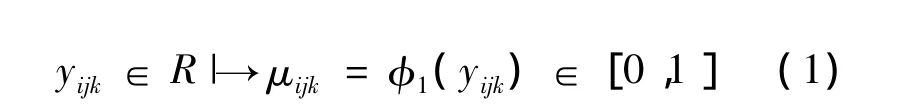
式中:φ1是风险指标级别特征值规范化方法。
利用式(1)可将 Yj规范化为μj=(μijk)m×h,称为供应商Tj的规范化风险指标级别特征值矩阵。类似地,用μjk=(μ1jk,μ2jk,…,μmjk)T表示Tj关于ek的所有风险指标的规范化特征值。但事实上,风险等级的划分是1个包含较大主观性的模糊概念。因此,μj可看作是F与E之间的1个模糊关系,从而μijk就是Tj关于fi对风险等级ek的隶属度,μjk则是Tj关于ek的所有风险指标的隶属度向量。
按照某种供应商风险等级评估方法或集结算子φ:[0,1]2m+h→[0,1]h,可得供应商Tj(j=1,2,…,n)对于所有风险等级ek(k=1,2,…,h)的综合隶属度向量为
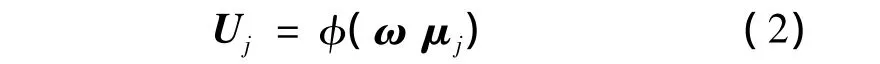
式中:ω =(ω1,ω2,…,ωm)T是风险指标权重向量,Uj= (uj1,uj2,…,ujh),φ(ω,μj)= (φ(ω,μj1),φ(ω,μj2),…,φ(ω,μjh)),ujk= φ(ω,μjk)这样,Uj=(uj1,uj2,…,ujh)可看作为隶属度向量。把 n个供应商的风险等级综合隶属度向量用矩阵形式可直观地表示为U=(ujk)n×h,称为供应商风险等级综合隶属度矩阵。

式(2)的一种比较简单的具体形式就是常用的线性加权综合评估模型[10]:
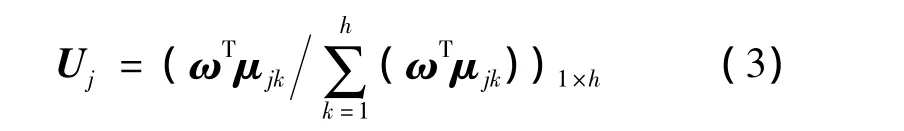
在现有关于等级评估文献中,通常利用最大隶属度原则评定风险等级[10],但最大隶属度原则仅仅考虑隶属度的相对大小,没有考虑各个风险等级的位置差异,这将导致结果出现诸多的不合理,如u1k=(0.3,0.25,0.45),根据最大隶属度原则,供应商T1的风险为3级,未考虑到属于第1级与第2级的风险隶属度之和为0.55,大于第3级的风险隶属度。因此,有必要提出能综合考虑风险隶属度相对大小和风险等级位置差异的风险等级评定原则。
(二)等级评估级别判定值
将风险等级ek(k=1,2,…,h)的级别变量定义为k,并把供应商Tj(j=1,2,…,n)的级别判定值定义为

尽管供应商Tj的级别判定值υj是介于1与h之间的实数,但多数情况下不是整数。一种自然、简单的方法是:若

则将Tj评定为k级风险即ek,其中[υj]表示不大于υj的最大整数。
三、供应商风险等级评估的二元语义方法与过程
现实中,可能会出现与直观判断不一致的级别判定情况,如表1所列的级别判定值。因此,有必要在评定的供应商风险等级的基础上,进一步区分相同风险等级的差异程度。

表1 供应商风险级别判定值
由表 1 和式(5)可得:[υ1]=1,[υ2]= [υ3]= [υ4]=2,[υ5]=3,从而可做出Tj(j=1,2,…,5)的风险等级评定结果为:T1面临1级风险,T2、T3和T4面临2级风险、T5面临3级风险。然而,这样的结论似乎与直观判断不一致。事实上,仔细分析发现,υ1=1.98与υ2=2.03都比较接近于2,且两者之间相差很小,把υ1与υ2相对应的T1和T2分别评定为1级风险、2级风险是不合理的。直观上,T1和T2应属于相同的风险等级即第2级。同样分析可以看到,υ2=2.03、υ3=2.34 和 υ4=2.98 都是小于3的数,但它们的差异是比较明显的:υ2=2.03与2非常接近,且其与2的差异程度比υ3=2.34 与2 的差异程度要小,比 υ4=2.98 与2的差异程度更小。此外,υ4=2.98已经比较接近于3。因此,把υ2、υ3和υ4相对应的T2、T3和T4都评定为面临2级风险是不合理的。直观上,T2和T3应属于2级风险供应商,而T4属于3级风险供应商。进一步地,T1、T2和T3都属于2级风险供应商,但它们的隶属程度是不完全一样的。供应商T4和T5的情况也类似。因此,有必要在评定各供应商风险等级的基础上,区分相同风险等级中各供应商之间的差异程度。
(一)二元语义的概念
2000年西班牙学者Herrerα教授首次提出了关于语言信息集结的二元语义分析方法[11],通过使连续化的语言信息表示语言评价信息并进行运算,可有效避免语言评价信息集结和运算中出现的信息损失和扭曲,也使语言信息计算结果更为精确。[12]二元语义算子评价决策方法已被应用于多目标决策以及多因素分析等研究领域[13],现将其发展、应用于风险等级评估。
前面定义的风险等级集E={e1,e2,…,eh}实际上就是1个语言短语集,其中的风险等级ek(k=1,2,…,h)表示语言短语“k级风险”,且根据事先规定的要求e1>e2>… >eh,即“k级风险”ek比“k+1级风险”ek+1强。换句话说,E={e1,e2,…,eh}是1个有序集。比如,1个3等级的风险等级集E={e1,e2,e3}可定义为:语言短语e1=“1级风险”即“风险很大”、e2=“2级风险”即“风险一般”、e3=“3级风险”即“风险很小”。通常,风险等级集E={e1,e2,…,eh}应满足有序性和极大化、极小化运算等。
若供应商Tj(j=1,2,…,n)的级别判定值为υj∈[1,h],则其二元语义可表示为二元有序组(ek,αjk),其中 ek∈ E 和 αjk∈[- 0.5,0.5),具体含义可描述为:(1)ek是事先已定义好顺序的E={e1,e2,…,eh}中的“k级风险”,表示由级别判定值 υj得到的、与E中最贴近的风险等级;(2)αjk是符号转移值,表示υj与由其得到的供应商Tj风险等级评估结果即k的偏差值(正、负号分别表示正负偏差)。
(二)风险等级评估二元语义方法的原理与步骤

若供应商Tj(j=1,2,…,n)的级别判定值υj满足条件则评定Tj为k级风险(即ek)供应商。为了刻画供应商属于k级风险的偏差程度,用偏差值表示为αjk= υj- k。显然,-0.5≤αjk< 0.5。αjk的含义是很清楚的。若 αjk∈[-0.5,0)越大(即越小),则υj∈(k -1,k)越大,且越接近于k,其相应供应商Tj也由属于k-1级风险逐渐降低到k级风险。反之,若αjk∈(0,0.5)越小,则υj∈(k,k+1)越小,且越接近于k,相应的Tj属于k级风险的程度也越大。若αjk=0,则υj=k,其相应供应商Tj正好属于k级风险。
对式(6),利用二元语义的概念可解释为:把供应商Tj的级别判定值υj表示为二元语义(ek,αjk),其中ek表示对Tj评定的风险等级、αjk表示υj与由其得到的供应商风险等级k的偏差值。用数学语言可描述为:存在 1个可逆映射 τ:[1,h]→ E ×[-0.5,0.5)使得

Round为四舍五入取整函数或算子。显然,τ的逆映射 τ-1:E ×[- 0.5,0.5)→[1,h]使得
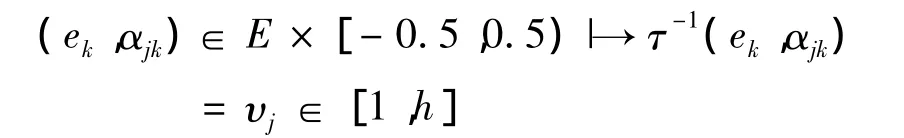
式中,υj=k+ αjk。设(ek,αjk)、(el,αil)分别是供应商Tj和Ti的级别判定值υj、υi的二元语义,规定其大小如下:(A)若ek>el(或k<l),则(ek,αjk)>(el,αil);(B)若 ek=el(或 k=l),则当:αjk= αil时,(ek,αjk)=(el,αil);αjk> αil时,(ek,αjk)<(el,αil);αjk< αil时,(ek,αjk) > (el,αil)。情况(A)表示,若供应商风险等级高,则不论其偏差值如何,其相应供应商风险级别判定值的二元语义大。而情况(B)表示,在供应商风险等级相同的条件下,供应商风险级别判定值的二元语义的大小取决于偏差值,偏差值越小,其相应的二元语义越大。于是,可根据二元语义(ek,αjk)对供应商Tj(j=1,2,…,n)进行风险等级评定和风险大小排序。具体方法与步骤如下:
第1步:利用式(7)和式(8)计算得到供应商Tj(j=1,2,…,n)风险级别判定值 υj的二元语义(ek,αjk);
第2 步:根据(ek,αjk)(j=1,2,…,n)确定所有n个供应商的风险等级,并按从大到小的顺序确定供应商风险大小排序,即:风险等级不同时,风险等级高(即ek大或k小)的供应商,其风险排序排在前面;风险等级相同时,其偏差值αjk小的供应商,其风险排序排在前面。
再考虑表1中各供应商的风险等级评估问题。利用式(7)和式(8)可算得供应商Tj(j=1,2,3,4,5)风险级别判定值υj的二元语义;利用二元语义的概念和大小比较关系,可确定所有供应商的风险等级和风险大小排序,如表2:
拿着一支百合的何西推门进咖啡厅,举目环视一眼看到一巨胖女孩单独坐在一张桌前一副等人的模样,就有一种不祥的预感,再往里面走了几步想看看还有没有别的女孩,这时胖女孩往门口这边张望,何西吓得慌不择路直往门口跑,跑到门口急忙掏出手机打电话:“何东,特胖……”

表2 供应商风险等级评估结果及排序
由表2可以看出,根据二元语义评定的供应商风险等级与由式(5)评定的有所不同,但直观上,前者的结果是比较合理的,且与前面的分析相吻合。因此,供应商Tj(j=1,2,…,5)的风险等级评估结果应该是:T1、T2和T3属于2级风险供应商,T4和T5属于3级风险供应商,且供应商风险排序为T1>T2>T3>T4>T5。
四、结束语
供应商风险等级评估实质上是一类特殊的多属性(或供应商、准则、因素、指标)综合评价(或决策)问题。在系统描述供应商风险等级评估模型的基础上,提出了供应商风险等级评估的级别判定值和二元语义概念,并建立了相应的供应商风险等级评估二元语义方法。该方法不仅可以合理地确定供应商风险等级,还可以区分相同风险等级供应商的风险大小即排序。二元语义的表示方式可为实现供应商风险等级评估结果的符号化运算提供理论基础,便于计算机实现,有利于针对性的进行供应商的风险控制管理,对现实供应链风险管理具有重要参考价值。
注释:
[1]William Ho,Xiaowei Xu,Prasanta K.Dey,“Multi- criteria decision making approaches for supplier evaluation and selection:A literature review”,European Journal of Operational Research,vol.202,no.1(2010),pp.16 -24.
[2]林勇、马士华:《供应商管理环境下供应商的综合评价选择研究》,《物流技术》2000年第5期。
[3]刘晓、李海越、王成恩:《储诚斌.供应商选择模型与方法综述》,《中国管理科学》2004年第1期。
[4]陈丽虹、胡宗武:《供应商风险管理中的排序问题》,《工业工程与管理》,2004年S1期。
[5]赵爱武、关洪军、石贵泉:《基于网络层次法的供应商风险评估指标》,《统计与决策》2013年第4期。
[6]丁斌、孙政晓、桂 斌:《基于粗糙集与未确知模型的供应商风险评估方法研究》,《中国管理科学》2008年第16期。
[7]陈新平:《紊乱环境下供应商风险预测模型》,《统计与决策》2011年第6期。
[8]Jennifer V.Blackhurst,Kevin P.Scheibe,Danny J.Johnson,“Supplier risk assessment and monitoring for the automotive industry”,International Journal of Physical Distribution & Logistics Management,vol.38,no.2(2008),pp.143 -165.
[9]刘庆广、施国洪:《基于供应链视角的供应商风险识别研究》,《价值工程》2009年第5期。
[10]李登峰:《模糊多目标多人决策与对策》,北京:国防工业出版社,2003年。
[11]Herrera F.,Herrera -Viedma E.,“Linguistic decision analysis:steps for solving decision problems under linguistic information”,Fuzzy Sets and Systems,vol.115,no.1(2000),pp.67 -82.
[12]Herrera F.,Herrera - Viedma E.,Martínez L.,“A fuzzy linguistic methodology to deal with unbalanced linguistic term sets”,IEEE Transactions on Fuzzy Systems,vol.12,no.2(2008),pp.354 -370.
[13]Li Deng-feng,“Multiattribute group decision making method using extended linguistic variables”,International Journal of Uncertainty,Fuzziness and Knowledge- Based Systems,vol.17,no.6(2009),pp.793 -806.

