Chirp信号的时频分析特征比较

周静雷，王 帆

（西安工程大学 陕西 西安 710048）

Chirp信号即线性调频信号是瞬时频率在某个范围内随时间变化的正弦波，因其良好的频带利用率，具有较强的抗干扰、抗多径效应和抗多普勒衰减以及良好的频带利用率等优点，因此在通信、声纳、雷达等领域具有广泛的应用。文中用各类时频分析方法 （主要是短时傅里叶变换、Wigner-Ville分布、小波变换、希尔伯特黄变换）分析chirp信号的特性，之后添加单频正弦噪声，运用Matlab仿真得到分析结果。

1 Chirp信号的时域波形以及FFT结果

设信号 x（t）的采样频率 fs为 48 000，扫描时间为 3，初始频率设为20，结束频率设置为20 000。用单频为2 000的正弦信号模拟噪声信号添加到原信号中进行仿真。其中N取1 024。

2 时频分析以及其结果

2.1 短时傅里叶变换（STFT）

短时傅里叶变换[1-2]的基本思想是用一个时间宽度足够窄的固定的窗函数乘时间信号，使取出的信号可以被看成平稳的，然后对取出的这一段信号进行傅里叶变换，便可以反映出该时间宽度中的频谱变化规律。

定义：对于给定的非平稳信号 x（t）∈L2（R），信号 x（t）的短时傅里叶变换定义为：

其中，h（t）成为窗函数。

分别用汉宁窗、高斯窗以及海明窗对信号x（t）求STFT，MATLAB仿真得到如图2所示。

从图2中可以看出短时傅里叶变换的结果受时窗函数的影响比较严重，对信号加汉宁窗时，可以获得好的时间分辨率，却得不到好的频率分辨率，而加汉明窗时，则相反，因此对于短时傅里叶变换，信号的时间与频率不能同时获得高的分辨力，在实际信号分析中，应该恰当地选取时间窗函数。

2.2 Wigner-Ville变换

WVD[3，5-6]分布是一种能量型的时频联合分布，具有别于其它时频分布优良的性质。

定义：对信号 x（t）的魏格纳-威尔分布定义为信号 x（t）的瞬时自相关的傅里叶变换，即

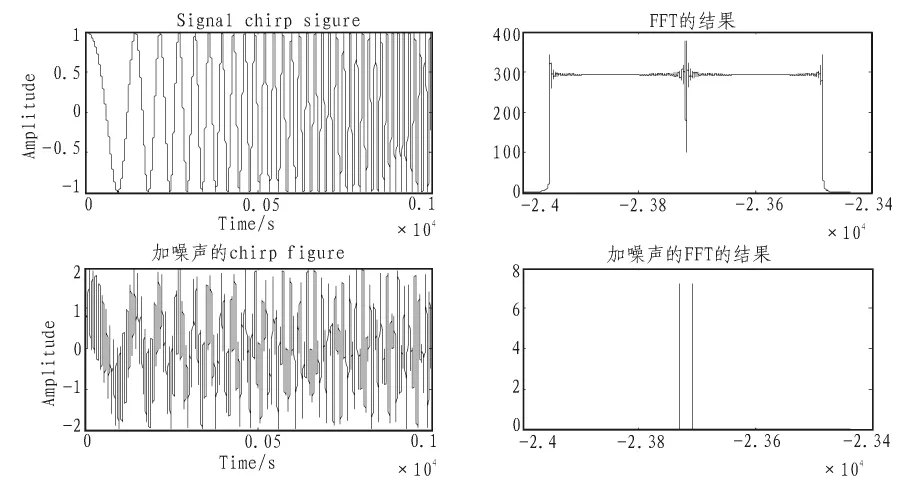
图1 信号时域波形以及傅里叶变换的结果Fig.1 Time domain waveform signal and FFT results

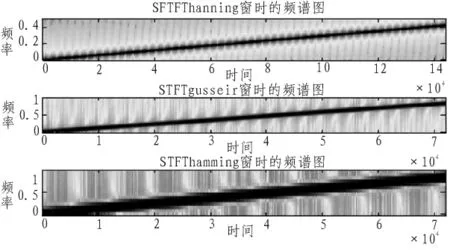
图2 加不同窗函数时的短时傅里叶变换图Fig.2 STFT with added the different windows

由图3可以看出WVD分布具有更好的分辨率和时频聚集度。其中由图下面部分可以看出WVD加噪声之后存在较强的交叉项干扰，不易分辨出噪声信号，因此在应用时，关键是如何设计核函数来抑制交叉项。

2.3 小波变换

定义：设{ψa，b}是一个满足条件的小波函数，对任意函数x（t）∈L2（R），它的小波变换定义为：从定义中可以看出连续小波ψa，b（t）的作用与短时傅里叶变换中的h（t）相似，起到窗函数的作用。

由图4可以直观的看出该信号频率随时间线性变化的情形，小波变换[4，7]具有对信号很强的自适应性，在高频段有较高的时间分辨率，在低频段有较高的频率分辨率，并且在时域和频域同时具有良好的局部化性质。由图的下半部分可以看出在处理单频噪声的时候，小波变换分辨力较低，几乎没什么变化。

2.4 希尔伯特黄变换

HHT变换[8-10]是为了得到适合Hilbert变换的信号而发展而来的一种新的信号处理方法。它主要包含两个部分，一是经验模态分解，也是最主要的部分，该部分的核心思想为本征模态函数，Huang创造性的提出了本征模态函数的概念，把复杂的信号分解成从高频到低频的的若干个固有模态函数（IMF：Intrinsic Mode Function）。 IMF 需具有以下两个特点：1）其极值点（极大值和极小值）数目与跨零点数目相等或最多相差一个；2）由其局部极大值构成的上包络和其局部极小值构成的下包络平均值为0。二是Hilbert谱分析，Hilbert变换应用久远，起先是由Euler公式发展而来的，信号经过Hilbert变换，可得到瞬时振幅、瞬时相位、瞬时频率等属性信息，进而得到Hilbert边际谱 。

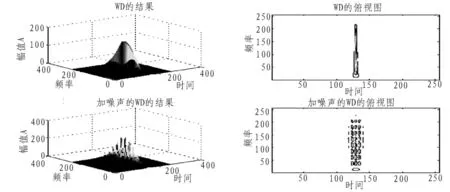
图3 Wigner-Ville分布图Fig.3 Wigner-Ville distribution

图4 小波变换的时频图Fig.4 Wavelet transform time-frequency diagram

由图5、6可知，EMD方法是按不同的时间尺度分解信号，先分解出高频，再分解出低频，次低频，最后得到趋势项。EMD分解是信号[11]本身所决定的一个自适应分解过程，能很快地提取信号特征并分解出信号的分量。图6中可以看出，imf1和imf2刚好是原信号和添加的正弦信号，体现了分解的可靠性以及IMF的物理意义。

由图7、8可知Hilbert[12]谱的大部分能量都集中在一定的时间和频率范围内，从图8中可以很清楚地看出添加的正弦噪声，因此该分析方法在处理chirp信号中掺杂的单频噪声有一定的优势。

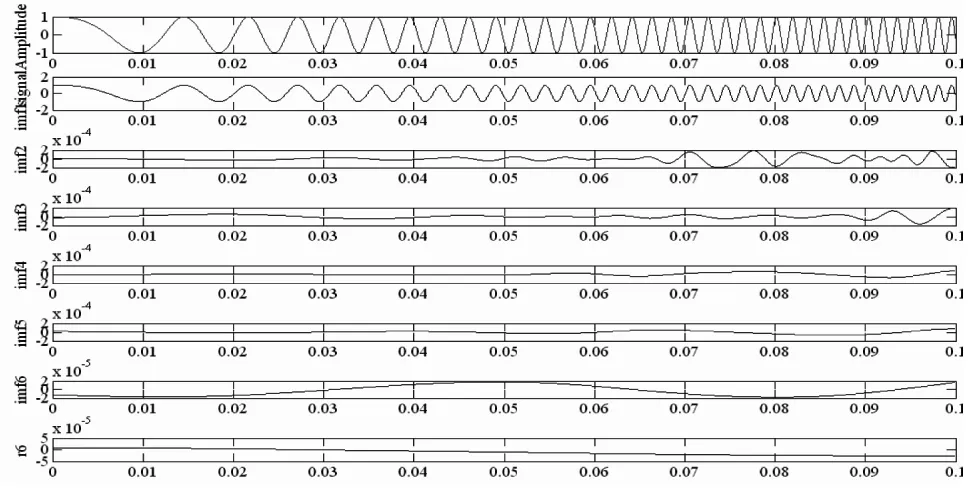
图5 EMD分解图Fig.5 EMD decomposition map

图6 加噪声的EMD分解图Fig.6 EMD decomposition map added noise

图7 HHT时频图Fig.7 HHT time-frequency diagram

图8 加噪声的HHT时频图Fig.8 HHT time-frequency diagram added noise

3 结 论

通过上述的仿真分析比较可以看出，短时傅里叶变换简单，通俗易懂，但是处理信号的时候不能同时保证时间和频率分辨率高，WVD分布有较好的时频聚集性，但是在处理有单频噪声信号的时候，分辨率很低，小波变换具有较好的局部分辨率，但是处理单频噪声也几乎分辨不出来，而希尔伯特黄变换除了具有较好的分辨率之外，在处理单频噪声具有很好的分辨率，在HHT谱中就可以明显看出，因此在处理非平稳信号的时候，选择HHT黄变换，是一种比较有效的方法。

[1]董建华，顾汉明，张星.几种时频分析方法的比较及应用[J].工程地球物理学报，2007，4（4）:312-316.DONG Jian-hua，GU Han-ming，ZHANG Xing.Several kinds of time-frequency analysis method comparison and application[J].Engineering Geophysical Journal，2007，4（4）:312-316.

[2]葛哲学，陈仲生.Matlab时频分析技术及其应用[M].北京:人民邮电出社，2006.

[3]张威斌，曹继华，等.两种时频分析算法的分析比较[J].工程技术，2011，12（3）:79-82.ZHANG Wei-bin，CAO Ji-hua，et al.Two kinds of timefrequency analysis algorithm are analyzed and compared[J].Engineering Technology，2011，12（3）:79-82.

[4]苏凯，蒋宇中，等.Chirp信号的去噪研究及其Matlab实现[J].通信技术，2011，7（44）:51-53.SUKai，JIANGYu-zhong，et al.Chirp signal denoising research and the realization of Matlab[J].Communication Technology，2011，7（44）:51-53.

[5]万建伟，王玲.信号处理仿真技术[M].长沙:国防科技出版社，2008.

[6]石波涌，苏凯，邓铁辉，等.一种基于 chirp信号的去干扰算法[J].无线通信技术，2011（4）:14-16.SHI Bo-yong，SU Kai，DENG Tie-hui，et al.A method based on chirp signal to interference algorithm[J].Wireless Communication Technology，2011（4）:14-16.

[7]LI Hong-bing，ZHAO Wen-zhi，et al.Measures of scale based on the wavelet scalogram with applications to seismic attenuation[J].Geophysics，2006，71（5）:111-118.

[8]Wu Z H，Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis，2009（1）:1-41.

[9]王伟.Hilbert-Huang变换及其在非平稳信号分析中的应用研究[D].北京:华北电力，2008.

[10]Rilling G，Flandrin P.On the influence of sampling on the Empirical Mode Decomposition[C]//in Proc.IEEE Int.Conf.on Acoust，Speech and Signal Proc.ICASSP-06，Toulouse （F），2006.

[11]李玲俐.智能保健监测系统中音频信号的分类算法研究[J].重庆师范大学学报:自然科学版，2012（4）：73-76.LI Ling-li.Audio signal classification agorithm for a smart health-Care monitoring system[J].Journal of Chongqing Normal University：Natural Science，2012（4）：73-76.

[12]陈广生，丁宣浩.一个新的Hilbert型积分不等式[J].重庆师范大学学报:自然科学版，2011（1）：37-39.CHEN Guang-sheng，DING Xuan-hao.A new Hilbert’s type integral inequality[J].Journal of Chongqing Normal University：Natural Science，2011（1）：37-39.