0.5 THz二次谐波同轴回旋管的设计

雷蕾

（电子科技大学 物理电子学院，四川 成都 610054）

回旋管是一种基于自由电子受激辐射原理的新型电真空器件，可应用于等离子体诊断、电子自旋共振、通信、新医疗技术等多方面[1-2]。目前，回旋管最高工作频率已可达到1 THz。然而随着回旋管工作频率的升高，对磁场的要求也越来越高，磁场的造价也越来越高，这就限制了太赫兹频段回旋管的应用空间。当回旋管采用l高次谐波工作时其所需的工作磁场仅为基模的1/l，这将极大地降低对工作磁场的需求。美国、日本、俄罗斯等多个国家和地区都进行了高次谐波回旋管的研制工作，美国麻省理工学院研制的低功率高次谐波回旋管主要用于动态核极化研究，俄罗斯国家科学院应用物理研究所和日本福井大学近期实验的高次谐波回旋管输出功率可达千瓦级。我国电子科技大学近期进行的二次谐波回旋管实验输出功率可达4.4 kW。文中设计了一支二次谐波回旋管，极大降低了对工作磁场的要求，选用模为工作模式，其工作电压为49 kV，工作电流为5 A，工作磁场为9.64 T电子注横纵速度比为1.5，经过多次优化，其效率为22.52%，输出功率可达55 kW。

1 物理模型

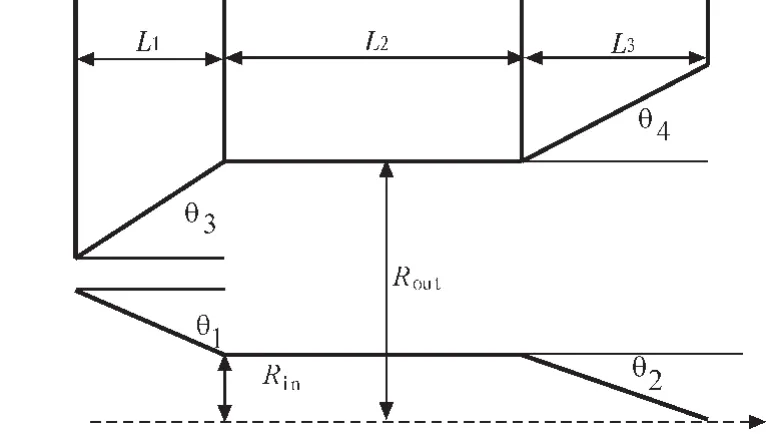
图1 同轴谐振腔结构图Fig.1 Coaxial resonator structure

工作在高次谐波的回旋管竞争模式将急剧增加，同轴谐振腔与传统的圆柱谐振腔相比，能够较好地克服模式竞争，并且能够更好地解决电子注电压下降问题。文中采用三段式结构同轴谐振腔，如图1所示。对于给定的工作频率，回旋管工作模式越低其所要求的腔体尺寸越小，尺寸越小则越难于加工，而当工作模式过高时，模式竞争将非常剧烈。文中采用TE56模为工作模式，各项结构参数如表1所示。

表1 同轴谐振腔结构参数Tab.1 Coaxial resonator structure parameter

2 模拟计算

2.1 起振电流分析

二次谐波回旋管模式竞争比较严重，可以通过选择合适的引导中心半径和起振电流加以克服。图2给出了耦合系数与电子注引导中心半径的Re关系，考虑到电子回旋半径等因数，选择Re=1.72 mm是较为合适的。由线性理论，同轴回旋管起振电流：

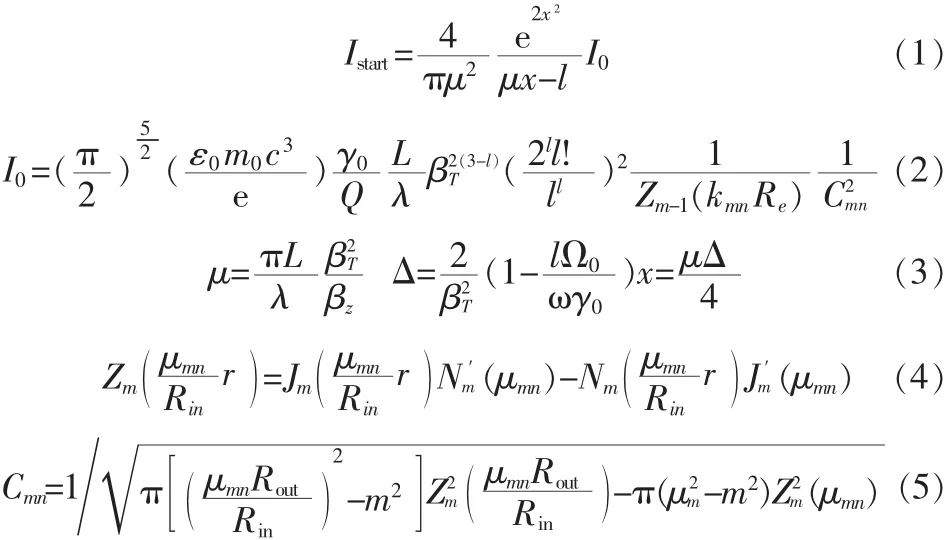
式（1）～（5）中，kmn为本征值，μmn=kmnRin，β=v/c，Jm和 Nm分别代表m阶第一类贝塞尔函数和m阶第二类贝塞尔函数。工作电压为49 kV，Re=1.72 mm，电子横纵速度比为1.5时各个模式起振电流如图3所示，当选取的工作磁场在9.7 T附近时，可有效地克服其他竞争模式。

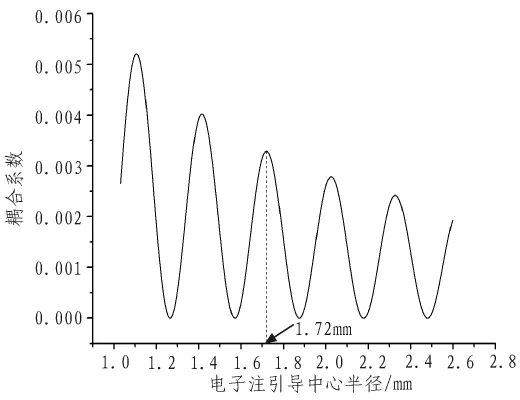
图2 耦合系数Fig.2 Coupling coefficient

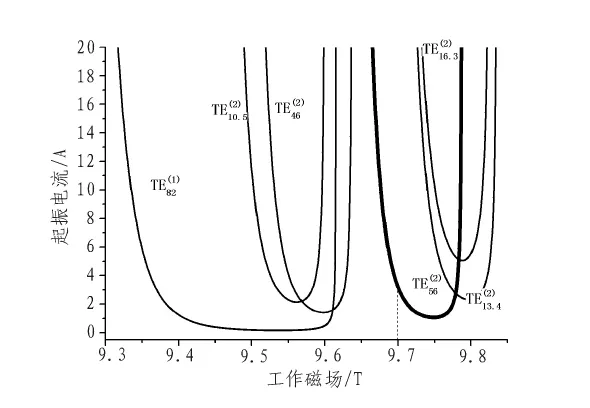
图3 起振电流Fig.3 Starting current

2.2 注波互作用分析

自洽非线性理论考虑了电磁场对电子的作用和电子对电磁场的反作用，在假定单一模式稳定工作的条件下，可以研究多种工作条件对电子注波互作用的影响，从而可以优化相关参数，使回旋管效率达到最佳。文中采用回旋管自洽非线性理论进行注波互作用分析，对注波互作用效率与中间段腔长、工作磁场、电压和电流的关系进行了研究，如图4－图7所示。当固定工作电压为49 kV，电流为5 A，工作磁场为9.66 T时，不同中间段腔与注波互作用效率关系如图4所示。效率随着中间段腔长的增加而增加，谐振频率随着中间段腔长增加而降低。当中间段腔长mm，效率达到最大。当腔长过大时，电场角频率将小于电子的回旋频率，从而影响注波互作用效率。

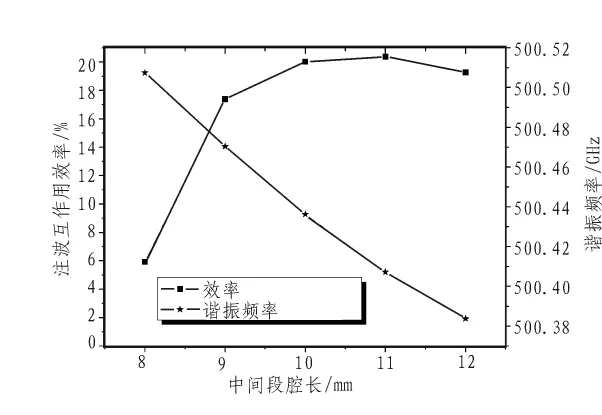
图4 中间段腔长与注波互作用效率关系Fig.4 Efficiency with the middle segment length

图5 为工作电压为49 kV，电流为5 A时所作的磁场与注波互作用效率图，在一定范围内，效率将随着磁场的的升高而升高，当超过最佳值时，将随着磁场的升高而降低。这是因为电子要把能量交给电磁波，必须将大部分电子置于减速场中，即电场的角频率应稍大于电子的回旋频率，而磁场与电子回旋频率成正比，当磁场过大时，电子的回旋频率将大于电场的角频率，从而影响电子交出能量。由图4可知，当工作磁场为9.64 T时，效率达到最高。

图5 工作磁场与注波互作用效率关系Fig.5 Efficiency with operating magnetic field

图6 为工作磁场为9.64 T，电流为5 A时作的电压与注波互作用效率图。电压为49 kV时，效率达到最佳，电压与效率变化关系规律与磁场类似，但是电压与电子回旋频率近似呈反比关系，当电压过大时，电子回旋频率会过小，不再满足回旋谐振基本条件继而影响效率。

电流与注波互作用效率关系图如图7所示，选定工作电压为49 kV，工作磁场为9.64 T。由图可知，当电流增大时，效率将最随着电流的增大而增加，当电流为5 A时，效率达到最大值，随后效率将随着电流的增大缓慢变小。综合以上分析，当选定各项工作参数如表2所示时，回旋管将达到一个较佳状态。

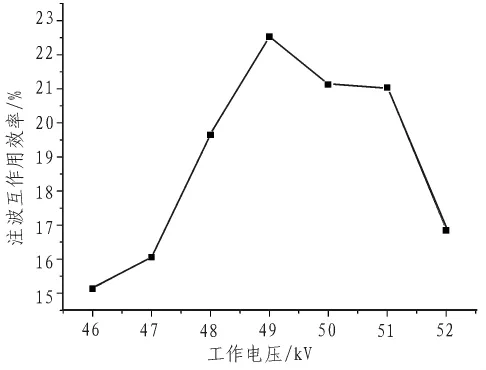
图6 工作电压与注波互作用效率关系Fig.6 Efficiency with operating voltage

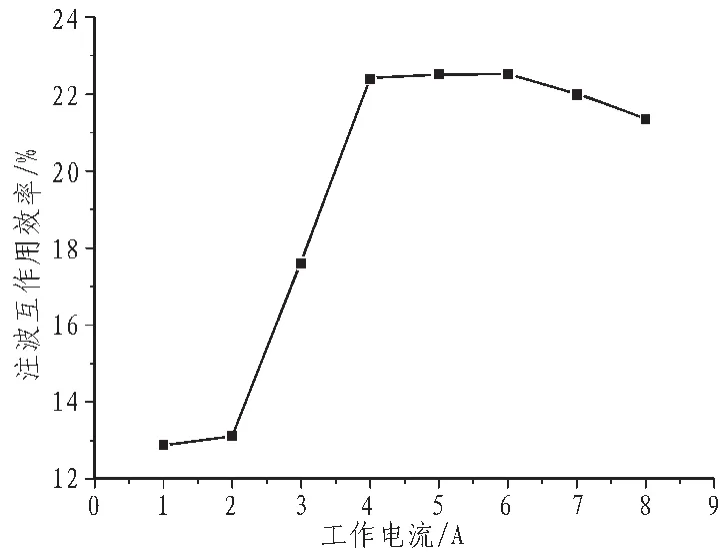
图7 工作电流与注波互作用效率关系Fig.7 Efficiency with operating current

3 结 论

文中基于回旋管线性理论和自洽非线性理论设计了一支0.5 THz二次谐波回旋管，研究了中间段腔长、工作磁场、电压和电流对注波互作用效率的影响，充分优化了各项参数，经过优化后的结构参数和各项工作参数如表1和表2所示，效率为22.52%，输出功率可达55 kW。采用二次谐波工作模式，使所需工作磁场仅为基模的一半，极大地减少了磁场的造价，具有一定的实用性，也为二次谐波回旋管的设计提供了一定的参考。

[1]Notake T，Saito T，Tatematsu Y，et al.Development of a novel high power sub-THz second harmonic gyrotron[J].Phys.Rev.Lett，2009，103（22）:225002.

[2]Glyavin M Y，Luchinin A G，Golubiatnikov.Generation of 1.5 kW，1-THzcoherent radiation from a gyrotron with a pulsed magnetic Field[J].Phys.Rev.Lett，2008，100（1）:15-101.

[3]Hornstein M K，Bajaj V S，Griffin R G，et al.Second harmonic operation at 460 GHz and broadband continuous frequency tuningof agyrotron oscillator[J].IEEETransactionson Electron Devices，2005，52（5）:798-807.

[4]Bratman V L，Bogdashov A A， Denisov G G，et al.Gyrotron development for high power THz technologies at IAPRAS[J].JInfrared Milli Terahz Waves，2012（33）:715-723.

[5]Saito T，Yamada N，Ikeuti S，et al.Generation of high power sub-terahertz radiation from a gyrotron with second harmonic oscillation[J].Physics of Plasmas，2012.

[6]FU Wen-jin，YAN Yang，LI Xiao-yun，et al.Generating 0.42THz radiation from a second harmonic gyrotron[J].Chinese Science Bulletin，2011，56（33）:3572-3574.

[7]喻胜，李宏福，谢仲怜，等.渐变复合腔回旋管高次谐波注波互作用非线性模拟[J].物理学报，2000，49（12）：2455-2459.YU Sheng，LI Hong-fu，XIE Zhong-lian，et al.A nonlinear simulation on beam-wave interaction for high-harmonic complex cavity gyrotron with gradual transition[J].Acta Physica Sinica，2000，49（12）：2455-2459.

[8]Generalized Nonlinear Harmonic Gyrotron Theory[J].Phys.Fluids，1986，29（2）:561-567.

[9]Agusu L，Idehara T，Dumbrajs O.Mode selection for a terahertz gyrotron based on a pulse magnet system[J].International Journal of Infrared and Millimeter Waves，2004，25 （7）：1023-1035

[10]刘盛纲.相对论电子学[M].北京：科学出版社，1987.