具有不同转子匝数的新型双馈风力发电机低电压穿越能力的瞬态性能分析
蒋 毅 黄晓艳
(浙江大学电气工程学院 杭州 310027)
1 引言
随着风力发电技术的不断发展,风力发电在电网中所占的比重不断增加,风力发电技术也受到了各国专家学者的广泛关注[1]。在众多方案中,双馈式风力发电机(Doubly Fed Induction Generation,DFIG)凭借其变流器容量相对较小[2],解耦功率控制简单[3]、成本较低等各项优点,成为目前市场上兆瓦级容量的主要风电机型[4,5]。
然而,在电网电压跌落时,双馈风力发电机容易出现励磁失控,转子电流迅速升高。若不采取措施,该电流将会危害系统变流器,使电机转速急剧升高,当达到极限转速时,将会引发刹车系统动作,使电机从电网解列[6]。进而,将减少风电场对电网的有功和无功支持,使电网电压进一步跌落,产生连锁反应。因此,如何实现双馈风力发电机的低电压穿越(Low Voltage Ride Through, LVRT)能力成为风力发电行业急需解决的技术问题 。
目前,双馈风力发电机主要通过两种方法实现LVRT能力,一种是改进现有控制算法实现,另外一种是硬件电路实现。文献[8]从抑制转子电流中旋转分量的角度出发,省去了定子磁链观测,提出简化后的DFIG控制算法。文献[9]提出了一种基于定子磁链跟踪的LVRT控制策略,通过转子磁链实时地跟踪补偿定子磁链以抑制故障电流,此法理论得以证明,但不利于工程实现。文献[10]针对现有主动式Crowbar电路的不足,提出旁路阻值优化整定方法。但是,实验发现控制算法只能针对小范围电压跌落,而硬件电路实现功耗较大[11],两种方法都存在一定缺陷。
本文在电压跌落瞬态过程中双馈电机的动态分析基础上,通过变换转子绕组匝数实现LVRT能力,并建立能切换转子绕组的DFIG模型,进行仿真分析和样机系统测试,结果证明该技术方法行之有效。
2 新型DFIG模型
变速恒频双馈风力发电系统如图1所示。发电机采用三相绕线式异步发电机,定子与三相电网直接相连,转子通过背靠背结构 PWM变流器与电网相连,从而实现交流励磁,可调整励磁电压幅值和电机转速[12]。变流器能实现双向功率流动,对双馈电机进行有功和无功的解耦控制。
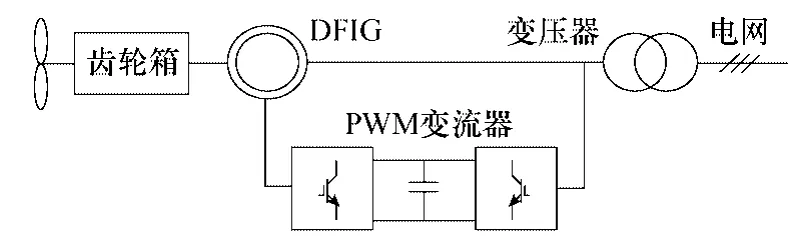
图1 变速恒频双馈风力发电系统Fig.1 The variable speed constant frequency doubly-fed wind power generation system
其中,在稳态正常工作情况下,转子电压矢量和感应电动势幅值表达式[13]为
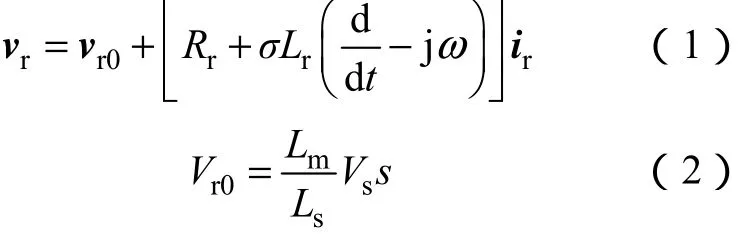
在三相电网电压跌落时,转子感应电动势幅值表达式[13]为
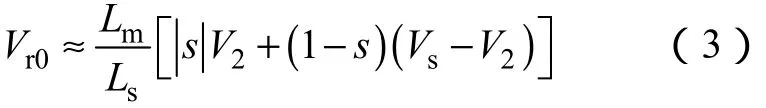
式中vr——转子电压矢量;
vr0——转子感应电动势矢量;
ir——转子电流矢量;
Vs——原电网电压幅值;
V2——电网电压跌落后电压幅值;
Rr——转子电阻;
Ls——定子自感;
Lr——转子自感;
Lm——定、转子之间等效互感;
σ——漏感系数;
ω——转子转速;
s——转差率。
可以发现在电压跌落前,转子感应电动势Vr0∝sVs。电压跌落时,转子感应电动势受电压跌落幅值Vs-V2和转差率s两个值影响较大。
分析可知,在电压跌落过程中,vr0幅值将会升高,转子侧端电压将会发生显著变化。若vr0幅值大于变流器所能承受的电压幅值,电流则将会失控,并迅速增大,严重危害变流器,进而导致转子失速、电机退网等一系列问题。故低电压穿越实现的根本问题,在于电网电压跌落时,减小转子vr0的幅值,使其在变流器的控制范围以内。本文从减小转子感应电动势vr0的角度出发,分析改变转子绕组匝数对电网电压跌落瞬态性能的影响。
图2为转子绕组匝数能够切换的DFIG原理图。该 DFIG电机定子三相绕组与普通感应电机相同,而转子绕组虽也为三相,但每相绕组有两个端部抽头,即abc与a′b′c′两组抽头。在正常工作状态中,转子选用 abc三相抽头,电机工作与普通DFIG相同;当发生电网电压跌落时,立即切换转子绕组为a′b′c′抽头,使电机绕组有效匝数减少,降低了转子感应电动势vr0,使其在变流器控制范围以内,从而抑制转子回路电流的上升。

图2 转子绕组匝数能够切换的DFIG结构Fig.2 The model of DFIG with capacity of changing the number of the turns of the rotor windings
3 新型DFIG建模与仿真分析
由矢量变换原理可以知道,在定子两相静止坐标系下,定、转子磁链方程 为
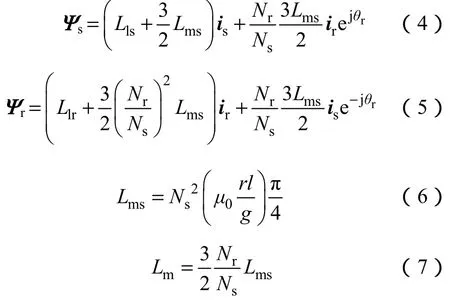
式中Ψs——定子磁链;
Ψr——转子磁链;
Lls——定子侧漏感;
Llr——转子侧漏感;
Lms——定子侧互感;
Ns——定子绕组有效匝数;
Nr——转子绕组有效匝数;
θr——转子角度;
r——定子半径;
g——气隙长度;
l——定子长度;
μ0——磁导率。
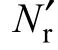

由式(3)可知,若转子绕组在电压跌落过程中立刻切换绕组,则可以得到,在电压跌落时
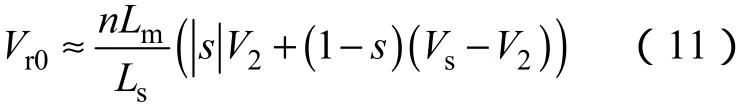
DFIG电机转子有效部分变化,引起电感和匝数比两项参数变化,降低了转子内部感应电动势Vr0,使幅值在变流器控制电压以内,以达到抑制电流增大的目的。
3.1 全电压跌落情况分析
本文建立了转子绕组匝数能够切换的 DFIG的Matlab仿真模型,额定功率为 7.5kW。定子电阻Rs=0.45Ω;转子电阻Rr=0.2Ω;定子漏感Lls=0.01H;转子漏感Llr=0.007H;互感Lm=0.088H。
图 3为三相电网电压全跌落时,DFIG在绕组切换与不切换条件下的定子电压、定子电流、转子电流波形。
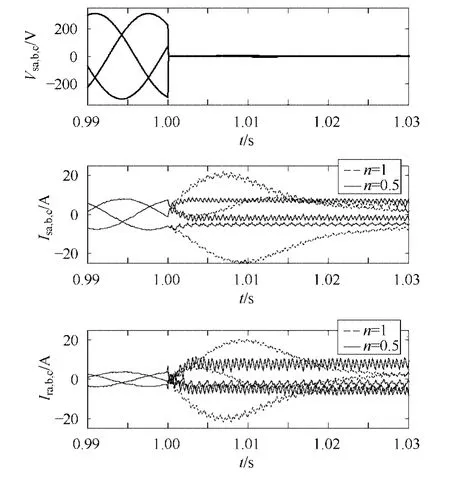
图3 DFIG绕组切换与不切换条件下参数波形(nspeed=1 450r/min, n=0.5,全电压跌落)Fig.3 The DFIG waveform parameter in changing and nonchanging winding situation(nspeed=1 450r/min, n=0.5, full voltage dip)
在 0~1s时,电机拖动额定负载工作在nspeed=1 450r/min下运行;1s时,电网发生三相全电压跌落,定子端电压降低至 0。图3中,虚线为不切换绕组的 DFIG参数波形,在电网全电压跌落时,其定子电流Isa,b,c和转子电流Ira,b,c迅速上升,Isa,b,c三相最大幅值达25A,Ira,b,c三相最大幅值达23A;实线为 1s时切换为部分绕组(n=0.5)的 DFIG参数波形,在同样情况下,定子电流Is′a,b,c上升最高至8A,Ir′a,b,c上升最高至 9A。
通过图3波形比较可以看出,相比n=1(不切换绕组)的情况而言,DFIG在全电压跌落时立刻切换绕组为n=0.5后,定、转子电流上升较为缓慢,幅值相对较低,并且几乎维持在定、转子额定电流附近,从而很大程度减小了转子电流对变流器的冲击,实现了低电压穿越能力。
如图4所示,选取了五组不同n值(分别为0.1,0.3, 0.5, 0.7, 0.9)进行仿真,得到A相转子电流大小,并以此和n=1(不切换绕组)的 DFIG相应时刻A相转子电流进行参考比较。
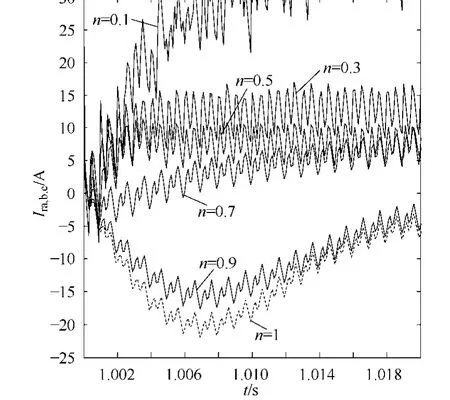
图4 转子n变化对于新型DFIG转子电流的影响(nspeed=1 450r/min,电压全跌落)Fig.4 n for the influence on the DFIG rotor current(nspeed=1 450r/min, full voltage dip)
n分别取0.3、0.5、0.7、0.9时,该电机的A相转子电流都小于20A,即小于不切换情况下的A相电流幅值。而当n=0.1时,切换转子绕组后 DFIG的 A相转子电流大大增加,达到 30A以上,超过n=1情况下的最大幅值。值得一提的是,取n=0.5时,能始终使转子电流保持在10A以下,能够最好地实现LVRT能力。所以,n=0.5是全电压跌落情况下n的最优值。
3.2 部分电压跌落情况分析
在电力系统实际运行中,部分电压跌落经常发生,由于系统负荷的变化、变压器的投切等都会引起电网电压的波动,甚至引起部分电压跌落。因此下文将针对部分电压跌落情况进行研究。

通过仿真比较可以看出,相比n=1情况,切换绕组(n=0.5)的 DFIG,同样能够在电压部分跌落发生后,达到抑制转子电流增加的目的,实现低电压穿越。
根据上文理论分析,部分电压跌落情况下n的最优取值,应该与全电压跌落情况下的n的最优值有所不同。下文将针对电压部分跌落(70%)情况下,讨论n的最优取值。
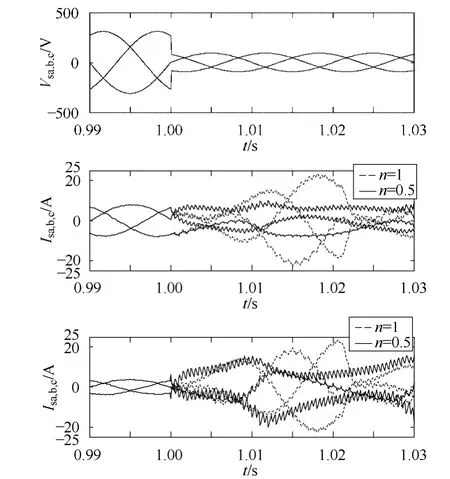
图5 DFIG绕组切换与不切换条件下参数波形(nspeed=1 450r/min, n=0.5,电压跌落70%)Fig.5 The DFIG waveform parameter in changing and nonchanging winding situation(nspeed=1 450r/min, n=0.5, 70% voltage dip)
如图6所示,仿真分析选取了新型DFIG的五组不同n值(分别为0.1, 0.3, 0.5, 0.7, 0.9),检测A相转子电流大小,并以此和n=1情况下相应时刻的A相转子电流进行参考比较。在1s时,电网电压发生三相电压部分跌落(跌落幅值 70%),根据n取值不同分别实验。n=1的 DFIG在电压跌落后,A相转子电流Ira达到19A。而1s时切换转子的DFIG,在n分别为0.3、0.5、0.7、0.9时,A相转子电流最大幅值都小于未切换绕组的DFIG。在n=0.1时,A相转子电流将大于未切换绕组 DFIG的相应电流幅值,并且达到20A以上。比较后发现,电网电压跌落70%时,取n=0.7效果最佳,转子电流幅值在7A以内。因此,在电压跌落70%时,n=0.7为最优值,与全电压跌落情况不同。

图6 转子n变化对于新型DFIG转子电流的影响(nspeed=1 450r/min,电压跌落70%)Fig.6 n for the influence on the DFIG rotor current(nspeed=1 450r/min, 70% voltage dip)
从结果可以看出,不同电压跌落情况下,绕组匝数对电机性能影响均有所不同。
4 新型DFIG低电压穿越测试系统
为了验证系统的有效性,对额定功率为 7.5kW的DFIG系统进行了相应测试。图7为测试系统结构原理图。直流电机驱动 DFIG模拟动力输入。当传感器检测到电网电压跌落后,将信号传输给FPGA,拓扑结构切换转子绕组有效匝数。DSP实现相应的数据记录和控制算法。
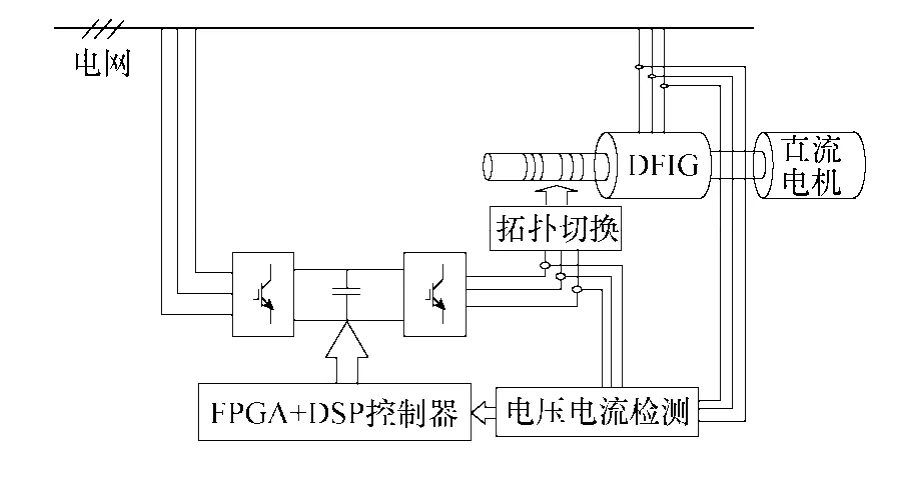
图7 7.5kW的DFIG测试系统结构原理图Fig.7 The schematic diagram of 7.5kW DFIG test system
本文对能进行转子切换的新型 DFIG低电压穿越能力进行了测试,电压选取跌落80%,图8为测试系统DSP数据采集波形。测试过程中,测试电机始终用直流电机拖动,转速保持 1 440r/min。为模拟实际电网的电压跌落和恢复过程,电网电压变化过程如下:在2.36s时,电网电压跌落80%;在3s时,电网电压缓慢上升;在 3.80s时,电网电压完全恢复。从测试结果来看,系统在检测到电压跌落后,迅速切换转子绕组为n=0.4,使得电流幅值在达到28A后迅速下降并维持。在3.43s时,控制系统再次切换绕组为全绕组状态,可以看出转子电流在短暂的振荡后迅速恢复。
从上述实验可以看出,本文所提出的新型DFIG能够有效实现低电压穿越。在实际运行过程中,采用特定的n值来实现低电压穿越,虽然很多情况下并不是最优值,但是测试证明能够满足系统实现低电压穿越的要求。
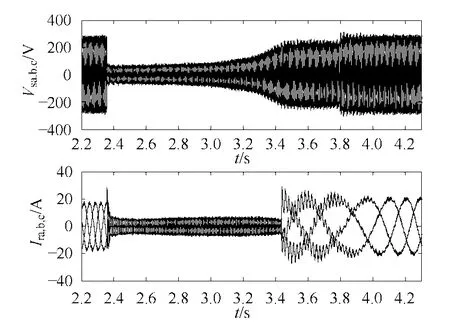
图8 DSP数据采集波形(nspeed=1 440r/min, n=0.4,电压跌落80%)Fig.8 The data acquisition waveforms from DSP(nspeed=1 440r/min, n=0.4, 80% voltage dip)
5 结论
本文分析了转子绕组变化对双馈电机低电压穿越瞬态性能的影响,详细论述了该结构电机的建模方法,并且对匝数变化参数n进行了分析研究。仿真证明,通过转子绕组的有效匝数变化,能够抑制电压跌落过程中的定、转子电流增大。在此基础上,本文给出了7.5kW的样机测试结果,论证了该方法能有效实现低电压穿越。
[1] 杨耕, 郑重. 双馈型风力发电系统低电压穿越技术综述[J]. 电力电子技术, 2011, 45(8): 32-36, 59.Yang Geng, Zheng Zhong. Review of low voltage ride-through technology for doubly-fed induction generator based wind energy conversion systems[J].Power Electronics, 2011, 45(8):32-36, 59.
[2] Nian H, Song Y P, Zhou P, et al. Improved directed power control of a wind turbine driven doubly fed induction generator during transient grid voltage unbalance[J]. IEEE Transactions on Energy Conversion,2011, 26(3):976-986.
[3] 胡胜, 林新春, 康勇, 等. 一种双馈风力发电机在电网电压不平衡条件下的改进控制策略[J]. 电工技术学报, 2011, 26(7): 21-29.Hu Sheng, Lin Xinchun, Kang Yong, et al. An improved control strategy of doubly-fed induction generator under grid voltage unbalance[J]. Transactions of China Electrotechnical Society, 2011, 26(7):21-29.
[4] 李建林, 朱颖, 胡书举, 等. 风力发电系统中大功率变流器的应用[J]. 高电压技术, 2009, 35(1): 169-175.Li Jianlin, Zhu Ying, Hu Shuju, et al. Topology and modulation strategy for high power converter in wind power system[J]. High Voltage Engineering, 2009,35(1): 169-175.
[5] 撖奥洋, 张哲, 尹项根, 等. 双馈风力发电系统故障特性及保护方案构建[J]. 电工技术学报, 2012,27(4): 233-239.Han Aoyang, Zhang Zhe, Yin Xianggen, et al.Research on fault characteristic and grid connectingpoint protection scheme for wind power generation with doubly-fed induction generator [J]. Transactions of China Electrotechnical Society, 2012, 27(4): 233-239.
[6] 秦原伟, 刘爽. 基于 Crowbar的双馈风力发电低电压穿越研究[J]. 电力电子技术, 2011, 45(8): 51-53.Qin Yuanwei, Liu Shuang. Doubly-fed induction generator low voltage ride through based on crowbar circuit[J]. Power Electronics, 2011, 45(8): 51-53.
[7] Ibrahim A O, Nguyen T H, Lee D C, et al. A fault ride-through technique of DFIG wind turbine system using dynamic voltage restorers[J]. IEEE Transactions on Energy Conversion, 2011, 26(3): 871-882.
[8] 蔚兰, 陈宇晨, 陈国呈, 等. 双馈感应风力发电机低电压穿越控制策略的理论分析与实验研究[J]. 电工技术学报, 2011, 26(7): 30-36.Yu Lan, Chen Yuchen, Chen Guocheng, et al. A low voltage ride-through control strategy of doubly fed induction generator[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 30-36.
[9] Xiao S, Yang G, Zhou H. A LVRT control strategy based on flux tracking for DFIG-based wind power systems[C]. IEEE Transactions on Energy Conversion,2011: 76-82.
[10] 孔宪国, 刘宗歧. 基于主动式 Crowbar的双馈风电机组LVRT性能优化分析[J]. 现代电力, 2012, 29(1):77-81.Kong Xianguo, Liu Zongqi. Analysis on LVRT performance optimization of DFIG with active crowbar[J]. Modern Electric Power, 2012, 29(1): 77-81.
[11] 张建华, 王健, 陈星莺, 等. 双馈风机低电压穿越控制策略的分析与研究[J]. 电力系统保护与控制,2011, 39(21): 28-33.Zhang Jianhua, Wang Jian, Chen Xingying, et al.Analysis of DFIG-based wind generation LVRT control strategy[J]. Power System Protection and Control, 2011, 39(21):28-33.
[12] Islam M R, Guo Y G, Zhu J G. Steady state characteristic simulation of DFIG wind power system[C]. IEEE Transactions on International Conference on Electrical & Computer Engineering,2010: 151-154.
[13] Lopez J, Sanchis P, Roboam X, et al. Dynamic behavior of the doubly fed induction generator during three-phase voltage dips[J]. IEEE Transactions on Energy Conversion, 2007, 22(3): 709-717.
[14] Novotny D W, Lipo T A. Vector control and dynamics of AC drives[M]. United States: Oxford University Press Inc, 1996.

