一个选用非织造隔热材料的实用模型
Idris Cerkez,Hasan B.Kocer,Roy M.Broughton 著
李桂梅 译 李燕立 校
0 简介
从一般的住宅到航天器,在很多结构上都使用隔热材料。在所有的应用中,隔热的目的都是为减少热传递,避免热量从一个表面散发到另一个表面。不管来源如何,热传递分为传导、对流和辐射三种机理,其中只有热传导比较容易用公式表示,而且也只是对平面材料而言。实用的方程就是Fourier热传导方程:
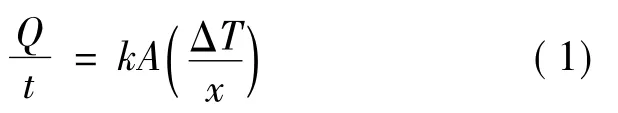
式中:Q——传递的热量(Btu,1 Btu=1 055.06 J);
t——时间 (h);
k——热导 率 [Btu· in/(h· ft2·℉),1 Btu·in/(h·ft2·℉)=0.144 W/(m·K)];
A——面积 (ft2,1 ft2=0.092 9 m2);
ΔT——温度差[℉,1℉ =(5/9)K];
x——厚度 (in,1 in=0.025 4 m)。
传热系数可以使用很多单位,但是在真正的工程中Btu·in/(h·ft2·℉)最为直观。其他的方程式使用面积除以厚度,以此减少了一个长度参数。W/(m·K)是一个在公制单位中描述热传递的通用单位(译者注:我国称该单位为热导率,亦称为导热系数)。在本研究中单位选用Btu·in/(h·ft2·℉),在进一步的分析中使用兼容的单位,选择这一点的原因是美国的建筑行业应用这一单位。热阻“R”用来标注所有的建筑部位,包括墙、地板和天花板的保温性能。
通常热阻“R”的测量首选热导率。热阻的计算是用隔热材料的厚度除以热导率。通常三种传热机理被总括为一个概念,称为表观传热系数,用上述热传导的方法一并处理。有效隔热的设计,就是克服三方面热能的传递。
对于纤维状隔热材料,可以通过增加密度来减少辐射的能量,因为密度增加会减少辐射量子运动的平均自由路程。平均自由路程定义为一个辐射量子在碰到另一个纤维表面前所走过的距离[1]。另一个近似方法是增加表面积,以此来增加辐射能的散射和吸收[2]。至于对流能量的传递,因为流道的弯曲和狭窄,可以认为没有流体流动(静止空气),因此可以被忽略[3]。早期的研究表明,在纤维结构的体积密度大于20 kg/m3(1.25 lb/ft3)时,对流(自然的)能量可以被忽略,因为空气分子的运动受到了纤维所构成的极小孔穴的限制[4]。热量通过传导方式传递时有两个机理:通过固体传导和通过气体传导。在空气的氛围里,隔热材料的热导率下限是在静止空气条件下的数值,该值在室温下是0.024 W/(m·K)[0.17 Btu·in/(h·ft2·℉)][5]。有证据表明,如果隔热材料的孔径小于空气分子的平均自由路径,则下限值还可以更低[6]。这一下限值可以通过抽真空或者更换导热性更低的气体(如二氧化碳或氢氯氟烃等)还能更低[7-8]。通过固体传导的热量与材料的热导率成正比,因此用纤维状材料隔热时,最佳材料的选择就成了关键。
对纤维状非织造材料的热传递已有广泛的研究,目的是为了优化产品设计和开发。Bhattacharyya开发了一个计算纤维状材料热传导的模型,该模型表明随着材料厚度与平均温度的增加,有效热导率增加[4]。Stark和 Fricke对 Bhattacharyya的模型进行了改进,引进了纤维取向的概念。考虑到固态和气态之间传导的耦合,他们得到了一个与实验结果吻合的模型。结果表明,有效热导率是温度、密度和空气压力的函数[9]。Lee和Cunnington开发了一个对高孔隙率纤维隔热材料辐射热传递的理论模型,并用石英纤维做了实验验证[10]。Mohammadi等计算了多层陶瓷和针刺玻璃纤维非织造材料的有效热导率。他们的统计分析表明,通过织物的面密度、厚度、孔隙率和使用温度能足够精确地预测有效热导率[11]。他们还计算了总热量的传导组成,分析并估算了样品的辐射热导率。计算结果表明,在结构中加入玻璃纤维增加了辐射传导,因为玻璃纤维比陶瓷的堆积密度更低,产生了更高的量子自由路径[1]。Wang等用点阵Boltzmann算法对纤维状材料的有效热导率做了数字模拟。他们的模型揭示了随纤维长度的增加,热导率增加,但在纤维长度足够长之后则热导率几乎保持不变[12]。
数字及解析的模型研究使人们对纤维状隔热材料的热传递有了比较深刻的理解,但是其中大部分研究结果尚不能用于实践,因为它们太复杂以至于使用非常困难。本文利用实验观察,得到表观热导率与絮片的比体积之间的线性关系,为选择具有成本效益的纤维状隔热材料提供有用的计算方法和途径,为产品设计和开发提供参考。
1 实验
1.1 测试方法和仪器
所有的热导率都使用Holometrix,Inc.,k-Matic(德国耐驰集团)热导率测定系统进行测定。k-Matic测量系统是一个在线监视的平板系统,假定边缘流动损失或干扰能够忽略。ASTM C518就是使用这一手段的[13]。k-Matic计算从一个设定温度[24℃(75℉)]的热表面到另一个设定温度[0℃(32℉)]的冷表面的热通量。样品室能容纳30 cm×30 cm(12 in×12 in)的样品,其厚度为7.6~3.8 cm(3~1.5 in)。热通量是通过冷板中间10 cm×10 cm(4 in×4 in)的面积来获得。热导率由仪器计算。

式中:Φ——热通量[Btu/(h·ft2)];
Δt,ΔT——分别为两个表面之间的距离和温度差[14]。
在每次测定之前,仪器调整到已知的标准,在每次测定之后校正仪器的漂移;测定时间根据样品的厚度和密度而定,较厚和密度较大的样品需要较长的时间才能建立起平衡。
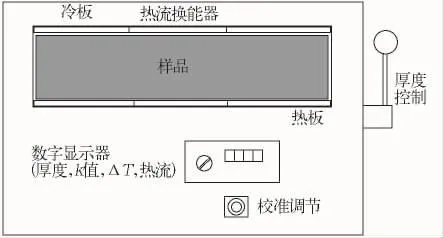
图1 热流测量装置 Holometrix K-Matic[14]
1.2 材料
所有测试的材料都是Auburn大学生产的气流成网热黏合非织造材料。黏合剂是CelBond纤维(3.3 dtex×5 cm的复合纤维),使用量为20%(质量分数)。主要纤维的选择范围很宽,包括卷曲的玻璃纤维 Miraflex(4.4 dtex×5 cm)、聚酯纤维(3.3 dtex×5 cm)、羽绒、鸡毛和氧化聚丙烯腈Panox(3.3 dtex×6.35 cm)。主要纤维以 80%(质量分数)的配比与黏合用纤维混合。通过铺网和黏合,或在装置上调节材料厚度不小于设定的最小值,来保证样品的密度差异。铝箔、聚乙烯膜由当地的商店采购。
2 结果和讨论
2.1 纤维状材料的保温性
由于实验的仪器不能区分传热的机理,前期做了一些实验以便区分和理解在纤维结构材料操作时热传递的机理[15-16]。这一工作是通过使用多层的各种薄膜和用框架分隔的细小空间(约0.635 cm)来实现的。材料包括透明的和黑色的聚乙烯膜、纺粘聚酯非织造材料和铝箔。测得的表观热导率k见表1。
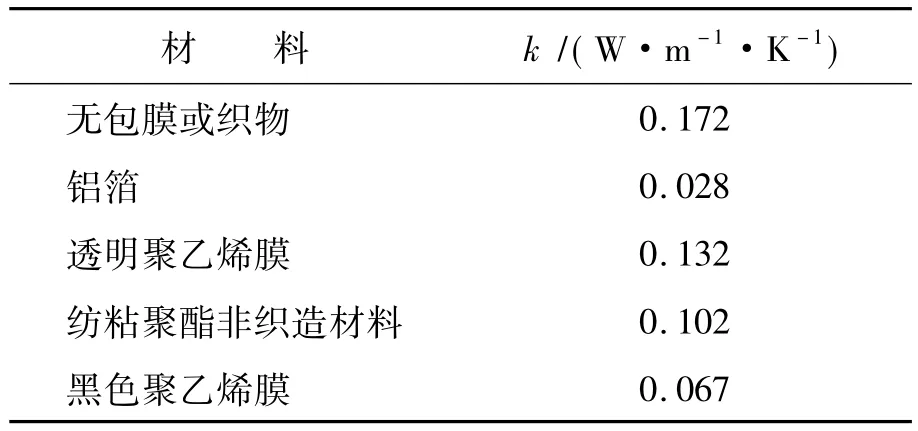
表1 不同材料的表观热导率k
在没有薄膜的情况下,包括对流和辐射传热在内,其表观热导率是0.172 W/(m·K)[1.196 Btu·in/(h·ft2·℉)]。对于铝箔,测得的热导率与静态空气中所测得的数值一样,说明在该系统中对流和辐射传热可以忽略。铝箔的高热传导性几乎对样品总的热传导性没有什么影响。如果把铝箔换成家用食品包装膜(透明聚乙烯膜),则材料的表观热导率为0.132 W/(m·K)[0.916 Btu·in/(h·ft2·℉)]。由于铝箔层防止对流,家用包装膜也有同样作用,导致表观热传导增加的原因必定是热辐射穿透了透明膜。对于纺粘聚酯非织造材料,表观热传导处于铝箔和透明膜之间,对辐射的透过率小于透明膜,在多孔材料内对流是很小的。对于黑色聚乙烯膜,辐射被吸收后重新发射,因此其表观热导率小于透明膜和纺粘聚酯非织造材料,但还是比铝箔要高,因为黑色聚乙烯膜发射能力要比铝箔高。由于静态空气的热传导不能被改变,纤维状隔热材料的主要作用是阻挡对流传递和减少电磁辐射。
2.2 理论方程的开发
隔热材料选择的标准永远是效率和成本的平衡。隔热效率经典的表达式是R值。R值是隔热材料的厚度与其本征热导率值的商。虽然对这一关系没有明确的描述,但是隔热材料的密度是有重要作用的。密度是单位体积材料的质量,而体积与厚度成正比。
图2是氧化PAN纤维隔热材料的热导率与密度的关系。图2中所示的曲线形状是典型的纤维状隔热材料密度与表观热导率的关系,在低密度区域[0.0~3.2 kg/m3(0.0~ 0.2 lb/ft3)]导热性特别的高,说明在这一区域隔热性能很差。原因是三种热传递方式都在起作用。因为密度很低,所以在纤维网内形成的空气单元足以形成对流[17]。此外,在低密度区域,材料中纤维所占的体积分数较低,不足以拦截辐射量子,阻挡热辐射[18-19]。在极端的低密度区域,固体纤维中的热传导不是非常重要,因为固体之间表面与表面的接触很少[6-7]。随着密度的增加,表观热导率的变化趋于平缓,接近静止空气的导热性。
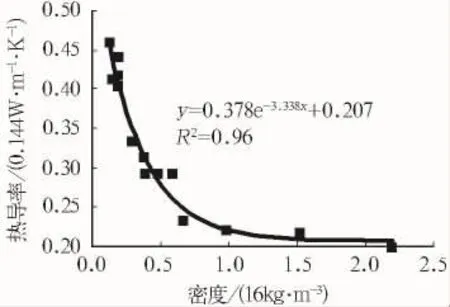
图2 氧化聚丙烯腈纤维的热导率与密度的关系曲线
当曲线延伸到另一个极端情况时,也就是材料密度非常高的时候,不论实验还是理论,都证明了曲线会以指数形式变化[20-21]。这是因为随着密度上升,材料几乎是固体状态。密度上升,平均自由路径减少,降低了传热中的热辐射[1-2]。另一方面,固体性的增加,传导传热增加[17,22]。当密度达到一个临界值,传导热量的增加超过了辐射热量的减少,导致表观热导性的上升[23-24]。
密度(ρ)的倒数称为比体积(Vsp),Vsp与给定重量材料所占的体积有关。图3使用了图2中相同的数据。当表观热导率对比体积作图时,得到一条直线。直线方程只对特定材料在特定区间有效。当密度很低时(比体积高),对流和辐射形式的热传递比较重要;当密度非常高的时候,热导率将接近固体纤维的热导率。幸运的是这一直线区域正好处于建筑隔热材料的密度范围。因为上述原因,在这个线性范围内,不论是对流还是通过固体的传导都是材料传热的重要方式,材料的隔热效率主要源自辐射传热的减少。

图3 氧化聚丙烯腈纤维的热导率与比体积的关系曲线
图3所示的线性方程表明,其y轴的截距K=0.2。这个值和单独的静止空气热导率很接近。重要的是:热导率与比体积关系是线性的,可以用线性方程(y=mx+c)表示:
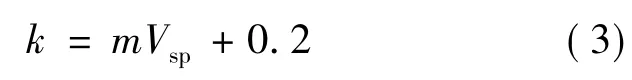
因为热阻R是用k来定义的,所以R也可以用上述方程定义:
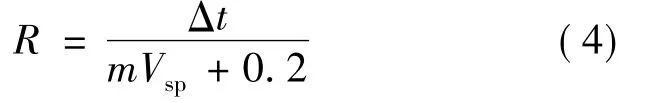
式中:Δt——厚度。
隔热材料的成本可能包括制造的成本,与使用的材料重量成比例。重量(W)是材料密度和体积(V)的乘积。材料的总成本是重量和单位重量成本的乘积。

设b=成本/单位重量,则:
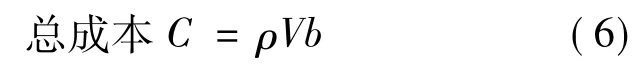

这里,体积V是面积(A)乘以厚度(Δt),则:
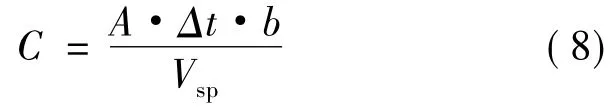
对单位面积归一化:

关联R和成本C:
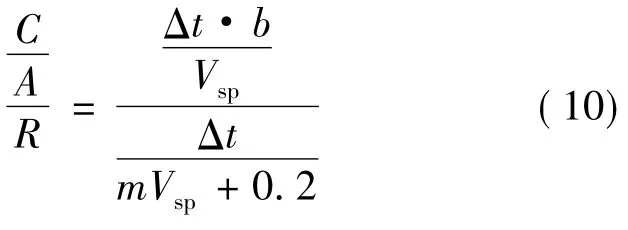

这一个方程是建立成本和效率关系的基础。斜率值m是单一材料的本征性能。单位重量的成本当然是一个要考虑的因素,但是它是一个外部的变量。
不同非织造材料的热导率单独测定,然后与比体积分别作图(图3和图4),由此就能回归出每种材料的斜率m。笔者认为斜率值是材料特有的,并可用于代表材料的传导行为。每个材料的斜率值合并到前面开发的方程中,用来评估隔热效率和成本。
由图3和图4可以明显看到氧化聚丙烯腈纤维与其他材料k值的区别。这一区别是前面评估所期待的。值得注意的是,不同材料之间(即聚酯纤维和羽毛、卷曲玻璃纤维和羽绒)k值的相似性。聚酯纤维和玻璃纤维之间的差别并不意外,因为它们分子结构是不同的。羽绒和鸡毛是有相同分子结构的材料,而在物理结构不同时纤维的直径会有很大差别。对于一个给定的重量或密度,占据相同的空间时,如果纤维的直径小,就需要更大量的纤维。因为纤维越细,其比表面积越大,辐射量子的自由路径就会变小[18,23,25]。
这一点可以通过使用相同分子结构,不同线密度的氧化聚丙烯腈纤维所做的实验得到进一步证明,其结果见图5。SP6和SP8分别代表直径是6和8 μm的纤维。虽然图5中所示的SP6和SP8之间的关系与预期相反,但是更适当的解释应当是没有明显差别,特别是在低比体积区间。
2.3 数据处理
测试样品热导率的目的不是确定哪种材料使用的成本效率最高,而是为建立模型提供一个宽阔的材料类型谱带。先对每种材料给定一个在目前市场上比较合理的单位重量的成本。

图4 一些测试样品的热导率
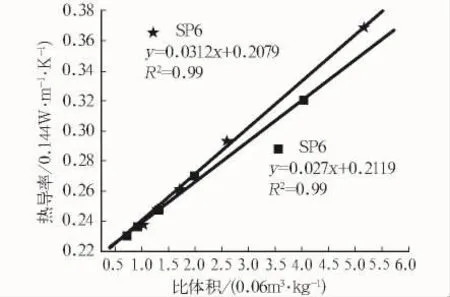
图5 氧化聚丙烯腈纤维直径对热导率的影响
为了计算一个纤维状结构材料的保温性,必须考虑四个变量:R值、厚度、体积密度以及k对比体积曲线的斜率。图6显示了厚度为8.89 cm(墙壁通用的厚度)时,斜率、密度和R值的关系。从图6可以看到,在低密度区选择隔热材料时,斜率值与R值有很大差别。例如,氧化聚丙烯腈纤维(斜率值0.037)在4 kg/m3(0.25 lb/ft3)密度下给出了R 值为1.76 m2·K/W(10 h·ft2·℉/Btu),而聚酯纤维(斜率值0.098)在相同密度下给出的R值几乎是氧化聚丙烯腈纤维的一半,为1.04 m2·K/W(5.9 h·ft2·℉/Btu)。从图6还可以看到,在体积密度增加后,R值的差别变得越来越小。在密度为96 kg/m3(6 lb/ft3)时,氧化聚丙烯腈纤维的R值为 2.99 m2·K/W(17 h·ft2·℉/Btu),聚酯纤维提供了几乎相同的值 2.85m2·K/W(16.2 h·ft2·℉/Btu)。随着密度增加[从0增加到96 kg/m3(6 lb/ft3)]R值也增加,更重要的原因是填充密度,而不是其化学成分。纤维的功能主要是通过创造出足够小的气穴,降低辐射量子的平均自由路程,分别来截断对流和减少辐射[1,4]。再有,在密度足够低的指定密度区域,当材料的种类变化时R值的差别很小,通过固体的热传导就少了。
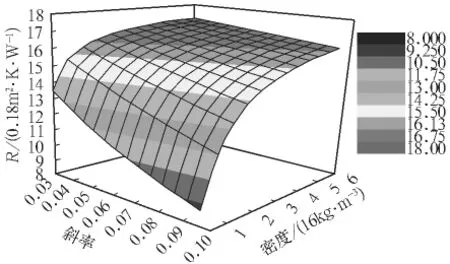
图6 厚度为8.89 cm材料的斜率、密度与R值的关系
虽然影响保温与成本之间的关系可以用图形生动地表示出来,但是在应用中使用表格更为方便,因为在图中很难看到细节。在方程(4)和(14)的帮助下,可以查阅包括单位面积成本和面密度的表格,来选择和优化隔热材料的成本(表2)。电子表格能实现对不同R值、密度、厚度和单位成本的计算。
材料单位重量的成本设定为:聚酯纤维0.75美元,卷曲的玻璃纤维0.25美元,氧化聚丙烯腈纤维为3美元,在厚度为8.89 cm,不同配置时,计算单位面积的成本和单位隔热材料的真正成本(单位面积成本×R)。表格可以进一步扩展,创造一个综合性的表格以利于选择具有成本效益的纤维状隔热材料。
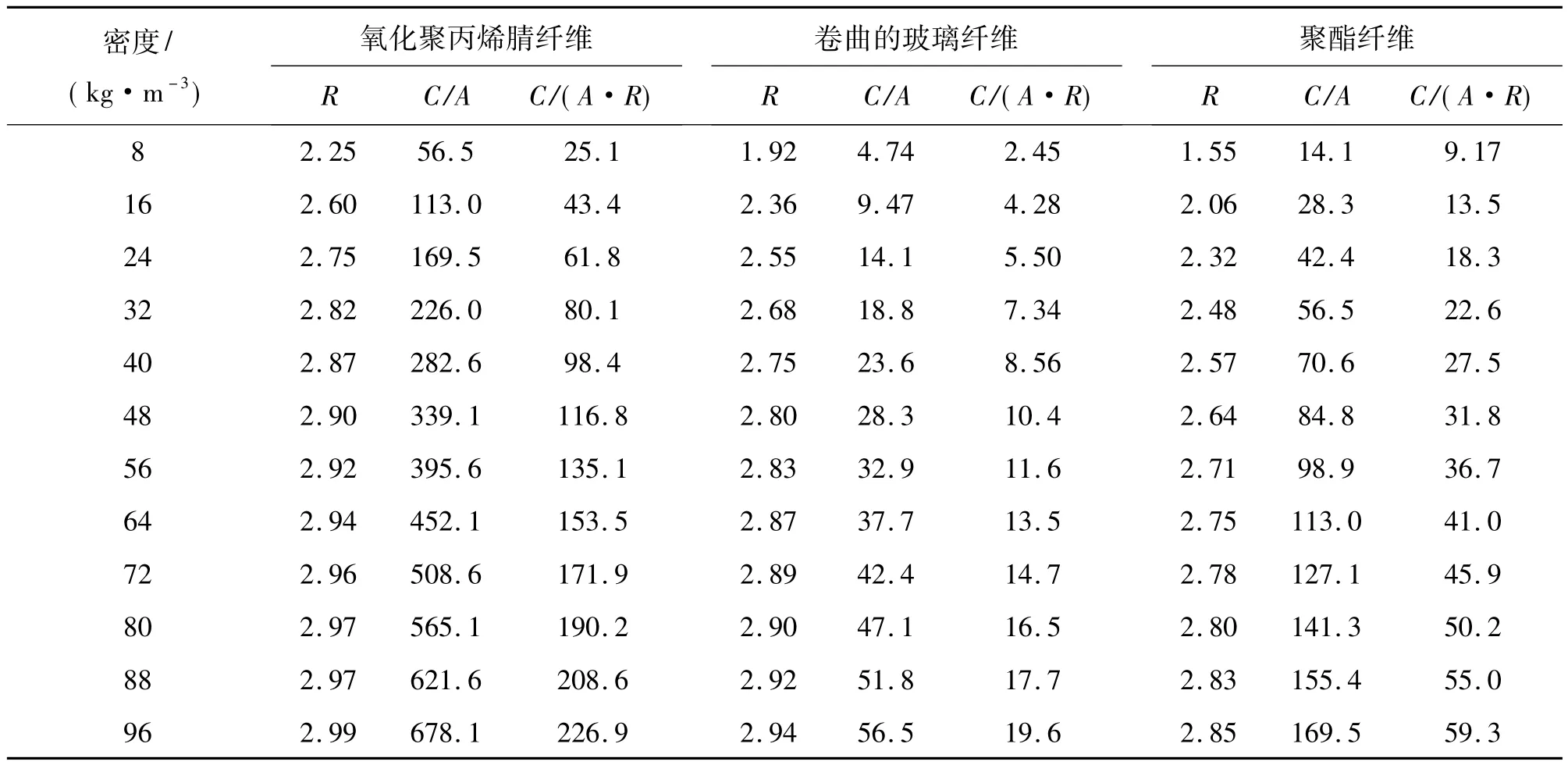
表2 厚度为8.89 cm时材料的成本计算
从表2得到的一个明显的结论是,选用任何一种玻璃纤维都比其他材料更经济。然而,氧化聚丙烯腈纤维在给定密度下,其R值最高。材料单位隔热成本之间的差别是随密度的增加而线性增加的,所以为了应用的目的,重量是关键,即使单位成本较高,选用氧化聚丙烯腈纤维也是合理的。另一方面,如图6所示,在高密度区域,材料类型对隔热作用的影响较小,这时不同种类材料的区别就显得重要了。这样,在没有体积和重量限制的情况下,选择低成本的玻璃纤维就更为合理。
3 结论
k对比体积作图所得的斜率似乎是纤维和织物成分的一个特性,该值可以用来计算k和不同密度时材料单位面积成本。换句话说,纤维和絮片的变量(不包括密度)能用k值对比体积曲线的斜率充分地表现出来。虽然这一点不能十分满意地满足理论家的要求,但是对实践中的计算很有帮助。如果知道了材料的密度和厚度,隔热材料的R值和面密度就能被计算出来。因为隔热材料是按照重量或者面积销售的,所以成本也可以计算出来。计算结果可以用图来表示,但是真正使用时,还是要用查表的方式。
假设一个材料的特定斜率系数可以测定,恰当地应用于优化成本似乎是有效的。考虑到所有材料,最低可用的密度20 kg/m3(此时对流能量可以忽略)是获得最大R值,从而获得期待的单位面积成本的起点。这一模型对多种纤维是有效的,并且比考察k值与密度提供了更多可应用的方法。
本研究中所用的测试方法是为了建筑隔热,所涉及的室内温度是人们生活舒适的温度,而室外温度是一般典型的温度。本模型在低密度区间0~96 kg/m3有效,对高密度和高环境温度没有进行过验证。
略)

