面向服务组合的密码服务调度智能优化研究

李建军，郁滨，陈武平

(1.信息工程大学 密码工程学院，河南 郑州 450004；2.信息保障技术重点实验室，北京 100072)

1 引言

随着我国信息化进程的不断推进，信息应用系统规模持续增大，单一的密码设备已无法满足需求，这已经成为制约电子政务和电子商务快速发展的瓶颈。大型的应用系统需要多种安全服务，对密码功能的需求也多种多样，但是与之配套的安全系统建设起步较晚，通用化、标准化程度不够。由信息化引发的信息安全问题不仅仅涉及国家的经济、金融和社会安全，同时也涉及到国防和政治安全。

20世纪90年代以来，Web服务技术得到了迅速发展。特别是随着面向服务架构（SOA）和云计算的蓬勃发展，Web服务组合的作用日益突显。这为安全系统建设提供了新的解决思路：借鉴Web服务技术，对各种提供密码功能的设备和系统等进行统一调度，使其可以为应用系统提供便捷、高效、安全的密码服务。由于密码服务的专业性更强，安全性和实效性要求更高，面对众多的密码服务，普通用户很难从中取舍，而对其进行组合的难度更大。因此如何构造密码服务的体系结构，并对众多密码服务进行合理的组合和调度，向用户提供更加透明、简洁和高效的密码服务是急需解决的问题。

本文针对密码服务的特点，提出了面向服务组合的密码服务体系结构，然后对其中的关键问题——密码服务调度问题进行分析，接着对混合蛙跳算法进行有针对性的改造，并加入变邻域搜索来提高局部搜索能力，使其可以对密码服务进行智能调度，最后对该算法进行了仿真和模拟实验。

2 面向组合的密码服务体系结构

密码服务是一种由安全协议、密码算法、密码基础设施、密码芯片等密码相关设备和系统提供的服务，包括加密、解密、数字签名、认证等安全服务以及密码资源管理服务等。密码服务作为一种特殊的服务，不但具有普通Web服务的特点，同时还具有准确性、保密性和时效性要求高、管理严格等特点。本文借鉴 SOA的结构，将其扩展为如图 1所示的密码服务体系结构。

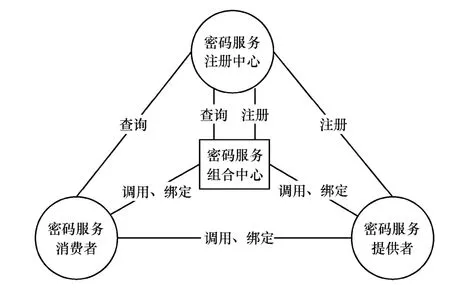
图1 密码服务体系结构

由于密码服务的特点，如果由密码服务消费者自身对密码服务进行组合和编排，无法保证其准确性和保密性，同时对服务质量也难以控制。因此在密码服务的体系结构中建立了一个密码服务组合中心，由该中心首先对密码服务注册中心的服务进行分类和抽象，然后由专业人员根据各种密码需求对密码服务提供者提供的服务进行组合和编排后对外发布。当这些组合服务被请求时，密码服务组合中心根据业务流程对密码服务提供者提供的服务进行动态调度。密码服务组合中心对业务流程的编排由专业人员进行，并经过形式化检测，因此可以很好地保证这些流程的正确性。另一方面在执行过程中密码服务组合中心可以根据密码服务提供者提供服务的状态对其进行动态调度，可以更好地保证服务质量。

3 密码服务调度问题

密码服务组合中心对各种密码服务进行组合，然后向用户提供多种多样的密码服务是种非常有效的手段。但是当大量的组合服务被调度时，密码服务组合中心需要针对用户的需求，对众多的密码服务进行有效调度，以保证服务质量。

目前针对密码服务调度的研究还很少，而调度问题的研究大多是针对网格环境下的服务调度[1]和制造工业中的作业车间调度问题[2,3]。其中，网格下服务调度研究对象一般分为2类[4]：一是作业级调度（job scheduling），二是工作流调度（workflow scheduling）。密码服务调度与研究对象是相互独立的，服务请求集合的作业调度差别很大；工作流调度虽然对密码服务调度有一定的借鉴作用，但是密码服务调度是基于 SOA的，而工作流调度是基于网格的，其调度方式差别很大。而作业车间调度中的柔性作业车间调度问题与密码服务调度相似，但是密码服务调度存在多种组合方案，结构更加灵活，调度难度更大。柔性作业车间调度中存在机器选择和工序排序2个子问题，而密码调度问题中存在组合方案选择、服务提供者选择和服务排序3个子问题。

对密码服务组合来说，每个服务组合有若干种组合方案，每个组合方案由若干种密码服务以特定顺序组合构成，其中，每种服务可以从若干个提供者中选择。因此可以表示为n个服务组合在m个提供者上加工。因此设M={Mk}(1≤k≤m)，C={Ci}(1≤i≤n)，每个服务组合所包含的组合方案为Pi,d(1≤d≤ui)，其中，ui为服务组合i包括的组合方案数量。每种组合方案中所包含的服务为Si,j(1≤j≤ni,d)，其中，Sij表示服务组合i的第j个服务，ni,d表示服务组合i的组合方案d所需要的服务数量。每个服务Si,j必须在候选提供者Mi,j,d⊆M中的一个提供者Mk上加工，其中，每个候选提供者对应一个加工时间Pi,j,d,k。Fi,j和Ti,j分别表示服务Si,j的开始时间和结束时间。Fmd,k,r为服务Si,j在组合方案d中以优先级r在提供者k上运行。qk为在提供者k上运行的服务数量。L为一个足够大的数。同时假设：每个服务组合和提供者在0时刻都可以被选择；每个提供者一次只能提供一个服务；每个服务Si,,j完成前不能停止。

4 改进的混合离散蛙跳算法

混合蛙跳算法是由Eusuff和Lansey[5]于2000年提出的一种全新群体智能进化算法，具有良好的灵活性和通用性等特点，在诸多领域都得到了广泛应用[6～8]。文献[9]在蛙群内引入吸引排除机制，有效地避免了算法的早熟收敛；文献[10]通过加入幂律极值动力学优化，提高了算法的寻优能力；文献[11]在子群内部搜索时加入过去的经验；文献[12]采用离散度和适应度来自适应地调节数列公比取值，以提高算法的收敛速度和精度。

为了利用混合蛙跳算法进行密码服务调度的优化，首先针对密码服务调度的特点，对其编码、解码进行设计。然后结合遗传算法的交叉操作对混合蛙跳算法中的矢量更新方法进行改造。最后为了克服传统混合蛙跳算法容易落入局部最优的缺点，并提高搜索的精度和速度，在传统混合蛙跳算法的基础上，利用变邻域算法对组内最优青蛙进行局部搜索。

4.1 编码

针对密码服务调度的3个子问题，本文对青蛙采用分段编码，1)确定组合方案的选择；2)确定每个服务所选择的提供者；3)确定每个服务的调度顺序。

1) 组合方案选择编码

该部分编码比较简单，每比特基因都是一个整数，用来表示确定该可行解中每个服务组合所选择的组合方案。该部分编码的总长度与服务组合的总个数相同。如图2中的组合方案选择编码所示，其中，服务组合C1选择第二套组合方案，其他服务组合全部选择第一套组合方案。

2) 提供者选择编码

该部分每个青蛙中每比特基因也用整数表示，依次为每个服务组合所确定的那套组合方案中每个服务所选择的提供者编号。为了后续的计算方便，这里不采用对应的提供者下标，而是每个服务候选提供者中的排序。以表1所示的实例为例，如图 2中服务提供者选择编码所示服务组合C1选择组合方案2，其中，S11对应可选择的服务者集中有4台，该青蛙选择第1台机器加工；而S12对应可选择的服务者集中有3台，该青蛙选择第4台机器加工，以此类推。同时为了保证每个青蛙编码的总长度相同，该部分编码中每个服务组合对应的服务数量数以所有选择方案中含有服务数量最多的为准。例如表1中的服务组合C3共有2个组合方案，其中，组合方案1有2个服务，组合方案2有3个服务。在图 2的提供者选择编码中C3对应的基因数量就是3个，虽然其在组合方案选择编码中选择的是组合方案1，但是该部分还是有3个提供者选择基因。

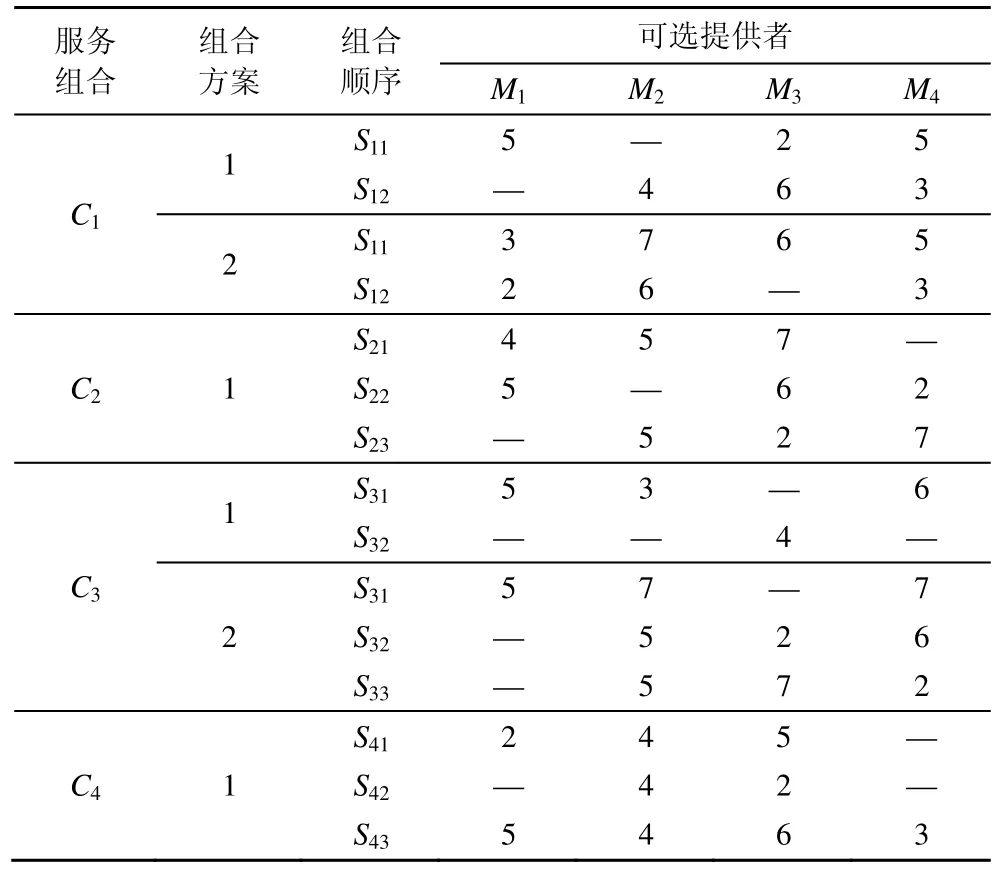
表1 密码服务调度问题实例

3) 服务排序编码

图2 青蛙编码

该部分的编码以同一服务组合的所有服务采用相同的数字来表示，而同一个服务则根据其在青蛙中出现的先后次序来决定其在服务组合中的排序。如图2所示第一个3对应的是服务组合3的第一个服务，第一个2对应的是服务组合2的第一个服务，第二个3对应的是服务组合3的第二个服务，以此类推。其中，由于服务组合3选择的组合方案是 1，这里虽然只有 2个服务，但是为了与提供者选择编码对应，该部分编码里面仍然有3个3。而第3个3对应的加工时间为0。这样既可以保证青蛙的编码总长度一致，又不会改变该青蛙的总加工时间。

4.2 解码

解码是将青蛙转化为一个调度解。本文采用的是一种可插入的解码方式，该方式可以把每个服务放在最佳可行位置调度。首先根据组合方案编码确定每个服务组合所选择的组合方案，然后根据提供者选择编码部分确定每个服务对应的提供者。设任意一个服务Sij的加工时间为t，在服务者m上执行。它的前一个服务的结束时间为TSij-1，如果Sij为服务组合的第一个服务，则TSij-1=0。而服务者m上已加工的服务之间可能存在时间间隔，假设有k个时间间隔[TBk,TEk]，因此如果max(TSij-1,TBk)+t≤TEk，那么该服务Sij可以插入到这个时间间隔来加工，否则就在提供者m后继续加工。以此方法可以把每个服务都安排在其最佳可行的位置上。图2的青蛙解码后的甘特图如图3所示。其中，S12则可以插入到S22之前。

图3 青蛙解码后的甘特图

4.3 矢量更新方法

在传统 SFLA中，青蛙的更新公式为Pwnew=Pw+rand()*(Pb-Pw)，其中，rand()为0～1的随机数，Pw为组内最差青蛙，Pwnew为更新后得到的新青蛙。当与组内最优青蛙进行更新时，Pb为组内最优青蛙；当与全局最优青蛙进行更新时，Pb为全局最优青蛙。

本文根据SFLA的特点，利用两两交叉来更新青蛙。当与组内最优青蛙进行更新时，利用组内最优青蛙和最差青蛙进行交叉，得到新青蛙；当与全局最优青蛙进行更新时，利用全局最优青蛙和最差青蛙进行交叉，得到新青蛙。由于青蛙的编码中包括3部分，需要分别进行交叉。其中，服务排序部分在POX操作[13]的基础上进行改造，如图4所示。首先将所有服务随机分成2个集合J1和J2。然后父代P1和P2分别保留属于J1和J2的服务到子代F1、D1和F2、D2，保持位置不变。最后把P2中属于J1的复制到D1、P2中，属于J2的复制到F1、P1中，属于J1的复制到F2、P1中，属于J2的复制到D2，保持顺序不变。

图4 服务排序编码的交叉操作

组合方案选择部分的交叉操作和服务者选择部分的交叉操作相同，如图5所示。首先从编码的所有位置中随机选择r个位置。然后把P1中属于这r个位置的提供者复制给D2，将剩余位置的提供者复制给D1，最后把P2中属于这r个位置的提供者复制给D1，将剩余位置的提供者复制给D2。该交叉操作没有改变位置，只交换同一服务对应的提供者（和同一个服务组合对应的组合方案），因此产生的子代必为可行解。

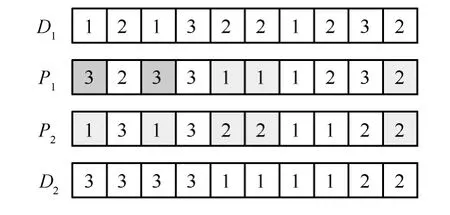
图5 组合方案选择编码和提供者选择编码的交叉操作

通过服务排序编码交叉共产生4个服务子代，通过提供者选择编码交叉共产生2个提供者子代，通过组合方案选择编码交叉共产生2个组合方案子代，共可以组合成16个青蛙，从这16个青蛙中选出最优青蛙作为交叉后产生的新青蛙。

4.4 算法流程

在传统的混合蛙跳算法中，只对每组蛙群中的最差青蛙进行更新，因此只有在重新产生的青蛙的适应度优于最优青蛙时，最优青蛙才会更新，因此其收敛速度较慢且易于早熟。本文在传统混合蛙跳算法的基础上，增加了蛙群中最优青蛙的邻域搜索策略，并引入了变异操作。改进混合蛙跳算法的具体步骤如下。

Step1初始化随机产生F只青蛙。

Step2评价每个青蛙的个体适应值。

Step3根据每个青蛙的适应值，由优至劣进行排序。

Step4把排序后的青蛙分成m组，每组n只青蛙。其中，第一只青蛙分到第一组，第二只分到第一组，…，第n只青蛙分到第一组，第n+1个青蛙分到第二组，以此类推直到所有青蛙分配完毕。

Step5对每组青蛙进行t次局部搜索。

a对组内最优青蛙进行变邻域搜索。

b对利用组内最优青蛙对组内最差青蛙进行更新。如果无法更新，则利用全局最优青蛙对组内最差青蛙进行更新。如果仍然无法更新，则随机生成一个新青蛙代替组内最差青蛙。

Step6如果满足终止条件，则停止搜索，输出全局最优青蛙，反之则转到Step3。

4.5 邻域搜索策略

本文的邻域搜索策略包括6种邻域构造方法。

1) 对提供者选择编码和组合方案选择编码部分保持不变，只改变服务编码部分。具体方法为：对包含2个及2个以上的关键块中头2个或后2个服务进行交换，但是第一个关键块的前 2个服务和最后一个关键块的后 2个服务不进行交换。如果交换的2个服务属于同一个服务组合则无需交换。该交换可以保证交换后的编码仍然会有可行解[14]。

2) 对服务排序编码部分和组合方案选择编码部分保持不变，只改变提供者编码部分。具体方法为：随机选择一个关键路径上的服务，如果该服务的可选提供者集合中只存在一台机器，则重新选择服务。如果存在2个提供者，则选择另外一个提供者。如果存在 3台提供者，则随机产生一个 0～1的随机数，如果该随机数大于 0.8，则选择执行时间短的提供者，反之则选择执行时间长的提供者。

3) 对提供者选择编码部分和组合方案选择编码部分保持不变，只改变服务排序编码部分。具体方法为：随机选择一个提供者，对该提供者上执行的服务进行重新排序。新排序遵循的约束条件为最早开工时间小的优先加工，如果最早开工时间相同，则选择在服务编码中位置靠前的优先加工。

4) 对服务排序编码部分和组合方案选择编码部分保持不变，只改变服务提供者编码部分。具体方法为：提供者编码中随机选择r个位置，然后选择这r个位置各自对应的可选提供者集合中加工时间最短的机器作为新的加工机器。

5) 对服务提供者编码部分和组合方案选择编码部分保持不变，只改变服务排序编码部分。具体方法为：随机产生一个0～1的随机数。如果该随机数大于0.5，则服务编码中随机选择2个位置，将这2个位置之间的服务倒序排列。反之则随机选择2个位置，让一个位置的服务插入到另一个之前。

6) 对服务提供者编码部分和服务排序编码部分保持不变，只改变组合方案选择编码部分。具体方法为：组合方案选择编码中随机选择r个位置，然后选择这r个位置各自对应的组合方案可选集中随机选择另外一个方案。

利用上述6种邻域、变邻域搜索伪码如图6所示。上节Step5中的a中即是利用该算法对组内最优青蛙进行深度搜索。

图6 变邻域搜索伪码

5 对比实验与结果分析

为了更好地验证本文提出算法的有效性，本文搭建密码服务组合实验环境，在密码服务组合中心原型系统中测试本文提出方案的有效性。

该实验环境如图7所示，其中，服务提供者由5台CPU为Intel Xeon E5540，8 GB内存，500 GB硬盘的密码服务器担当，本文开发的密码服务中心原型系统部署在CPU为Intel Xeon E7430，32 GB内存的联想服务器上，用户端为25台主频2.8 GHz，内存为1 GMB的PC。为了更加真实地模拟实际网络环境，每台密码服务器上部署5个不同的密码服务，并通过5个不同的端口同时对外发布。每台PC机上可以并行运行 20个服务请求程序，这样最多可以模拟500个用户。

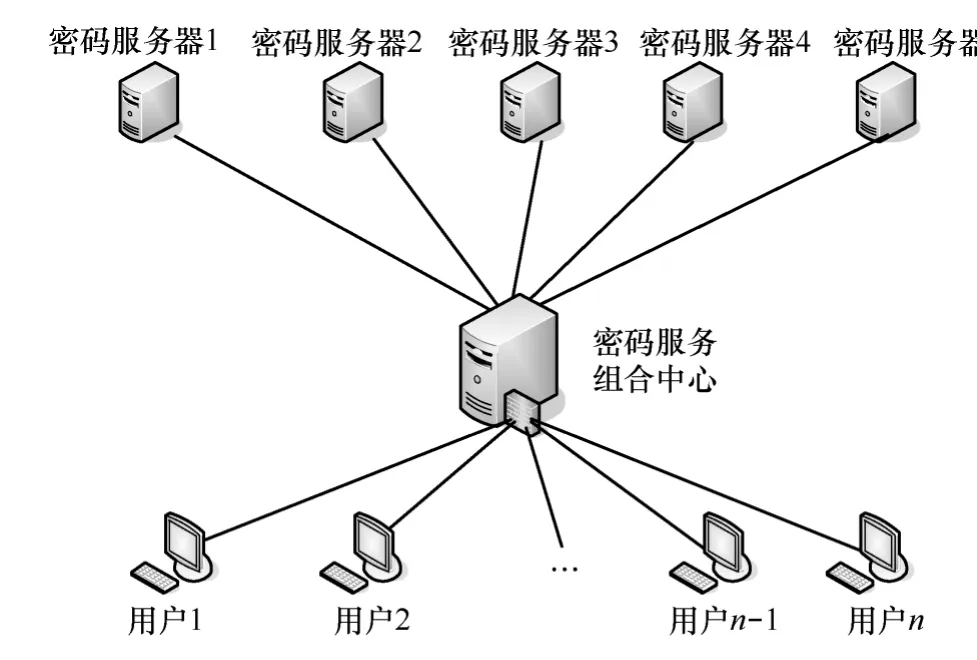
图7 密码服务组合实验环境

实验中共发布25个（15种）服务，共组合成50种密码服务组合，其中，组合方案最多的为5种，最少的为 2种。用户端的用户请求数从 100增至500，每个服务请求程序从50种密码服务组合中随机选择一种进行请求，密码服务组合中心分别采用本文改进的混合离散蛙跳算法和随机选择2种调度策略，分别记录用户中最长完成时间和5台密码服务器的负载率（一台服务器执行服务的总时间/用户最长完成时间）。为了更加客观地模拟实际环境，用户端同时发出请求，2种调度策略对比时其请求的密码服务组合种类和数量完全相同，分别独立运行20次后取平均值，实验结果如图8～图10所示。

图8 最大完成时间对比结果

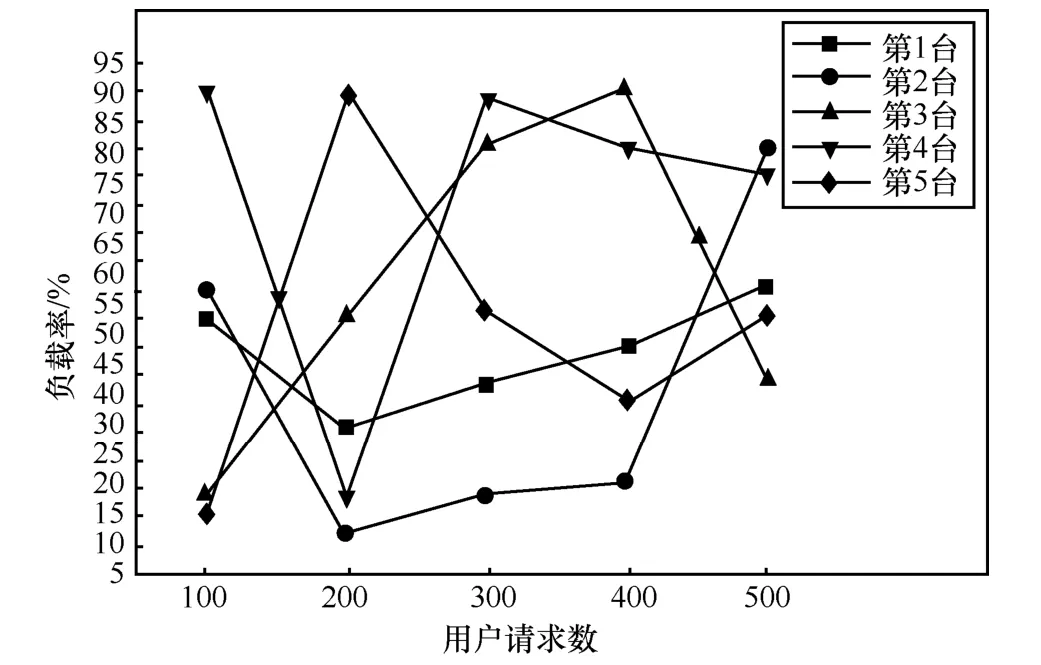
图9 随机选择时，5台服务器负载率

图10 本文算法时，5台服务器负载率

从图8可以看出随着服务请求数的增加，用户最大完成时间都在增大，但是随机选择时增加特别明显，且与本文算法的差距越来越大。从图9可以看出在随机选择时，尽管进行了 20次独立实验，但是 5台服务器无论在用户请求数多或少的情况下，其负载率差别很大，在同一用户请求数下，有的服务器负载率高达90%以上，而有的只有20%左右。从图10可以看出本文算法可以保证5台服务器的负载率相对平衡，无论在哪个用户请求数下都保持相对稳定。因此本文算法在解决密码服务调度问题上无论是最大加工时间还是负载均衡均优于随机选择。

6 结束语

目前，针对密码服务体系结构和调度问题的研究尚未出现，本文首次进行了该方面的研究。由于密码服务自身的特性，其必然与其他Web服务存在着巨大的差别。本文提出的面向组合的密码服务体系结构为大规模网络条件下的信息系统安全保障提供了新的解决方案。针对密码服务调度的智能优化算法对传统混合蛙跳算法的编码、解码、个体更新方案等方面进行了有针对性的设计。特别是在传统混合蛙跳算法对全局搜索和局部搜索进行有效平衡的基础上，引入多种邻域结构，使得混合离散蛙跳算法在解决密码服务调度问题更加高效和稳定。本文的研究对密码基础设施建设有很强的指导意义。

[1] 谭雅丽, 于炯, 邓定兰等.基于多维 QoS 约束的网格任务调度算法[J].计算机工程, 2010, 36(12):75-77.TAN Y L, YU J, DENG D L,et al.Grid task scheduling algorithm based on multi-dimensional quality of service constraints[J].Computer Engineering,2010,36(12):75-77.

[2] CHEN J C, CHEN K H, WU J J,et al.A study of the flexible job shop scheduling problem with parallel machines and reentrant process[J].Intelligent Journal of Advance Manufacturing Technology, 2008,39(3-4):344-354.

[3] ZHANG G H, SHAO G H, LI P G,et al.An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem[J].Computer & Industrial Engineering, 2009, 56:1309-1318.

[4] 张伟哲, 方滨兴, 胡铭曾等.基于信任 QoS增强的网格服务调度算法[J].计算机学报, 2006, 29(7):1157-1166.ZHANG W Z, FANG B X, HU M Z,et al.A trust-QoS enhanced grid service scheduling[J].Chinese Journal of Computers, 2006, 29(7):1157-1166.

[5] EUSUFF M M, LANSEY K E.Optimization of water distribution network design using the shuffled frog leaping algorithm[J].Water Resour Plan Manage, 2003, 129(3):210-225.

[6] NIKNAM T, FARSANI E A, NAYERIPOUR M,et al.A new tribe modified shuffled frog leaping algorithm for multi-objective distribution feeder reconfiguration considering distributed generator units[J].European Transactions on Electrical Power, 2012, 22(3):308-333.

[7] ZHANG X D, ZHANG Y F, SHI Y H.Power control algorithm in cognitive radio system based on modified shuffled frog leaping algorithm[J].International Journal of Electronics and Communications,2012, 66(6):448-454.

[8] SELVAKUMAR K, VENKATESAN T, SANAVULLAH M Y.Price based unit commitment problem solution using shuffled frog leaping algorithm[A].IEEE International Conference on Advances in Engineering, Science and Management[C].2012.794-799.

[9] 王介生, 高宪文.基于改进混合蛙跳算法的电渣重熔过程多变量PID控制器设计[J].控制与决策, 2011, 26(11):1731-1734.WANG J S,GAO X W.Design of multivariable PID controller of electroslag remelting process based on improved shuffled frog leaping algorithm[J].Control and Decision.2011, 26(11):1731-1734.

[10] 骆剑平, 李霞, 陈泯融.基于改进混合蛙跳算法的 CVRP求解[J].电子与信息学报,2011,33(2):429-434.LUO J P, LI X, CHEN M R.Improved shuffled frog leaping algorithm for solving CVRP[J].Journal of Electronics & Information Technology, 2011, 33(2):429-434.

[11] 郑仕链, 楼才义, 杨小牛.基于改进混合蛙跳算法的认知无线电协作频谱感知[J].物理学报, 2010, 59(5):3611-3616.ZHENG S L,LOU C Y, YANG X N.Cooperative spectrum sensing for cognitive radios based on a modified shuffled frog leaping algorithm[J].Acta Physica Sinica, 2010, 59(5):3611-3616.

[12] 肖莹莹, 柴旭东, 李伯虎等.混合蛙跳算法的收敛性分析及其改进[J].华中科技大学学报(自然科学版), 2012, 40(7):15-18.XIAO Y Y, CHAI X D, LI B H,et al.Convergence analysis of shuffled frog leaping algorithm and its modified algorithm[J].Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(7):15-18.

[13] 张超勇, 饶运清, 李培根等.柔性作业车间调度问题的两级遗传算法[J].机械工程学报, 2007, 43(4):119-124.ZHANG C Y, RAO Y Q, LI P G,et al.Bilevel genetic algorithm for the flexible job-shop scheduling problem[J].Chinese Journal of Mechanical Engineering, 2007, 43(4):119-124.

[14] NOWICKI E, SMUTNICKI C.A fast taboo search algorithm for the job shop problem[J].Management Science, 1996, 42(6):797-813.