Eurocode3 1-6与 DIN18800-4在风电机组塔架屈曲分析中的对比研究
王露
(北京鉴衡认证中心,北京 100013)
Eurocode3 1-6与 DIN18800-4在风电机组塔架屈曲分析中的对比研究
王露
(北京鉴衡认证中心,北京 100013)
目前,针对风电机组塔架的屈曲分析一般采用工程算法,欧洲标准Eurocode3 1-6与德国标准DIN18800-4是两种十分常用的工程计算方法,两者对于塔架设计中的抗屈曲问题都有很强的指导意义,同时在计算思想上也有异曲同工之处。本文针对两部标准中与风电机组塔架屈曲设计相关的部分进行了比较与分析,为相关研究提供了一定的参考。
塔架; 屈曲; 工程算法; 算法比较
0 引言
风电机组塔架多为圆锥薄壁筒型结构,它的主要破坏形式之一是整体或局部的屈曲失稳破坏[1]。目前多采用Eurocode3 1-6与DIN18800-4两部标准对塔架稳定性进行分析。
在Eurocode3 1-6和DIN18800-4中,有很多对应的概念,在计算过程中有等同的作用,在理论上有相同的物理意义和理论基础。以轴向应力分析时所用到的概念为例,对等概念如表1所示。
在环向应力和切应力分析中,这些基本概念也是对等的。这些定义与概念是整个标准的基础,可见Eurocode3 1-6 与DIN18800-4两部标准整体上有非常类似的框架结构和理论基础,从而在应用时,计算过程的思路也是大同小异的。图1、图2分别给出这两部标准的计算过程流程图,下面将针对各个计算要点进行对比分析。
1 计算要点对比分析
1.1 理想屈曲应力(或临界屈曲应力)
理想屈曲应力(在Eurocode3 1-6中称作“弹性临界屈曲应力”,下文中都使用“理想屈曲应力”这一概念)在两部标准中的计算结果差别主要来自于关系系数C,对于同一结构理想屈曲应力与关系系数成正比关系。

同样对“短筒”(ω≤1.7)壳体的计算公式进行比较,可以发现对于同一“短筒”壳体,当0.35<ω≤1.7时DIN18800-4的计算方法将得到较大的轴向理想屈曲应力。而当 时Eurocode3 1-6方法下计算所得轴向理想屈曲应力较大,但“短筒”在风电机组塔架中很少出现。
对于环向理想屈曲应力和理想屈曲切应力计算中的关系系数,用同样的方法进行比较,两部标准中的比较结果如表2所示。
风电机组塔架的焊接段大部分属于“长筒”或“中长筒”:对于“长筒”焊接段,其三种理想屈曲应力的计算结果相同;对于“中长筒”焊接段,DIN18800-4计算所得的三种理想屈曲应力均大于Eurocode3 1-6。但实际屈曲应力(Eurocode3 1-6中定义为“特征屈曲应力”)和极限屈曲应力(Eurocode3 1-6中定义为“设计屈曲应力”)哪种方法所得结果更大,需结合屈曲缩减系数的计算公式和安全系数的取值来确定。
1.2 制造缺陷

图1 DIN18800-4结构屈曲计算流程图
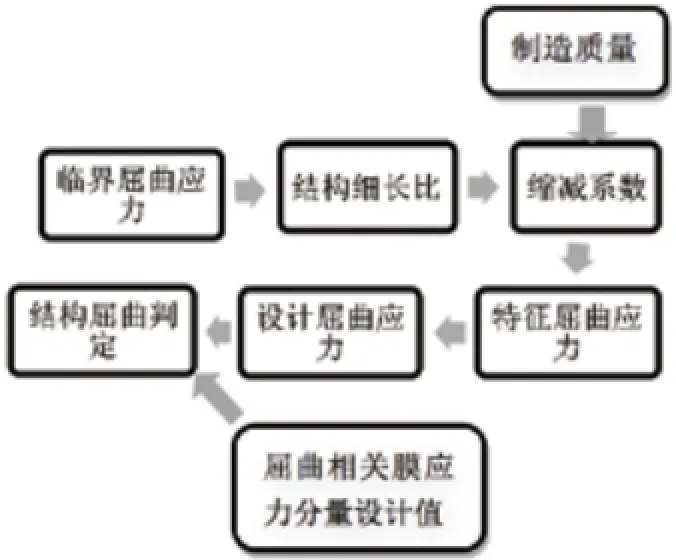
图2 Eurocode3 1-6结构屈曲计算流程图

表1 Eurocode3 1-6与DIN18800-4轴向应力部分中的对等概念

表2 DIN18800-4和Eurocode3 1-6中理想屈曲应力计算值对比
塔架的制造缺陷对于结构的承载能力有着十分重要的影响,在两部标准中规定了三种相同的缺陷检验类型,分别是凹陷、不圆度、偶然偏心度,在Eurocode3 1-6中还简单对“接触面平整度”这项缺陷做出了规定。两部标准对于不同缺陷类型的公差和缺陷测量方法都给出了明确的规定。
在Eurocode3 1-6中对应于不同的制造公差质量等级(分为A、B、C三级)给出了大小不同的最大缺陷度允许值,当塔筒制造质量处于较低的质量等级时,会导致计算过程产生较小的屈曲缩减系数,也就是说,同样尺寸、外形的塔架,制造质量等级偏低的,只能承受较小的屈曲载荷。在DIN18800-4中,没有进行公差质量等级的分类,而是直接给出了最大缺陷度允许值。他们的差别以“不圆度”这种缺陷类型举例:
在Eurocode3 1-6中,设定参数:
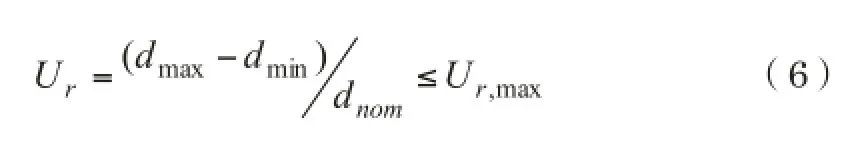
dmax是测量到的最大的内经,dmin是测量到的最小的内径,dnom是公称内径。对应于不同质量等级的不圆度公差值见表3。
DIN18800-4中设定参数:

d的单位为mm,max d是测量到的最大内经,min d是测量到的最小内径。在制造偏差不是很大的情况下,Ur和U的计算结果差别是较小的,但DIN18800-4中要求对于所有内径d≥1250mm的情况zulU=0.005,这个质量要求比Eurocode3 1-6中的A级更高。考虑风电机组塔筒直径通常大于1250mm,可见对于风电机组塔筒圆度DIN18800-4提出了更高的要求。对于“凹陷”而言,考虑到风电机组塔架的实际情况,DIN18800-4中提供的缺陷允许值基本等同于Eurocode3 1-6中的B级公差。而对于“偶然偏心度”,DIN18800-4所要求的制造质量则通常在Eurocode3 1-6的A、B等级之间。
对于缺陷的测量方法,Eurocode3 1-6中的要求是比较复杂的,特别是对于凹陷的测量,凹陷测量长度与应力种类和是否穿过焊缝都有直接关系。DIN18800-4中的要求则略为简便、明确,与应力种类和是否穿过焊缝没有直接关系。综合对比后可发现,对于制造缺陷,Eurocode3 1-6和DIN18800-4两部标准总体的质量要求哪一种方法更高,还需要视具体缺陷类型和结构尺寸而定。
1.3 屈曲缩减系数
屈曲缩减系数考虑了结构的缺陷程度和材料的非完全弹性作用,通过屈曲缩减系数修正材料的屈服强度,从而得出实际结构所能承受的最大屈曲应力。计算屈曲缩减系数的重要参数是无量纲细长比(在Eurocode3 1-6中用细长比的平方与理想屈曲应力成反比例关系。
在Eurocode3 1-6中屈曲缩减系数χ的计算过程是比较复杂的,对应三种应力类型计算过程各不相同,涉及到诸多变量。在DIN18800-4中,屈曲缩减系数分为一般缺陷敏感度x1和高缺陷敏感度x2两组取值,从直观上看,它只与无量纲细长比有关,是一种简化的计算方法。下面按照三种应力类型分类进行比较。
在计算轴向的屈曲缩减系数时,DIN18800-4中取x2的一组公式,Eurocode3 1-6中的不确定因子较多与DIN18800-4不易比较,从往常的计算经验来看,对于“长筒”和“中长筒”当质量等级取A或B级时,同一结构Eurocode3 1-6计算所得的轴向屈曲缩减系数往往大于DIN18800-4。
计算环向和切应力的屈曲缩减系数时,DIN18800-4中取x1的一组公式,可将Eurocode3 1-6的计算过程按照不同的质量等级整理成以下公式:
当取质量等级A时:


表3 Eurocode3 1-6中不圆度公差系数Ur.max推荐值

图3是DIN18800-4和 Eurocode3 1-6两组计算公式的比较图,其中从上到下三条蓝色曲线对应Eurocode3 1-6中质量等级分别为A、B、C级时的环向和切应力的屈曲缩减系数曲线,红色曲线是DIN18800-4中屈曲缩减系数x1的曲线。
可见无量纲细长比相同的情况下,DIN18800-4中的屈曲缩减系数计算结果基本与Eurocode3 1-6中取B级时的计算结果相同,后者稍大。综合分析理想屈曲应力、无量纲细长比、并结合经验可将屈曲缩减系数的比较结果总结为表4。
1.4 其他对比分析结果
以上各节对两部标准的计算方法中引起差别的重要部分进行了分析,对于最后的屈曲安全判定,还有一些影响因子:安全系数是影响极限屈曲应力(Eurocode3 1-6中定义为“设计屈曲应力”)值的一个重要参数,Eurocode3 1-6中安全系数的推荐值为1.1;在DIN18800-4中,根据不同的缺陷敏感程度,安全系数的取值为1.1(环向应力和切应力)或大于1.1(轴向应力)。另外,两部标准中每种应力的单独判定方法是相同的,三种应力综合判定方式从公式来说,除各项指数有所不同外,Eurocode3 1-6还比DIN18800-4多出一项,两者计算结果数值差距的大小需视具体情况而定。
2 圆锥壳
圆锥型壳体结构的屈曲计算采用了转化的思想,等效圆柱长度和等效圆柱半径的计算公式在两部标准中均由应力类型确定。当计算轴向屈曲应力时,两部标准的等效长度及半径的转化公式是一致的,区别主要在于计算环向应力和切应力时的等效方法:Eurocode3 1-6中首先提供了一般情况下等效长度和等效半径的计算方法,然后又针对“壳体环向受均匀外压引起环向应力”和“壳体受均匀扭转引起切应力”这两种受载的特殊情况给出了等效长度和等效半径的经济算法,经济算法所得设计屈曲应力较大。当受载不满足以上两种特殊条件时,Eurocode3 1-6 D4.3.2和D4.3.3中指出,计算屈曲相关膜应力设计值时,可以通过包络实际载荷的方法,将不均匀的载荷转化为均匀的载荷形式;DIN18800-4在计算这两种极限屈曲应力时只给出了一种方法,它实际上与Eurocode3 1-6中的经济算法是等效的。
以圆锥型壳体结构环向屈曲应力和屈曲相关膜应力设计值(DIN18800-4中定义为“有效膜应力”)的计算方法举例,Eurocode3 1-6中指出,当壳体环向受均匀外压引起环向应力时,等效圆柱筒长度 的经济算法是取下面两个公式的较小值,并对应等效半径 的不同公式。
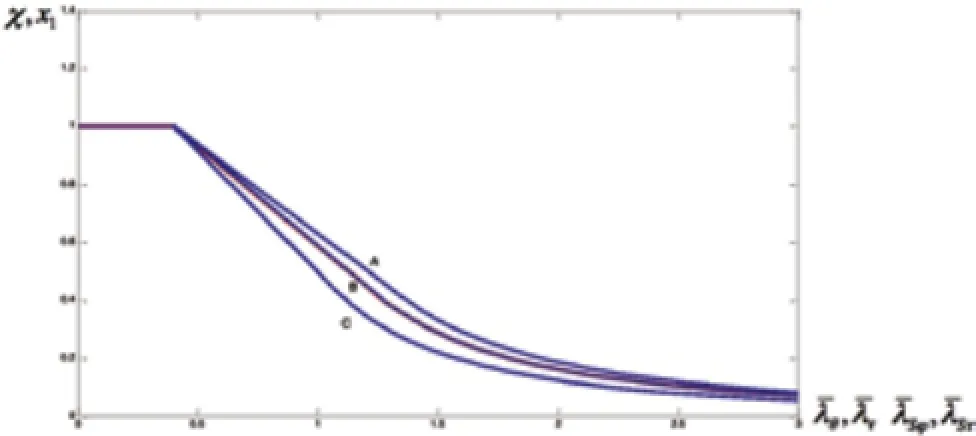
图3 环向和切向屈曲缩减系数对比图

表4 DIN18800-4和Eurocode3 1-6中屈曲缩减系数计算结果比较
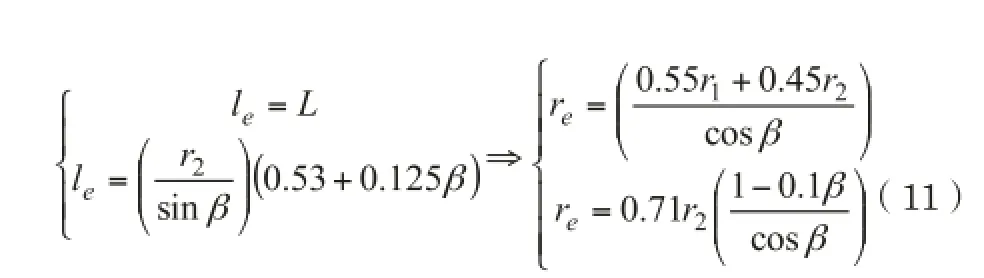
其中,L为截头圆锥的轴向长度,r1、r2是截头圆锥筒的小半径和大半径,β是半圆锥角。DIN18800-4中对于等效圆柱筒长度的要求是:

这与Eurocode3 1-6中等效半径计算公式计算结果差别很小。从屈曲相关膜应力设计值的方向来说,Eurocode3 1-6中指出,如果环向应力不是由均匀外压引起的,那么可用一个虚拟的包络应力分布σθ,Ed,env(x)来代替实际应力分布σθ,Ed(x),要求σθ,Ed,env(x)的形式符合由一个虚拟的均匀外压引起。DIN18800-4中要求计算圆锥型壳体有效膜应力时按照下式计算,这实际上是虚拟了一个均匀的环向压力所产生的膜应力,其大小包络实际压力,可见与Eurocode3 1-6中是一致的。

3 结论
本文分析了Eurocode3 1-6和DIN18800-4两部标准在风电机组塔架屈曲分析方法中各要素的区别和联系,以及计算结果的差异。总结全文,可得出以下几点结论:
(1)Eurocode3 1-6和DIN18800-4两部标准的理论基础是相同的,计算过程是十分类似的,DIN18800-4大部分过程相对来说采取了更为简化的计算方法;
(2)综合考虑各关键因素的计算方法可发现两部标准对于不同应力种类、不同壳体形式的结构,计算结果的差异存在不确定性;
(3)当塔筒制造质量等级取A级或B级并使用经济算法时,Eurocode3 1-6中的计算方法得到的三种极限屈曲应力(Eurocode3 1-6中定义为“设计屈曲应力”)很可能大于DIN18800-4的方法。
[1]马丽红,海涛,大同,东远. 兆瓦级风电机组塔筒设计分析[R].清洁高效燃煤发电技术协作网2008年会,2008.
[2]Eurocode 3 -Design of teel structures Part 1-6: Strength and Stability of Shell Structures. EN 1993-1-6:2007.
[3]DIN18800 Part 4 Structural steelwork Analysis of safety against buckling of shells.Deutsche norm.November,1990.
Contrast Research of Eurocode3 1-6 and DIN18800-4 in Wind Turbine Tower Buckling Analysis
Wang Lu
(China General Certifcation Center, Beijing 100013, China)
At present, The theoretical calculation methods are widely used for buckling analysis of wind turbine tower . The European standards Eurocode3 1-6 and the German standards DIN18800-4 are two kinds of theoretical calculation methods commonly used,both of them have great guiding signifcance on the problem of anti-buckling in design of wind turbine tower, at the same time,they are analogous in calculation concept. In this paper, the parts of these two standards with related to anti-buckling design of wind turbine tower are compared and analysised, providing a reference for related research.
tower; buckling; theoretical calculation methods; methods comparation
TM614
A
1674-9219(2013)12-0108-05
2013-10-30。
王露(1987-),女,硕士,工程师,主要从事风电机组整机认证工作。

