基于动量叶素理论改进的叶片气动特性计算方法

田德，蒋剑峰，邓英，李大宝，雷航

（新能源电力系统国家重点实验室（华北电力大学），北京 102206）

基于动量叶素理论改进的叶片气动特性计算方法

田德，蒋剑峰，邓英，李大宝，雷航

（新能源电力系统国家重点实验室（华北电力大学），北京 102206）

为实现快速计算叶片给定运行攻角所需要的桨距角，提出了一种基于动量叶素理论改进的叶片气动特性计算方法，该方法的优势为在迭代计算轴向诱导因子与切向诱导因子过程中减少了查询翼型气动特性的次数。改进的动量叶素理论计算方法比经典动量叶素理论计算方法，能够快速计算实现叶片运行攻角所需要的桨距角。利用该方法对叶片气动特性进行的计算结果与GH Bladed软件的计算结果十分接近，且提高了计算速度。

动量叶素理论；叶片气动特性；改进计算方法；提高计算速度；风电机组

0 引言

风轮是风电机组将风能转化为旋转机械能的关键部件，叶片作为风轮的主要部件，直接影响风电机组的载荷及风能吸收效率[1]。风电机组叶片气动特性的计算一直是国内外研究的热点，由此发展了一系列理论[2]。1865年Willian Rankin[3]提出了动量理论，但只考虑了轴向动量变化；1920年Albert Betz提出了Betz极限；之后发展了动量叶素理论及其修正[4-6]，涡流理论[7]等。目前可用于风电机组叶片气动特性计算的方法很多，如基于动量叶素理论的方法，基于涡流理论的方法，计算流体力学（CFD）方法等，但基于动量叶素理论的方法具有理论相对简单，计算速度快等优点，应用较广。GH Bladed软件是基于动量叶素理论开发的用于风电机组性能和载荷计算的商业软件。

经典动量叶素理论在迭代计算轴向诱导因子与切向诱导因子的过程中需要不断查询翼型的气动特性，不能够快速计算给定运行攻角所需的桨距角。因此为实现叶片运行状态控制，需要对动量叶素理论气动特性计算方法做一些改进。

1 动量叶素理论计算方法

1.1 经典动量叶素理论计算方法

利用动量叶素理论计算叶片气动特性的一般步骤：

（1）假设轴向诱导因子a和切向诱导因子b的初值，一般取a=b=0；

（2）计算半径r处叶素的入流角和攻角：

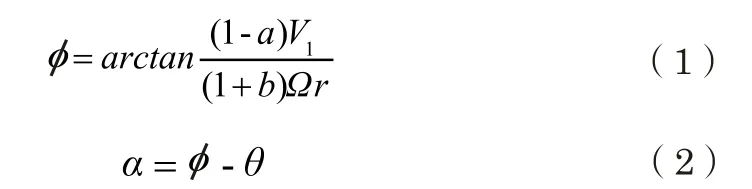
（3）根据翼型空气动力特性曲线得到叶素的升力系数Cl和阻力系数Cd；

（4）计算半径r处叶素的法向力系数Cn和切向力系数Ct：

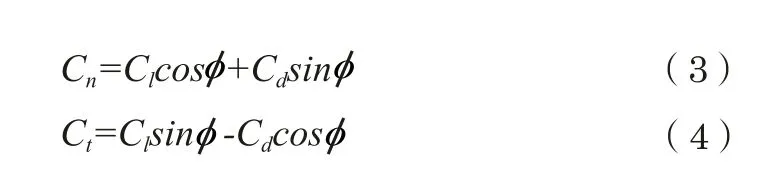
（5）计算轴向诱导因子a和切向诱导因子b的新值：

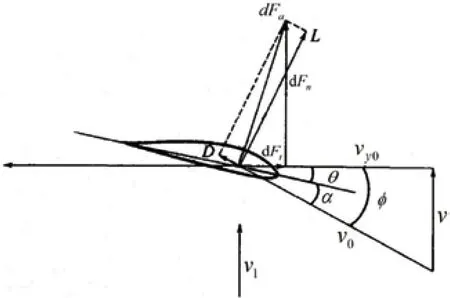
图1 动量叶素理论受力分析图

（6）将计算得到的轴向诱导因子a和切向诱导因子b的值与上一次计算的轴向诱导因子a和切向诱导因子b的值进行比较，如果误差小于设定的误差值（一般可取0.001），则迭代终止；否则，再回到步骤（2）继续迭代。

1.2 改进的动量叶素理论计算方法

改进的动量叶素理论计算方法计算叶片气动特性的一般步骤：

（1）给出叶片攻角α以及在该攻角下的升力系数Cl和阻力系数Cd；

（2）假设轴向诱导因子a和切向诱导因子b的初值，一般取a=b=0；

（3）计算半径r处叶素的入流角和桨距角：

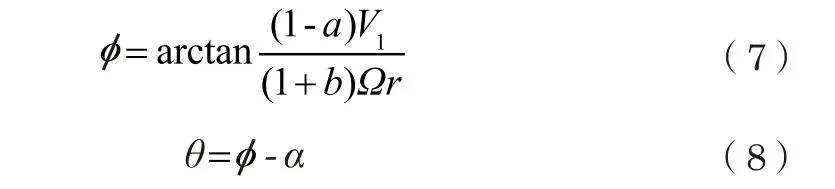
（4）计算半径r处叶素的法向力系数Cn和切向力系数Ct：

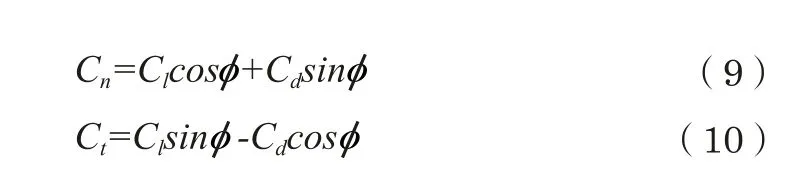
（5）计算轴向诱导因子a和切向诱导因子b的新值：

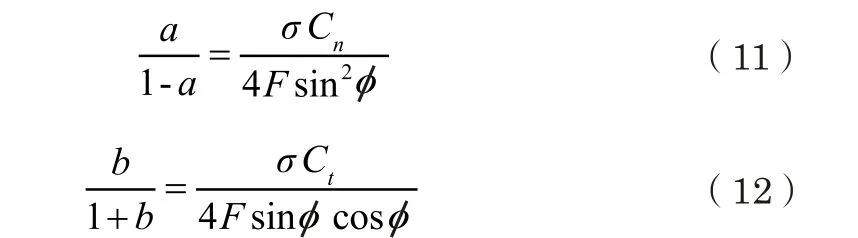
（6）将计算得到的轴向诱导因子a和切向诱导因子b的值与上一次计算的轴向诱导因子a和切向诱导因子b的值进行比较，如果误差小于设定的误差值（一般可取0.001），则迭代终止；否则，再回到步骤（2）继续迭代；

（7）将在攻角α下计算得到的桨距角θ与叶片在半径r处的桨距角进行比较，若误差小于设定的误差值（一般取决于翼型气动特性攻角的间隔），则半径r处的运行攻角就是α，否则回到步骤（1）改变攻角α的值继续进行计算。

1.3 两种计算方法对比

经典动量叶素理论计算方法是在已知叶片运行状态的情况下，即运行叶尖速比、风轮转速和叶片桨距角。假设轴向诱导因子和切向诱导因子的初值，计算入流角，再计算得到攻角，由攻角查找翼型的升力系数与阻力系数，计算得到新的轴向诱导因子和切向诱导因子，重复这个过程直到轴向诱导因子和切向诱导因子收敛为止。特点是在迭代计算轴向诱导因子和切向诱导因子的过程中需要不断查询攻角对应的升力系数与阻力系数。

改进的动量叶素理论计算方法也是在已知叶片运行状态的情况下进行计算，即运行叶尖速比、风轮转速和叶片桨距角。但需要先给出假定的叶片运行攻角，得到在此攻角下的升力系数与阻力系数，假设轴向诱导因子和切向诱导因子的初值，经过迭代计算得到轴向诱导因子和切向诱导因子以及在此攻角下所需要的桨距角，然后将计算得到的桨距角与实际桨距角进行比较，误差太大就改变攻角继续计算，误差小于设定值就得到了运行攻角、轴向诱导因子和切向诱导因子。特点为在迭代计算轴向诱导因子和切向诱导因子的过程中减少了查询攻角对应的升力系数与阻力系数的次数，由步骤（1）到（6）还能够快速计算给定运行攻角所需的桨距角。

2 计算算例

使用两种方法计算GH Bladed实例中2MW机组叶片的气动特性，叶片长度为38.75m，叶片参数如表1所示。

对功率系数Cp与转矩系数CM分别乘以修正系数0.97进行修正，对推力系数CT乘以修正系数1.015进行修正。

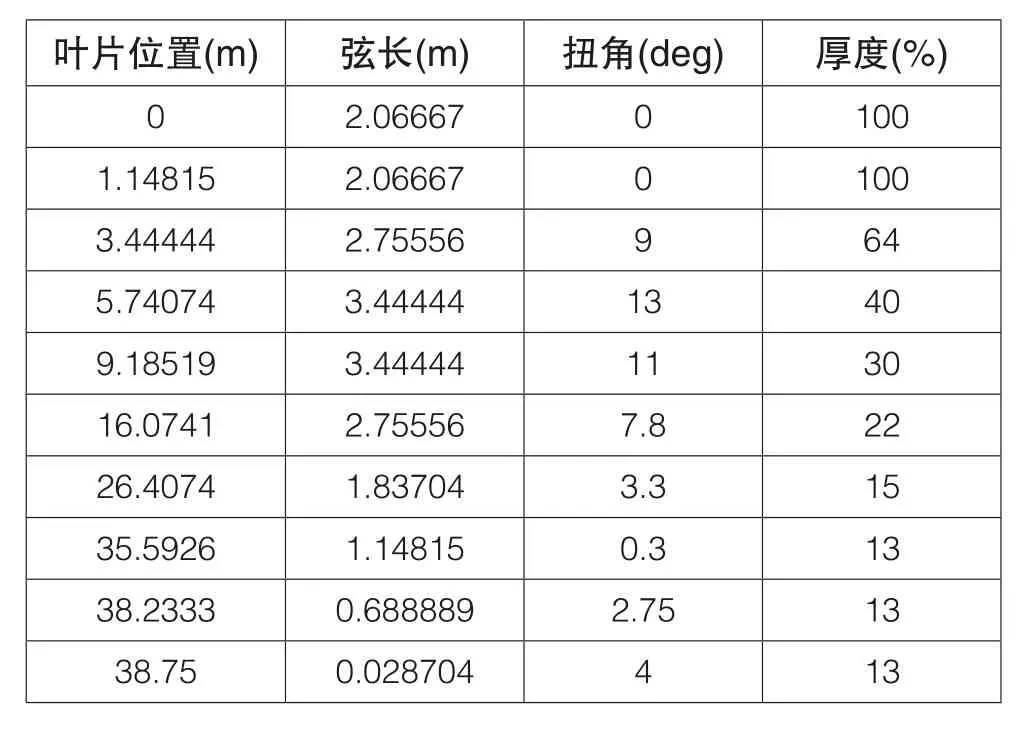
表1 计算实例叶片参数

2.1 Cp-λ曲线对比

从图2中功率系数Cp随叶尖速比的变化规律中可以看出，使用两种计算方法计算功率系数的结果在机组运行叶尖速比范围内十分接近。功率系数随着叶尖速比的增大达到一个最大值，然后功率系数随着叶尖速比的增大反而减小。

2.2 CT-λ曲线对比

从图3中推力系数CT随叶尖速比变化规律中可以看出，使用两种计算方法计算推力系数的结果十分接近。在桨距角为－2°、2°时，推力系数随着叶尖速比的增大而增大。

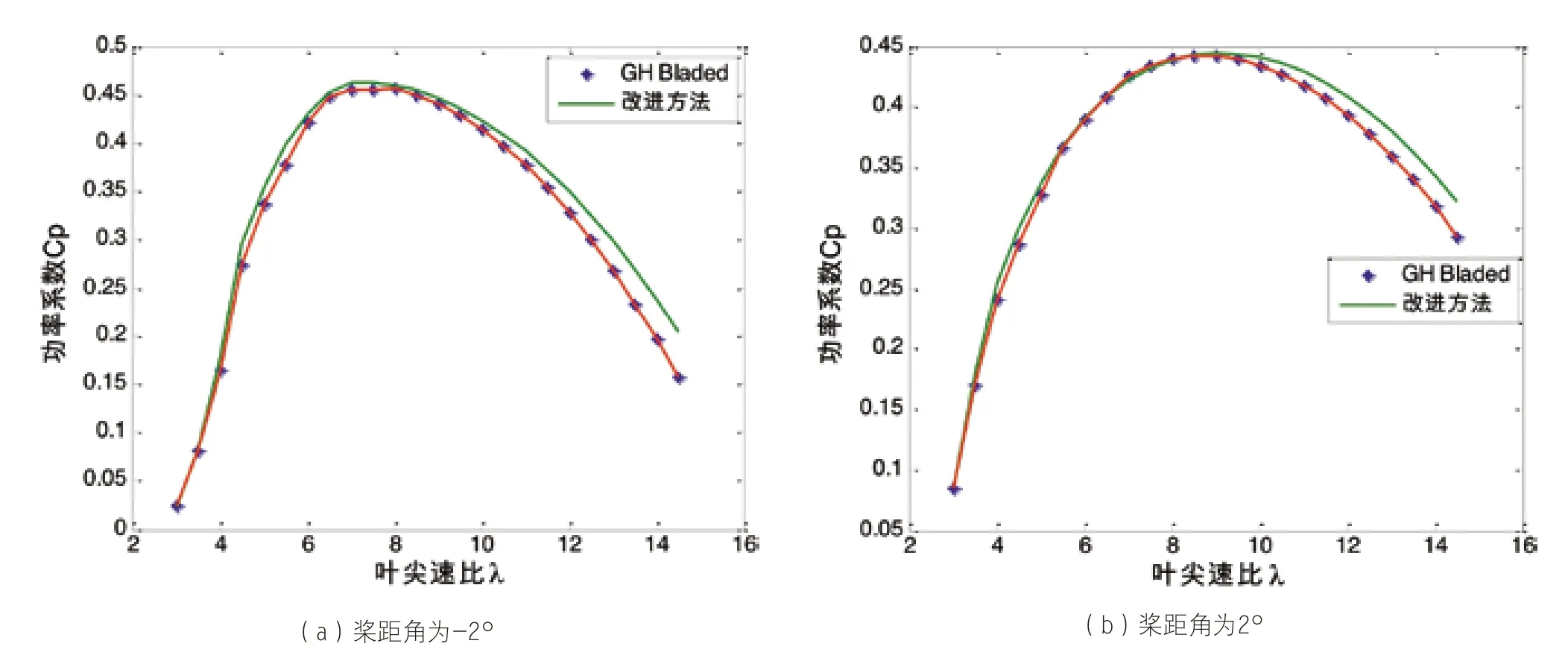
图2 桨距角为-2°、2°时，功率系数Cp随叶尖速比变化

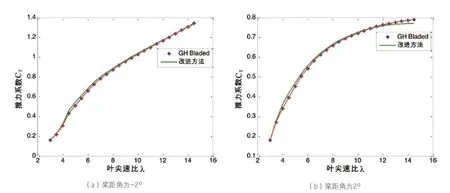
图3 桨距角为-2°、2°时推力系数CT随叶尖速比变化

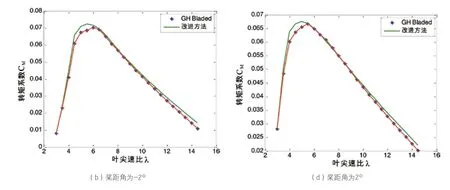
图4 桨距角为-2°、2°时转矩系数CM随叶尖速比变化

2.3 CM-λ曲线对比

从图4中转矩系数CM随叶尖速比变化规律中可以看出，使用两种计算方法计算转矩系数的结果保持着一致性且十分接近。转矩系数随着叶尖速比的增大达到一个最大值，然后转矩系数随着叶尖速比的增大反而减小。

2.4 轴向诱导因子a与切向诱导因子b分布对比

从图5可以看出，使用两种方法计算在桨距角为0°叶尖速比为6、9时的轴向诱导因子a十分接近，计算的切向诱导因子b也十分接近。

3 结论

（1）通过与GH Bladed的计算结果进行对比，说明基于动量叶素理论改进的气动计算方法是有效的。

（2）改进的动量叶素理论气动计算方法在迭代计算轴向诱导因子和切向诱导因子的过程中减少了查询攻角对应升力系数与阻力系数的次数。

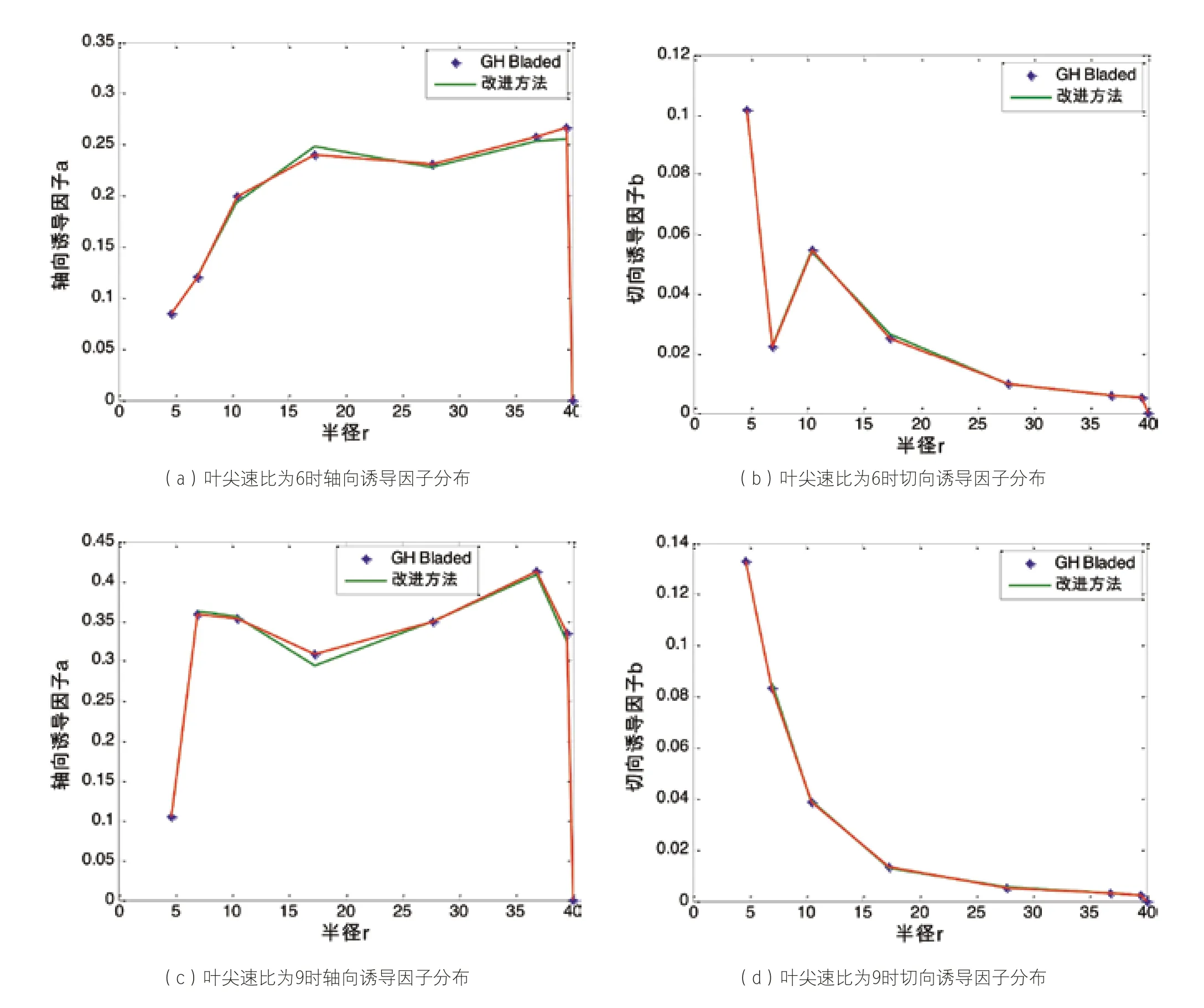
图5 桨距角为0°在叶尖速比为6、9时轴向诱导因子a与切向诱导因子b沿半径变化规律

（3）改进的动量叶素理论计算方法能够快速计算叶片给定运行攻角所需的桨距角及变桨角。

[1] 姚兴佳,田德.风力发电机组设计与制造[M].北京：机械工业出版社, 2012.

[2] De Tian, Shuo Ming Dai, Si Liu, Ning Bo Wang. Analysis of Aerodynamic Performance for Wind Turbine Based on Amended Calculation of BEM Theory[C].2nd International Conference on Energy, Environment and Sustainable Development.2012.10. pg.775-780, Jilin, China.

[3] Glauert,H.Airplane Propellers. Aerodynamic Theory[M].Berlin:Springer Verlag,1934.

[4] Tony Burton, David Sharpe, Nick Jenkins, Ervin Bossanyi. Wind Energy Handbook[M].England:John Wiley & Sons,2001.

[5] Martin O.L.Hansen. Aerodynamic of wind turbine[M].UK and USA:Earthscan,2008.

[6] P.J.Moriarty,A.C.Hansen.AeroDyn Theory Manual[M]. National Renewable Energy Laboratory,2005.

[7] Goldstein,S.On the Vortex Theory of Screw Propeller[C].Proc,Roy.Soc.1929.

Improved Calculation Method of the Blade Aerodynamic Characteristics Based on Blade Element Momentum Theory

Tian De, Jiang Jianfeng, Deng Ying, Li Dabao, Lei Hang
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources（North China Electric Power University）,Beijing 102206, China)

To achieve rapid calculation of the blade pitch angle when given the operation athack angle, an improved calculation method of blades aerodynamic characteristics based on blade element momentum theory is proposed. The advantage of this method is that it reduces the times to query the airfoil aerodynamic characteristics in the process of iterative calculation for axial induced factor and tangential induced factor. The calculation of the pitch angle of the blades when given the athack angle with the improved method is faster than that with the classical blade element momentum theory. The calculating results of the blade aerodynamic characteristics with this improved method and GH Bladed software are consistent, and the computing speed is improved with the improved method.

blade element momentum theory; blade aerodynamic characteristics；improve calculation method; improve the computing speed; wind turbine

TM614

A

1674-9219(2013)11-0088-05

2013-10-06。

田德（1958-），男，博导，教授，研究方向为风力发电系统理论与技术。蒋剑峰（1988-），男，硕士，主要从事新能源综合利用研究。

邓英（1959-），女，教授，研究方向为风力发电系统控制技术。

李大宝（1989-），男，硕士，主要从事叶片设计及风轮出力特性研究。雷航（1988-），男，硕士，主要从事风电机组载荷计算相关研究。