在尝试探索中学会推理
2012-12-29 00:00:00徐建平邵汉民
教学月刊·小学数学 2012年1期


【设计背景】
塔塔利亚是16世纪意大利著名数学家、军事科学家,编了许多数学题,这些题目都很有趣。其中一则关于猫和老鼠的题目,在解决问题的过程中,可以让我们逐步感受到尝试与推理相结合的数学探究方法的内在魅力。下面是具体的题目:
13只老鼠围成一圈,其中有一只白老鼠,一只白猫要吃掉其中的12只老鼠。
它从某只老鼠开始数数,依某个方向数到13时,就吃掉这只;剩下12只老鼠,白猫从刚吃掉的那只老鼠继续往前,从1开始数数,按照原来的方向,数到13时,就吃掉那只;然后又数数……一直进行下去,直到剩下一只老鼠为止。
试问:怎样能使白老鼠不被吃掉?
这道题目并不难,只要耐心尝试,就可以找到不被吃掉的白鼠的位置。在尝试的过程中,引导学生思考:被先后吃掉的老鼠之间有怎样的位置关系?如果改变猫吃老鼠的起点,白鼠的位置应该怎样发生变化?在数几只吃一只规律不变的情况下,增加或减少老鼠的总只数,又有什么规律?……学生通过对以上这些问题的思考,可以促进其逻辑推理能力的发展。
(本内容作为社团活动可以在五下年级进行,全班性的数学活动适合在六下年级进行。)
【教学目标】
1. 通过塔塔利亚小白鼠名题的探究,让学生初步体会运用尝试法来解决问题,并且在尝试的过程中,能自觉地发现并应用规律。
2. 经历尝试、猜测、验证等活动过程,发展学生观察、比较、推理等思维能力。
3. 在尝试探究解决问题的过程中,培养学生良好的思维品质与思维习惯。
【活动过程】
一、 激趣引题,理解题意
1. 激趣引题
教师课件出示有关猫和老鼠的图片。
师:猫和老鼠之间会发生什么故事呢?这节课我们就来研究“猫和老鼠”的数学故事。
教师课件出示题目第一部分:13只老鼠围成一圈,其中有一只小白鼠,一只白猫要吃掉其中的12只老鼠,它从某只老鼠开始数数,按某个方向数到13时,就吃掉这只。
师:同学们自己读一读,想一想是什么意思?
学生说一说,教师用手比划。
2. 理解题意
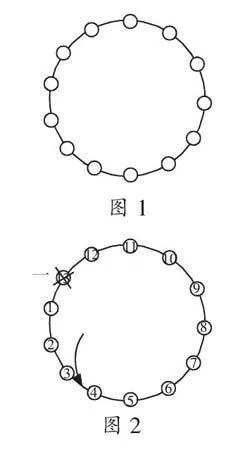
师:如果能画一张图,或许就更清楚了。老师这里就有这么一张图,你能看懂吗?(课件出示图1)
师:这些小圆圈就表示老鼠,白猫可以任选一个位置开始数数,可以按顺时针或逆时针方向数。为了便于大家交流,今天我们就让白猫乖乖地都按逆时针方向数,并按数数的方向,把所有的老鼠也都编上号。
师:现在白猫可以开始数数吃老鼠了,那白猫第一次吃掉的会是几号老鼠呢?
生:13号。
教师边指边数,进行验证。(课件逐步演示成图2)
(点评:教师用“猫和老鼠”的故事创设了有趣的情境,更容易激发学生探究的兴趣。题目内容较长,如果整体出示题目,不利于学生理解。教师将题目分段出示,并数形结合,辅以图示帮助学生更为直观地理解题意。在学生理解第一段题意后,让学生初步尝试回答白猫第一次吃掉几号老鼠,并通过边指边数进行验证,让全体学生都能掌握白猫“逢13吃一只老鼠”的规则。)
二、 尝试探究,发现规律
1. 尝试操作
(1) 尝试吃第二只老鼠
师:吃掉一只老鼠后,现在剩下几只?
生:12只。
师:白猫接下去要干什么?
教师课件出示题目第二部分:剩下12只老鼠,白猫从刚吃掉的那只老鼠继续往前,从1开始数数,按照原来的方向,数到13时,就吃掉那只。
师:这次从哪里开始数数?
生:1号。
师:你认为这次会吃掉几号老鼠?
指名学生边指边数,标出第二次被吃掉的老鼠。
(2) 尝试吃第三只老鼠
师:第二次吃掉了1号老鼠,白猫接下去又会做什么呢?
教师课件出示题目第三部分:然后又数数,如此反复,一直进行下去,直到剩下一只老鼠为止。
师:想一想是什么意思?
生:白猫继续数数,数到13时,就吃掉这只老鼠。就这样一直数下去,直到剩下一只老鼠才停止。
师:现在从哪只老鼠开始数数,吃掉的是几号老鼠?请在作业纸上标出。(3号)
学生在作业纸上边指边数,标出第三次被吃掉的老鼠。
(点评:在顺利地判断出白猫第一次吃掉的是13号老鼠后,往往会有学生误认为白猫下一次是从被吃掉的那只老鼠开始数起。于是教师并没有完全放手让学生去继续尝试。而是引领学生逐次尝试吃掉第二、三只老鼠,并请学生边指边数,在作业纸上标出被吃掉的老鼠。有了这样的尝试操作,将复杂的问题逐步分解,积累活动经验,进一步加深了学生对题意的理解。)
2. 提出问题
教师课件出示问题:怎样才能使白老鼠不被吃掉?
师:其实问题就是在问要使白老鼠不被吃掉,应该排在哪个位置。我们可以怎样来解决这个问题?
生:继续尝试,直到剩下一只老鼠为止,剩下的那只老鼠就是小白鼠。那我们就知道它最初应该排在什么位置了。
(点评:有了前面的铺垫,教师再提出最后的问题“怎样才能使白老鼠不被吃掉”,引导学生初步感悟,可以继续尝试,从最后结果中倒推出小白鼠的最初位置,培养学生的逆向思维能力。)
3. 积累经验
师:好的,那我们就继续尝试。现在还剩几只老鼠,第四次从哪里数起,你猜会吃掉哪只老鼠?请标在作业纸上。(6号)
学生自己数数验证(如图5)。
师:现在还剩几只老鼠?接下去从哪里数起,你猜第五次会吃掉哪只老鼠?(10号)
学生自己数数验证。
师:同学们真了不起,猜得这么准。莫非你们发现了什么规律?
学生观察图示,交流规律。
规律表述1:被吃掉老鼠之间间隔数每次多一个的规律。
规律表述2:数一圈多几就再数几的规律。
规律表述3:用13除以剩下老鼠只数,看余数的规律。
(点评:在学生积累了一定的操作活动经验后,教师让学生在操作前先猜一猜被吃掉的会是哪只老鼠,能调动部分学生观察比较、探求规律的积极性。在两次猜测验证后,教师的激励大大激发了学生探究规律的兴趣。对于规律的表述,则是仁者见仁、智者见智,教师允许学生根据自己的理解来表达,培养学生的个性思维。)
4. 剖析规律
师:为什么会产生这样的规律呢?
教师引导学生发现:第一次13只老鼠围成一圈时,数13个数,刚好一圈数完,不用再数了,便吃掉最后一只13号老鼠;第二次剩12只时,数13个数,数了一圈不够,还要再数一个数,便吃掉这圈中的第一只老鼠(1号);第三次剩11只时,数13个数,数了一圈不够,还要再数2个数,便吃掉这圈中的第二只老鼠(3号)……依次类推。
根据学生回答,逐次板书:13+0=13
12+1=13
11+2=13
……
师:如果发现了其中的规律,那我们接下去每吃一只老鼠,除了可以一只一只数,每数到13就吃掉一只老鼠,还可以先判断数几圈后还要再数几个,便能知道吃掉哪只老鼠了。由此看来,数数既可以一个一个地去数,也可以有规律地去数。
(点评:在教学中,教师要让学生知其然,更要知其所以然,揭示其内在本质。本教学环节中,教师就引领学生用题中绕圈数数的方法,去剖析规律的内在成因,并将直观感性的绕圈数数,抽象成简洁理性的算式,使学生感悟到余数的妙用,提升学生的思维能力。)
5. 体验规律
师:用你自己喜欢的数数方法继续尝试,看看小白鼠要不被吃掉,最初应该排在哪里?
学生继续尝试操作,解决问题。同时谈谈操作活动的经验体会。
(点评:通过规律的剖析,大部分学生已能运用规律解决问题,但教师仍提出让学生用自己喜欢的方法解决问题,较好地顾及到了班内的部分学困生。最后教师还让学生谈活动经验,促进更多学生的思维发展。)
6. 变式提升
(1) 如果白猫最初从3号位置开始数数,那小白鼠应该躲到哪个位置上?
(2) 如果白猫最初从9号位置开始数数呢?
(3) 如果小白鼠在11号位置,白猫不把它吃掉,应该从哪里开始数起?
(点评:教师设计的三个变式练习,并不是让学生去套用前面探究的规律,而是激发学生去发现白猫与小白鼠的位置关系,并根据它们的位置关系进行推算,培养学生的推理能力。前两题,要学生推算出小白鼠随着白猫位置变换而变化的安全位置。最后一题则是从小白鼠的位置去倒推白猫的位置,培养学生的逆向思维能力。)
7. 小结提炼
师:通过这个复杂问题的解决,你有什么经验要与同学分享?(学生自由说)
小结:正如同学们所说的,在遇到复杂问题时,很多时候需要勇于思考,敢于尝试,善于发现和运用规律,化繁为简,从而解决问题。
三、 应用深化,拓展延伸
1. 应用深化
师:老师也改编了几道猫吃鼠的问题。
(1) 出示题组
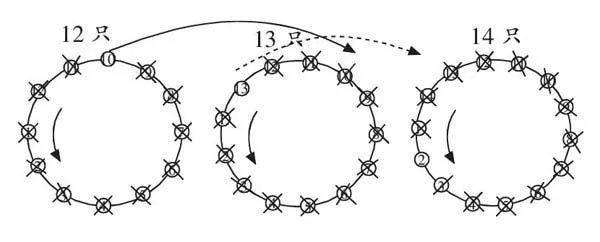
①12只老鼠围成一圈,按逆时针方向数到3时,就吃掉一只老鼠,如此反复,最后剩下的那只老鼠最初应该排在( )号位置。
②13只老鼠围成一圈,按逆时针方向数到3时,就吃掉一只老鼠,如此反复,最后剩下的那只老鼠最初应该排在( )号位置。
③14只老鼠围成一圈,按逆时针方向数到3时,就吃掉一只老鼠,如此反复,最后剩下的那只老鼠最初应该排在( )号位置。
(2) 读一读,比一比:这三题有哪些异同点?
(3) 引发思考:这三题中都是每数到3就吃掉一只老鼠,不同的是老鼠总数每次增加了一只,似乎很有规律,那最后幸存者的位置会不会也有某种规律呢?
(4) 小组合作完成(组内每人做一题)。
(5) 反馈交流,探究规律。
出示答案,引导学生观察图示,探究规律:每增加一只老鼠,幸存者的位置就向前移动3个。
2. 应用规律
(1) 15只老鼠围成一圈,按某个方向数到3时,就吃掉一只老鼠,如此反复,最后剩下的那只老鼠最初应该排在( )号位置。
(2) 11只呢?
师:最后幸存者的位置每次移动3个,而不是4个、5个,这可能跟什么有关?为什么会有这样的规律呢?感兴趣的同学,课后可以与老师一起再探讨。
(3) 把“塔塔利亚的小白鼠”问题中的“13只老鼠围成一圈”,改成“14只老鼠围成一圈”,那小白鼠要想不被吃掉,应该排在哪里?
(点评:这一环节的设计,不仅仅是单纯的应用练习,更重要的意图是延续的思维,深化猫吃鼠问题的规律。让学生在观察比较、沟通联系中,去发现此类问题更多的内在关联,发散学生思维。)
3. 拓展延伸
师:诸如此类猫吃鼠的问题,在西方也叫做“约瑟夫斯问题”,在中国称作“八仙落座问题”。
我国古代数学专著中有这么一题:环二十子,内有二黑子相连。以九数之,止处即除一子。除毕,二黑不动。宜从何处起?
(1) 读一读,比一比:这题与前面的问题最大的不同之处是什么?
(2) 学生尝试解决。
(3) 反馈交流。
(点评:链接相关史料,赋予数学问题浓浓的文化气息,让学生了解到塔塔利亚的小白鼠问题的历史渊源。学生在相关史料的学习中,进一步知道了其变式与拓展演变,拓宽了视野,厚实了数学社团活动的文化底蕴。)
四、 回顾总结,拓展思维
师:这节课我们研究了什么问题?你有什么收获?
教师总结:像塔塔利亚的小白鼠这类问题,其中的规律奥秘远不只我们这节课所探讨的,已有许许多多的人对此深入研究过,还根据其内在规律,编制出了电脑计算程序,可以用于解决数据更大的此类问题。
(浙江省杭州市萧山区长沙小学 311200
浙江省杭州市萧山区教研室 311200)

