论布鲁尔SMK思想及其对当代数学教育的意义

　　布鲁尔的SMK（sociology of Mathematic Knowledge）思想是其SSK（sociology of scientific knowledge）思想的重要组成部分，其内涵在于指出并不存在独立于环境的所谓理性范式，即便数学知识具有很强的理论性和逻辑自恰性，也应该对它进行社会学分析；社会力量对于最深奥、最抽象的数学领域也能够施加有力的影响，数学的威力就在于其中不可剔除的社会性成分。他以2+2=4为例，对其进行了具体的社会学分析；在这之前，他首先予以明确。
　　一、对2＋2＝4进行社会学分析具有可能性
　　“2+2=4这些术语的意义清澈如晶体，毫无弹性，以致命题只有单一的解释，其真实性丝毫不容反驳，千秋万世，显示着理性所固有的洞烛真伪的能力”[1]，事实果然如此？
　　对此，知识社会学创始人卡尔·曼海姆（Karl Mannheim）明确指出，自然科学中质的方面所包含的因素或多或少与认知主体的世界观交织在一起，但是“它的可定量领域，在很大程度上可以超脱于研究者的历史——社会视角。”比如数学的历史发展“在很大程度上决定于内在的因素。”因为数学知识有特殊的认识论地位，它与研究者的历史社会观在很大程度上是脱离的，对它的研究不受研究者观念形态的影响，它是可以逃避思想批判的知识形式，无法对其进行社会学的分析，因而需要从知识社会学的研究视野中将其剔除。
　　布鲁尔否定曼海姆的这种观点，他认为数学知识并不具备社会学分析的豁免权，因为我们无法在物理、化学等经验性知识和通常认为的包括数学、逻辑学在内的非经验性知识之间做出区分，更不能将不同的心智器官视为不同知识的产生源泉，比如说感觉经验器官产生关于经验事实的有条件的知识，而理性的器官则产生关于逻辑和数学必然性的真理。
　　布鲁尔以因果性、公平性、对称性等原则构成的纲领为理论平台，指出并不存在超文化的所谓的理性范式，对于数学知识也应该进行社会学分析，从而将因果性指导原则推及到了传统上认为是自然科学知识中的硬核部分——数学领域，“我们至今所讨论的问题以及问题讨论的结论将从经验知识领域和有条件的知识领域，扩展到‘必然性’真理的王国”。所以对包括2+2=4这样的数学知识也是可以进行社会学的分析的。
　　另外，为了批判2+2=4具有意义确定性的观点，布鲁尔还理性地构建了语境。他认为2+2=4这个式子的含义并非如理性主义者所想的那样确切，它依赖于具体的语境，比如在他所构造的仅有0、1、2、3、4这样5个数字的有限算数（finite arithmetic）的环境中，当人们回答3+3=1，3+4=2，2*2=4，3*3=4的时候，2+2=4的意义就异于它在十进制中的意义。也即单单拿出一个孤立的式子2+2=4，实际上我们无法理解其确切、具体的含义，我们无法判断它究竟是应用于十进制还是五进制的语境中。我们不能因为五进制的应用范围小于十进制的，就认为五进制的应用不合理、没有意义。这也是布鲁尔强纲领中公正性原则的贯彻，即“它应当对真理和谬误、合理性或者不合理性、成功或者失败，保持客观公正的态度。这些二分状态的两个方面都要加以说明。”
　　二、对2＋2＝4“非社会学分析”观点的批判
　　布鲁尔采用他一贯主张的自然主义、经验主义的原则，对2+2=4的产生和建立进行了分析。他通过对2+2=4低阶（low-status）、中阶（middle-status）和高阶（high-status）三阶证明的批判，得出“2+2=4的可信性并不是建立在证明的基础之上，具有充分必要条件的证明并不存在”的结论，针锋相对地反驳了劳丹的观点——由证明产生的理性的信念是2＋2=4的可信性的根源。
　　首先，布鲁尔对2+2=4的低阶证明进行了批判。低阶证明是普通人对这个公式的认识过程。这时人们往往借助实物进行证明，从一堆苹果中选取一对儿，数数：一、二。从这堆苹果中另取一对儿，数数：一、二。然后将两对并行放置，数数：一、二、三、四。这就是2＋2=4的原因。最后的结论可能是：所有与之相似的群体都会产生与之同样的结果。于是：2+2=4。但布鲁尔认为，仅仅因为这些苹果现在以这种方式作为，并不能说明它们将会总是以同样的方式作为。如此方式建立的一个归纳和经验的真理，显然无法推延到建立2+2总是并且必须等于4这样一个永恒真理。所以，以这种方式对2+2=4进行的低阶证明，是不能成立的。
　　其次，布鲁尔对2+2=4的中阶证明进行了批判。弗雷格（Frege）和皮诺（Peano）所使用的证明用相继关系定义自然数，1是0的后继者，2是1的后继者，2也是0的后继者的后继者，等等。符号表示为：1=S（0），2=S（1），或者2=S（S（0））。这样，2+2=S（S（0））+S（S（0）），4=S（S（S（S（0））））。显然，要使用这种方法证明2+2=4，我们就要追寻S的使用次数。事实上也就是在数数，这样，在证明之初就已经预设了要证明的结果。
　　再次，布鲁尔对2+2=4的高阶证明进行了批判。职业逻辑学家麦克尔（J.L.Mackie）在1966年对于2+2=4做了一个12步的高阶证明，第1步是他用符号化的语言表达了进行低阶证明的记数者（quantifiers）的行为。后2步是对第1步信息的重复，但消解掉了记数者存在的信息。以后的几步都是对前面步骤的归约，到了第11步，他把一开始消解掉的记数者又拾了回来。第12步则表达了这样的信息，即对于K、L和M集合，如果K只有2个元素，L也只有2个元素，那么当M把两个集合合并，M就是一个四元素的集合。麦克尔的结论是，基于符号逻辑的12个步骤进行演算的这个高阶证明，与我们进行低阶证明时所依赖的完全是一样的思维过程，即我们依赖于2+2=4这个例证。
　　在布鲁尔看来，这个所谓的高阶证明不外乎是引进了a、b、c、d四个符号，a和b形成一个2元素的集合K，c和d形成一个2元素集合L，a、b、c、d则形成了一个4元素的集合M，其实，它们与低阶证明并无二致，至多前者是一个身体性的收集活动，后者是一个符号性的操作活动。显然麦克尔的证明恰恰说明2+2=4奠基于原始的社会性活动中。布鲁尔对此深刻地指出，如果说我们从建构中得到了什么，原因还是在于我们作为孩童时刻接受的训练。对于2+2=4来说，我们接受它，是因为它来自传统，来自社会性活动，而不是所谓的证明或自明。
　　这样，对于2+2=4来说，无论是低阶证明、中阶证明还是高阶证明，都是建立在社会性活动的基础上的，都可以在其中发现社会因素的存在。
　　三、布鲁尔对2＋2＝4的社会学分析及其对当代数学教育的意义
　　布鲁尔认为，2+2=4之所以具有可信性，不在于它得到了证明，而在于它是一种约定，并对这种约定的社会本性进行了如下分析：
　　布鲁尔首先将数学与语言、学习数数与学习拼写进行了类比，“我们在数数中受训，正如我们在字母中受训一样，我们学习加法就像我们学习拼写一样”，继而指出无论是学习数学还是学习语言，它们都涉及规则的遵守，“但是没有人不把字母或拼写规则视作社会约定”，“当孩子们在学习算术时，孩子们所受的训练受制于他们的老师，还有什么比在学习数数过程中坚决要求孩子必须说4之后是5，3之后是4更强烈的权威诉求吗”？而整个“传授过程必须被看作是社会性决定的和有社会性条件的”。“数学的必然性不过是通常附着于某种更重要的社会约定的道德必然性的一个种类，数学的严格性不过是一种社会需要的严格性，即这种社会需要我们使用这种技艺而不是那种技艺”。
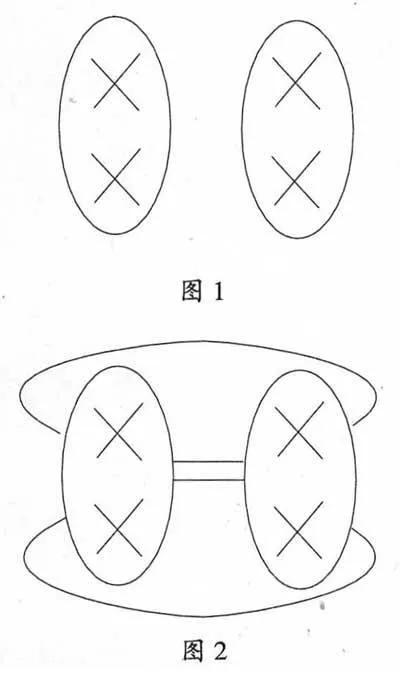
　　对于2＋2＝4的使用，已经日常化到了我们的实践当中。而对于2＋2＝4的这种约定，不外乎说明了一种我们集体所认可的方式，这从维特根斯坦的著作中可以清晰发现，“要明白2＋2＝4，你只需看一下图1”
　　这样的分类模式一定是已经训练好了的，否则为什么不是图2所示？
　　不同的分类模式正是有限论（一个词语的现今用法无法决定其将来的用法）得以建立的基础，因为人们的社会约定不同，导致分类模式相异，进而也将直接导致体现在数学认知上的差异：2+2=4？2+2=5？布鲁尔认为，事实上2+2=5一点都不离经叛道，它也不是我们大脑正常工作的剧烈破坏或者是彻底的洗脑，因为如果更换一个情境，比如拉卡托斯在《证明和反驳》一书中所设置的虚拟情景——设想一下我们要邮递两个各自重量为2磅的物品，它们被装在一个重量为1磅的盒子里递，那么在这个包裹中两个2磅就是5磅！我们朴素地认为2+2=4，是因为有着这样一个辅助的约定，即包装材料的重量为零。
　　2+2=4而不是2+2=5，这并不说明前者对应着某种神秘的数学现实，人们之所以偏爱拉卡托斯的“无重量”加法，是因为“对加法建立一个约定意味着解决一个协调问题，就是说要使每一个人适应于同一个程序”，完全是出于实用的理由。2+2=4这个经由诸多证明得出的稳定结论的意义，就在于它“具有的制度性的特征”。
　　拉卡托斯就曾经指出，说数学的某些方面、论证的某些风格呈现出永恒真理的外观，那是因为此时的数学处于常规发展时期，它的范式没有受到批判。布鲁尔也认为数学中不存在任何终极性的逻辑本质，数学与物理学、化学等其他科学一样，都可以利用猜想、反驳的方法加以研究。说数学是一目了然的，那是因为它处于一个没有受到批判的研究范式下，而来源于库恩的范式，当然为社会性因素的进入提供了方便之门！
　　可以说，教育、科技一直以来尤其现在更是我国的大事，教育观必须以科技观为先导，更具体地讲，数学教育观要以数学观为先导。而数学观作为一种理论概括，它应该与数学史的发展保持一致，逻辑的总要与历史相统一。而当前在我国数学教育中，理性推导与公式记忆的教学法一直占据主流，数学史的教学非常薄弱，而数学史以及其中形成的数学观对于数学教育的重要意义已经显而易见：改变数学枯燥、抽象的形象；加大数学文化功能的研究；提升学生人文素质的重要途径；让学生不仅知道数学之然而且知其所以然，从而为进一步创新打下坚实基础。
　　参考文献
　　[1] [英]伊姆雷·拉卡托斯.证明与反驳.上海：上海译文出版社，1987.
　　[2] [德]卡尔·曼海姆.意识形态与乌托邦.北京：商务印书馆，2002.
　　[3] [美]拉里·劳丹.进步及其问题.北京：华夏出版社，1990.
　　[4] [英]巴里·巴恩斯等.科学知识——一种社会学的分析. 邢冬梅等译.南京：南京大学出版社，2004.
　　[5] [英]大卫·布鲁尔.知识和社会意象. 艾彦译.北京：东方出版社，2002.
　　[6] 涂纪亮主编.维特根斯坦全集（7）. 徐友渔，涂纪亮译.石家庄：河北教育出版社，2003.
　　[7] 杨渭清.HPM视野下的数学教育.西安文理学院学报：自然科学版，2010（7）.
　　（责任编辑 刘永