基于有效介质理论碳纤维的介电常数计算
秦思良,王庆国,曲兆明,雷忆三
(1.军械工程学院静电与电磁防护研究所,河北石家庄 050003;2.中国电子科技集团第33研究所,山西太原 030006)
基于有效介质理论碳纤维的介电常数计算
秦思良1,王庆国1,曲兆明1,雷忆三2
(1.军械工程学院静电与电磁防护研究所,河北石家庄 050003;2.中国电子科技集团第33研究所,山西太原 030006)
采用M-G方程、Bruggeman方程和广义M-G方程计算了复合材料内碳纤维的介电常数。结果表明:当纤维长径比较大时,3个方程均可以计算出碳纤维的介电常数,并且数量级和趋势保持一致;广义M-G和M-G方程的计算结果较为一致,而Bruggeman方程则小于其余两者的计算结果;当碳纤维浓度上升至渗流浓度附近时,3个方程计算结果均出现一定程度的偏离,表明3个方程均适用于低浓度情况。
M-G方程;Bruggeman方程;广义M-G方程;介电常数;碳纤维
近年来随着电子器件的广泛应用,空间电磁环境变得日益复杂,人们对于高效电磁防护材料的需求日益迫切[1-3]。然而,在材料应用过程中,单一的电磁屏蔽材料难以同时满足低、中、高频率范围内电磁屏蔽的要求,研究发现可采用电磁材料核壳复合、多元成分屏蔽剂共混、多层涂层复合的技术获得性能更优异的新型屏蔽复合材料[4-6]。电磁屏蔽复合材料的屏蔽性能取决于其内部的填充颗粒,特别是具有各向异性的填充粒子对复合材料的有效性能影响十分显著。应用复合材料宏观有效性能的预测理论往往要求填料的本征参数为已知,因此准确测得填料本身的电磁参数对于电磁防护材料的设计具有重要意义[7-8]。许多粉体填料(如短碳纤维、球形玻璃微珠等)的电磁参数无法直接测得,往往需要添加到另一种基质中进行测试,然后通过相应公式计算反推得到填料本身的电磁参数[9]。因此,选择合适的公式模型对于准确预测填料本身电磁参数的准确性具有重要意义。
笔者基于经典的有效介质理论,应用M-G方程、Bruggeman方程 以及基于变分法得到的广义M-G方程[11-12],由不同浓度复合材料介电常数的测试值反推碳纤维本身的介电常数。通过比较不同浓度下的3个方程计算得到碳纤维本身的介电常数,确定了不同公式的适用条件,对于准确预测碳纤维的介电常数具有一定的理论价值和参考意义。
1 理论分析
M-G方程、Bruggeman方程和广义M-G方程的提出分别有各自不同的理论依据和相应假设。M-G方程假设颗粒分布为弥散微结构,即填料颗粒嵌入到基质颗粒中,不考虑颗粒之间相互作用,有效介电常数满足式(1)要求:

2 算例验证
为了比较3种不同方法对于碳纤维介电常数的预测情况,笔者针对复合材料中短碳纤维的介电常数进行了预测。通过实验测得质量分数分别为0.1,0.2,0.3时复合材料的介电常数,测试带宽均为30 MHz~6 GHz。基质材料为石蜡,介电常数ε1=2.2,短碳纤维直径为9μm,长4 mm。采用3种公式计算碳纤维的介电常数,如图1—图5所示,其中图1—图4中lgε表示介电常数实部的对数值,图5中lgε′表示介电常数虚部的对数值。
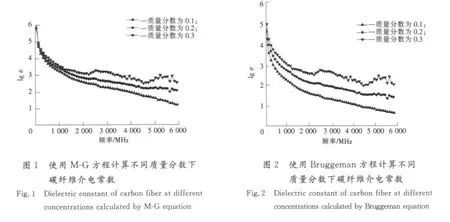
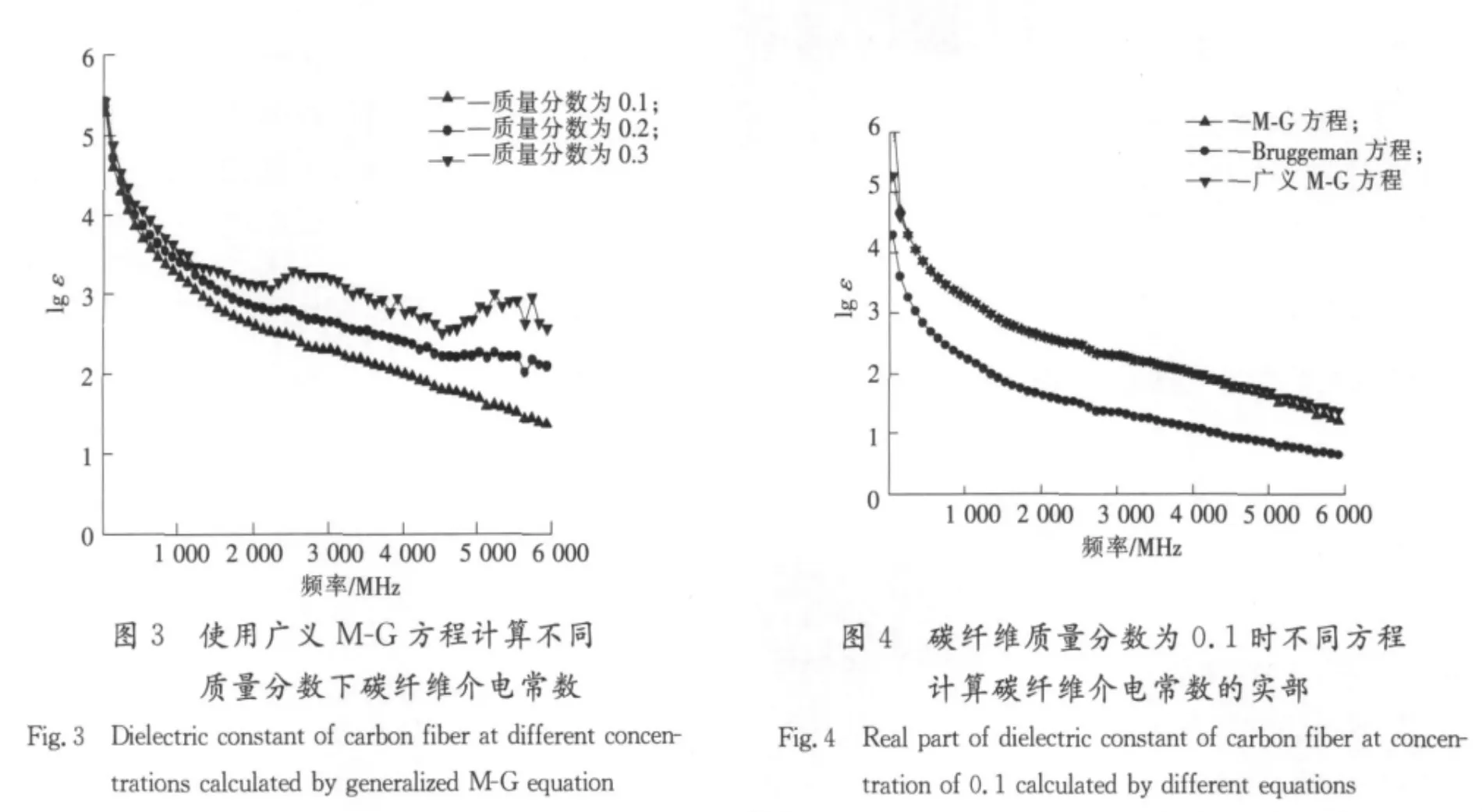
3 结果分析
由图1-图3可以看出,碳纤维质量分数为0.1和0.2时,M-G 方程、Bruggeman方程和广义M-G方程由不同浓度复合材料计算碳纤维介电常数的结果趋势一致,但是 M-G方程和广义M-G方程的计算值差异要小于Bruggeman方程的计算值差异。碳纤维质量分数为0.3时,3个方程反推碳纤维的介电常数趋势发生明显变化,在局部频段出现数值上升。这是因为当碳纤维质量分数为0.3时碳纤维之间出现了搭接和聚集,复合材料电磁性能发生渗流突变,3个方程在渗流区域均出现不同程度的失效[13-14]。
由图4、图5可以发现,M-G方程和广义M-G方程计算的碳纤维介电常数实部非常接近,而虚部在高频段出现一定分离,而Bruggeman方程的计算值要低于M-G方程和广义M-G方程。上述情况可以进行理论上的解释。对于算例中的纤维,L z=1.850 2×10-5≈0,假设碳纤维均匀分布,L v≈0,则广义 M-G方程变为

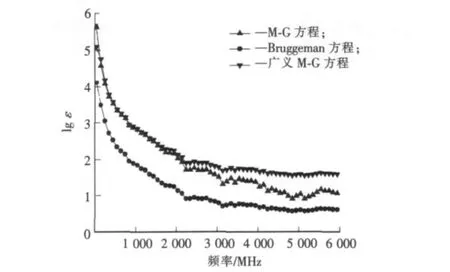
图5 碳纤维质量分数为0.1时不同方程计算碳纤维介电常数的虚部Fig.5 Imaginary part of dielectric constant at concentration of 0.1 calculated by different equations

4 结 论
1)碳纤维浓度较低时,M-G方程、Bruggeman方程和广义M-G方程均可以由复合材料介电常数计算出纤维介电常数,计算结果有一定差别,但是趋势保持一致。
2)M-G方程和广义M-G方程由不同浓度复合材料计算纤维介电常数时,不同浓度计算结果差异性要小于由Bruggeman方程计算得到的结果。
3)对于碳纤维长径比远大于1并且均匀分布的复合材料,广义M-G方程和M-G方程碳纤维介电常数计算结果较为一致,而Bruggeman方程的碳纤维介电常数计算结果要小于广义M-G方程和M-G方程。
4)当碳纤维浓度达到渗流浓度以后,3种方程均出现不同程度的失效。
[1]王祖鹏,于名讯,潘士兵.复合材料电磁参数计算的理论研究进展[J].材料导报(Materials Review),2009,23(11):246-249.
[2]陈小林,成永红,吴 锴,等.两相复合材料等效复介电常数的计算[J].自然科学进展(Progress in Natural Science),2009,19(5):532-536.
[3]马 静,陈维视,李 军.碳纳米管的结构及应用前景[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2004,25(3):30-33.
[4]邵寒梅,官建国,王一龙,等.电磁波屏蔽复合材料的研究进展[J].安全与电磁兼容(Safety &EMC),2008(1):65-69.
[5]夏艳平,陶 宇,张国庆,等.填料形貌对导热胶渗流阈值的影响研究[J].功能材料(Journal of Functional Materials),2010,41(增):357-364.
[6]孙世清,毛 磊,刘宗茂,等.Al2O3-Cu和C-Cu复合材料研究进展[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2011,22(1):177-182.
[7]魏书华,王晓军,陈雪英.混凝土受弯构件加固中碳纤维的设计和应用[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2011,32(2):177-182.
[8]陶 宇,夏艳平,张国庆,等.填料长径比对导电胶渗流阈值的影响[J].复合材料学报(Acta Materiae Compositae Sinica),2010,27(6):213-217.
[9]王秀翠,沈连婠,孙 袁,等.直线加速器同轴负载材料FeSiAl的电磁参数测试及仿真[J].强激光与粒子束(High Power Laser and Particle Beams),2011,23(1):170-174.
[10]南策文.非均质材料物理-显微结构-性能关联[M].北京:科学出版社,2005.
[11]DUAN H L,KARIHALOO B K,WANG J,et al.Effective conductivities of heterogeneous media containing multiple inclusions with various spatial distributions[J].Physical Review B,2006,73:174-203.
[12]高原文,雷芳明.吸收剂颗粒界面效应对电磁波吸收性能影响的理论研究[J].功能材料(Journal of Functional Materials),2009,40(3):372-375.
[13]KHAMFOROUSH M,SHAMS K.Percolation thresholds of a group of anisotropic three-dimensional fracture networks[J].Physica A,2007,385(2):407-420.
[14]FLORENT D,DENDIEVEL R,CHAZEAU L,et al.Carbon nanotube-filled polymer composites:Numerical simulation of electrical conductivity in three-dimensional entangled fibrous networks[J].Acta Materialia,2006,54(11):2 923-2 931.
Calculation on permittivity of carbon fiber based on effective medium theory
QIN Si-liang1,WANG Qing-guo1,QU Zhao-ming1,LEI Yi-san2
(1.Institute of Electrostatic and Electromagnetic Protection,Ordnance Engineering College,Shijiazhuang Hebei 050003,China;2.The 33rd Institute,China Electronics Technology Group Corporation,Taiyuan Shanxi 030006,China)
The permittivity of carbon fibers in different composites is calculated and discussed by using M-G equations,Bruggeman equations and generalized M-G equation.Results show that for high draw ratio fibers,all the three equations can calculate out the permittivity with the same numerical level and variation trend.Generalized M-G equation and M-G equation have a similar result but Bruggeman's result is smaller.All three equations become invalidation when fibers'concentration reaches its percolation threshold,which means that all three equations are useful at low concentration.
M-G equation;Bruggeman equation;generalized M-G equation;permittivity;carbon fiber
TM153+.5
A
1008-1542(2012)04-0309-04
2012-03-19;
2012-05-01;责任编辑:张士莹
装备预研基金资助项目(9140A31030110JB3403)
秦思良(1987-),男,河南焦作人,硕士研究生,主要从事电磁防护理论与技术方面的研究。

