具有p-Laplacian算子的分数阶微分方程边值问题
张 宁, 史小艺, 张 娣
(1.中国矿业大学 理学院,江苏 徐州 221116;2.中国矿业大学 管理学院,江苏 徐州 221116)
具有p-Laplacian算子的分数阶微分方程边值问题
张 宁1, 史小艺1, 张 娣2
(1.中国矿业大学 理学院,江苏 徐州 221116;2.中国矿业大学 管理学院,江苏 徐州 221116)
在一定条件下,利用Banach压缩映射原理讨论了具有p-Laplacian算子的分数阶微分方程边值问题解的存在性和唯一性,得到了解存在和唯一的充分条件,并举例说明了结论的适用性。
分数阶微分方程;p-Laplacian算子;Banach压缩映射原理
0 引言
近年来,分数阶微分方程在科学、工程和数学等领域得到了广泛应用,其边值问题的理论研究,获得了不少成果[1-9],值得注意的是,具有p-Laplacian算子的分数阶微分方程边值问题作为分数阶边值问题的一种情况,得到了研究者的重视,相关的研究文献很多[4-9],如文献[5]利用Banach压缩映射原理研究了具有p-Laplacian算子的分数阶微分方程边值问题
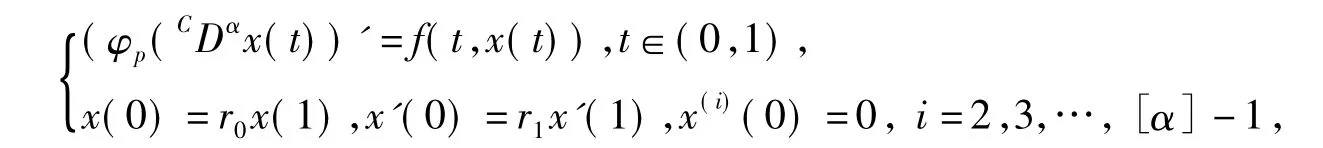
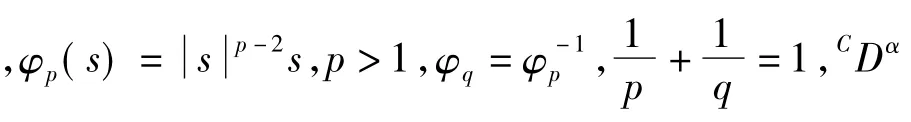
受上述文献启发,文中研究具有p-Laplacian算子的分数阶微分方程边值问题

1 预备知识
先回顾一些基本定义。
定义1[6]函数u:(0,+∞)→ 的α阶Riemann-Liouville分数阶积分为

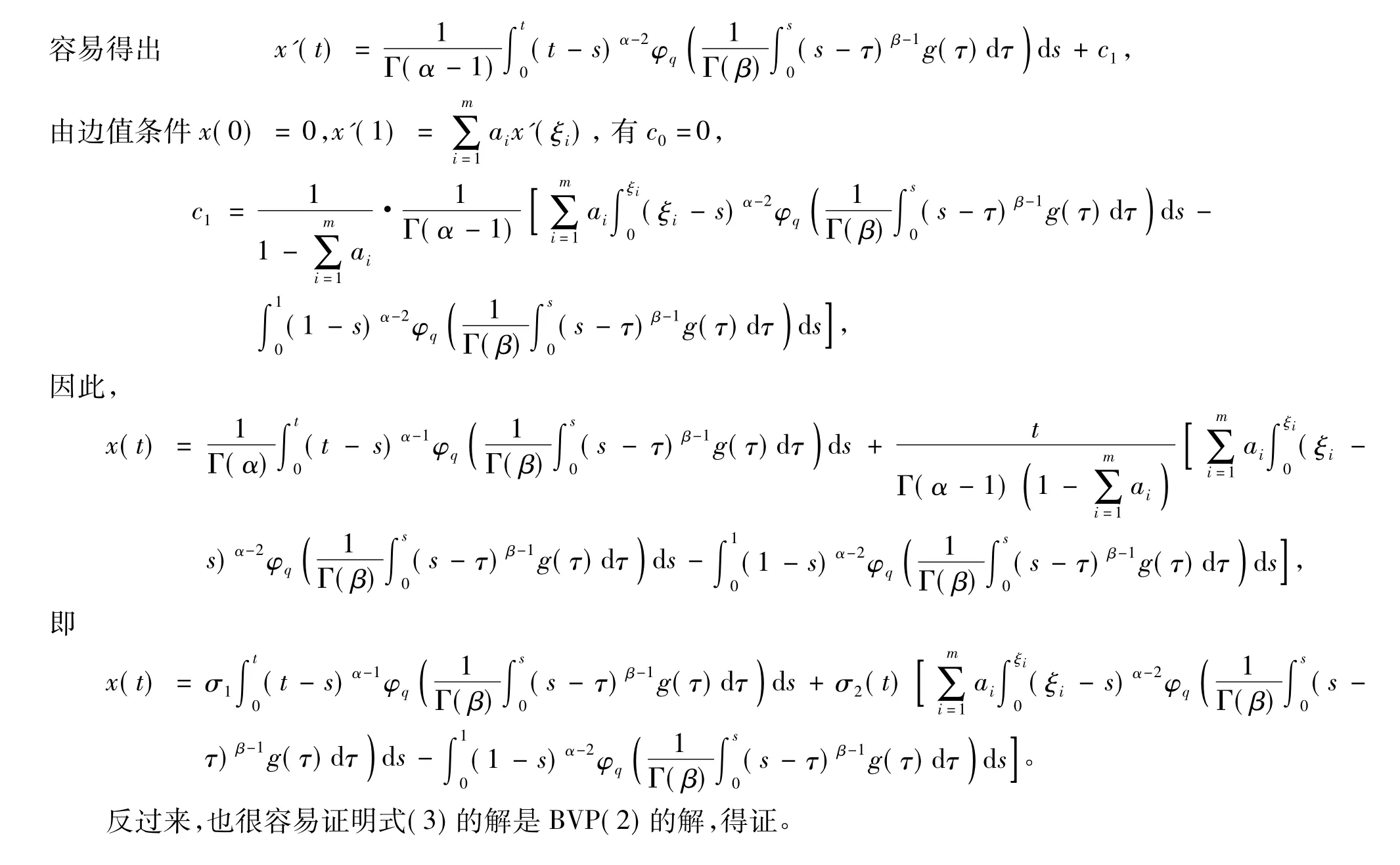
2 主要结果




3 算例


[1]AHMAD B,NIETO J J.Anti-periodic fractional boundary value problems[J].Computers & Mathematics with Applications,2011,62(3):1150-1156.
[2]BAI ZHANBING,LU HAISHEN.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].Journal of Mathematical Analysis and Applications,2005,311(2):495 -505.
[3]WANG GANG,LIU WENBIN,ZHU SINIAN,et al.Existence results for a coupled system of nonlinear fractional 2m-point boundary value problems at resonance[J].Advances in Difference Equations,2011(1):44.
[4]CHEN TAIYONG,LIU WENBIN,HU ZHIGANG.A boundary value problem for fractional differential equation with p-Laplacian operator at resonance[J].Nonlinear Analysis:Theory,Methods & Applications,2012,75(2):3210 -3217.
[5]LIU XIPING,JIA MEI,XIANG XIUFEN.On the solvability of a fractional differential equation model involving the p-Laplacian operator[J/OL].Computers & Mathematics with Applications,2012,62[2012 -03 -29].http://dx.doi.org/10.1016/j.camwa.2012.03.001.
[6]CHEN TAIYONG,LIU WENBIN.An anti-periodic boundary value problem for the fractional differential equation with p-Laplacian operator[J].Applied Mathematics Letters,2012[2012 -03 -29].http://dx.doi.org/10.1016/j.aml.2012.03.035.
[7]DU Z J,LIN X,TISDELL C C.A multiplicity result for p-Laplacian boundary value problems via critical points theorem[J].Applied Mathematics Computation,2008,205(1):231-237.
[8]HE ZHIMIN,LI LIAN.Multiple positive solutions for the one-dimensional p-Laplacian dynamic equations on time scales[J].Mathematical and Computer Modelling,2007,45(1/2):68-79.
[9]SUN BO,GE WEIGAO.Existence and iteration of positive solutions for some p-Laplacian boundary value problem[J].Nonlinear Analysis:Theory,Methods& Applications,2007,67(6):1820-1830.
Boundary value problems for fractional differential equation with p-Laplacian operator
ZHANG Ning1, SHI Xiaoyi1, ZHANG Di2
(1.College of Sciences,China University of Mining & Technology,Xuzhou 221116,China;2.School of Management,China University of Mining & Technology,Xuzhou 221116,China)
This paper introduces the study on the existence and uniqueness of solutions for fractional boundary value problems for a fractional differential equations of p-Laplacian operator by applying Banach contraction principle,given certain conditions,offers the sufficient conditions for the existence and uniqueness of solutions,and ends with several examples given to illustrate the results.
fractional differential equations;p-Laplacian operator;Banach contraction principle
O175.8
A
1671-0118(2012)05-0537-08
2012-04-17
国家自然科学基金项目(10771212)
张 宁(1985-),女,山西省晋城人,硕士,研究方向:微分方程边值问题,E-mail:ninging-love@163.com。
(编辑 王 冬)
———理学院

