向列相液晶中相位光栅光束耦合特性

任常愚， 丁红伟， 尹向宝， 程俊廷

(1.黑龙江科技学院 理学院，哈尔滨 150027;2.黑龙江科技学院 现代制造工程中心，哈尔滨 150027)

向列相液晶中相位光栅光束耦合特性

任常愚1， 丁红伟1， 尹向宝1， 程俊廷2

(1.黑龙江科技学院 理学院，哈尔滨 150027;2.黑龙江科技学院 现代制造工程中心，哈尔滨 150027)

为了研究向列相液晶中相位光栅光束耦合特性，从理论上分析了相位光栅的光束耦合和衍射规律，采用掺杂C60垂直排列的向列相液晶(5CB)，厚度为20 μm的样品，进行二波耦合(TBC)实验，研究动态衍射和光束放大特性。结果表明:相位光栅的衍射强度分布呈现明显不对称。根据取向光折变效应表面电荷调制机制和电场作用下的Carr-Helfrich效应对此现象给出定性解释，认为非对称光强分布来自于样品中产生的非对称相位光栅。液晶中非正弦调制的空间电荷场产生了非对称相位光栅。

非线性光学;向列相液晶;相位光栅;光束耦合

0 引言

向列相液晶(Nematic Liquid Crystals，NLCs)是一种非常重要的光折变(Photorefractive，PR)材料。它可以在较大的角度范围和较宽的波长区间，以及很低的外加电场(～0.1 V/μm)和较低的光功率(～mW)下，利用光折变效应记录相位光栅。Rudenko和 Khoo等［1－4］在 1994 年首次报道向列相液晶中的取向光折变效应后，立即引起了研究者的极大兴趣。由于此效应可使两束相干光在向列相液晶写入动态相位光栅，因此，向列相液晶在数据存储、图像识别、光学滤波、传感器保护装置等［5－6］光子学领域具有广泛的应用前景。

据传统的光折变理论，NLCs中形成的全息光栅为纯位相薄光栅，光栅函数(折射率调制函数)为对称函数，且满足Raman-Nath衍射。该光栅衍射时有多阶衍射现象，且高阶衍射强度呈对称分布。

笔者团队的实验发现，制备的NLCs样品中形成全息光折变光栅的衍射具有显著的不对称性，产生了明显的光束耦合现象。解释这种现象的完整理论分析目前尚未见诸文献，笔者利用标量衍射理论分析薄光栅的衍射及光束能量耦合特性，并对光栅形貌特征进行分析，研究非对称光栅形成的物理机制。从实验中探讨C60掺杂向列相液晶薄膜中记录的全息光折变光栅动态光束耦合与外加电压的关系。

1 实验样品及光路

实验所用样品是Sigma-Aldrich公司生产的向列相液晶5CB(4，4-n-pentylcyanobiphenyl)，掺杂了质量分数约为0.05%的富勒烯C60，制成垂直排列厚度为20 μm的液晶盒。C60会被光激发而产生光致空间电荷，具有增强光导电性的作用，从而增强液晶中的空间电荷场［7］。其结果是使NLCs具有更强的光学非线性，增大样品中形成光栅的衍射效率。

图1是典型的二波耦合(Two Beam Coupling，TBC)实验光路。光源为 He－Ne激光器发出的632.8 nm的水平偏振(p-polarized)的线偏振光，分束镜(BS)将入射光束分为两束相干的记录光I10和I20，二者以θ≈1.5°的夹角相交于液晶盒上，从而在液晶薄膜中形成光折变全息光栅的光栅间距Λ，Λ =λ/2n0sin(θ/2)，约为29 μm，n0为液晶的平均折射率，所使用的液晶薄膜的厚度d≈20 μm，样品的法线与两束记录光的角平分线的夹角β≈45°，通过直流电源把直流电压施加到两个ITO电极上，从而在液晶薄膜中产生直流电场。当样品倾斜放置时，衍射不对称，规定偏向液晶盒法线方向的衍射为正(I+1，I+2，…)，另一方向为负(I－1，I－2，…)。I12和I21分别为I10和I20的透射光。

文献［8］给出的量纲 1 参数 Q=2πLλ/n0Λ2，其中，L=d/cos β，是判别光栅特性的一个重要指标。对于薄光栅(Thin gratings)，Q＜＜1;对于厚光栅(Thick gratings)，Q＞＞1。在图1给出的实验配置下有 Q=2πLλ/n0Λ2≈0.07 ＜＜1，说明 NLCs中记录的光栅为薄光栅。在这种情况下，二波耦合实验中将出现Raman-Nath多阶衍射现象。固定两束632.8 nm的记录光为p偏振的线偏振光，功率均为I10=I20=4.7 mW。二者在样品处的光斑直径约为2.0 mm。

图1 二波耦合实验示意Fig.1 Schematic of two wave-coupling experiments

在二波耦合过程中，两束相干的p偏振光之间存在明显的自衍射现象和非对称能量转移现象;而两束相干的s(s-spolarized)偏振光之间不存在耦合行为，也不会产生自衍射现象。但是，无论是p偏振还是s偏振的写入光都能够在NLCs中记录光栅，而只有p偏振的光才能被光栅衍射。另外，没有外加电压时不能记录光栅。这些实验说明液晶薄膜中记录的光栅来源于外加电场和空间电荷场共同作用下液晶分子的重新取向，即该光栅为光折变全息光栅。

2 相位光栅光束耦合的理论分析

在光折变介质中记录的光折变全息光栅能够使两束记录光在经由光栅时一束光被放大，另一束光被衰减，从而出现非对称能量转移现象，即二波耦合(TBC)现象。光折变效应的很多重要应用都依赖于二波耦合中的非对称能量交换。

考虑两束相干记录光入射到光折变介质中，其光电场形式如下［9］:

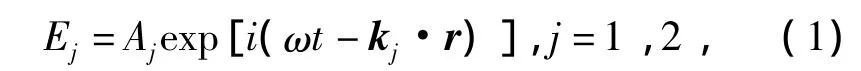
式(1)中，Aj为光波振幅，ω为角频率，kj为波矢。此干涉光照射到介质上形成干涉条纹，光强分布为

式(2)中，K=k2－k1为光栅波矢，满足Bragg条件，大小为2π/Λ。由光折变效应 (Pockels effect)可知，入射光场诱导介质折射率周期分布可写成［9］

式(3)中，c·c·表示复共轭;在不考虑吸收的条件下，I0=I1+I2=|A1|2+|A2|2;n0为光照之前介质平均折射率;Δn为光折变效应产生的折射率改变量，大小与材料特性、光栅间距，以及材料的导轴及电光系数有关;φ为光折变效应中折射率空间分布与光干涉图样的相位之差，只考虑扩散机制情形下φ=π/2。为了研究介质中波的耦合行为，假设入射光在x－z平面传播，如图2所示。

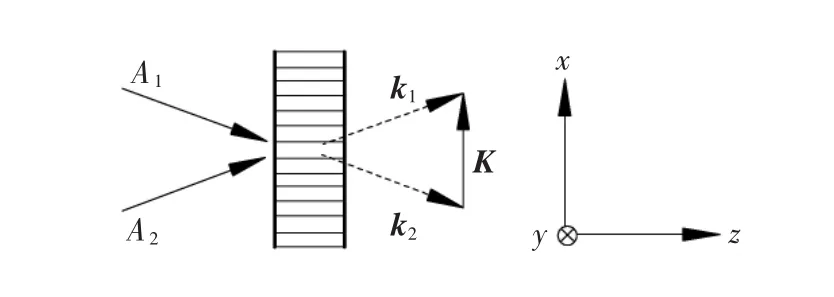
图2 同向入射的二波耦合Fig.2 Co-directional two-beam coupling

为简化问题，设在x方向相位光栅无限大，并只考虑两波在z轴方向上的变化。将式(1)和(3)代入波动方程，有

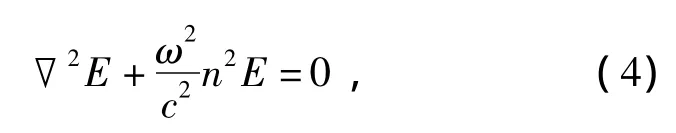
式(4)中，c为光速，n为介质折射率。

利用振幅缓变近似条件(The slowly varying amplitude approximation)

2θ为入射光在介质中夹角，且对称入射。能量耦合方向由β1和β2之间符号确定。

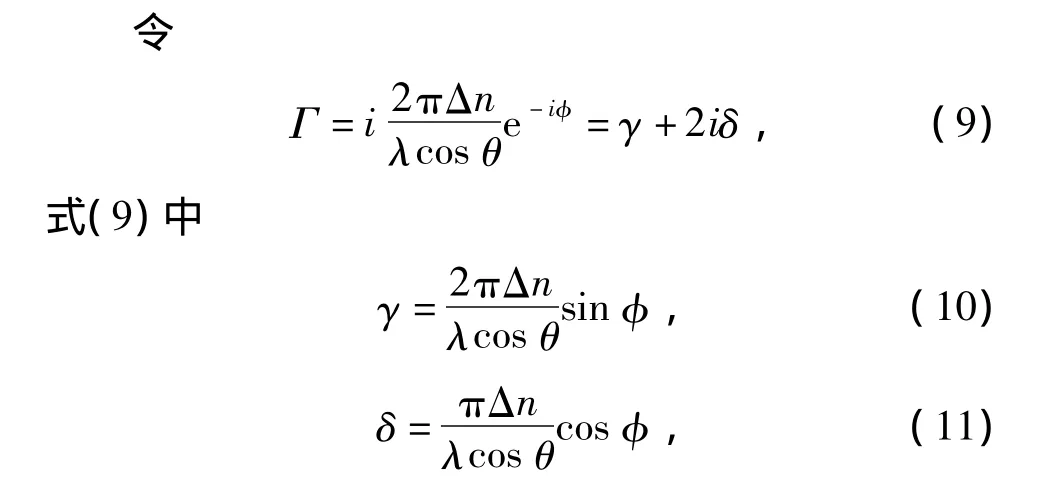
Γ为复数耦合常数(The complex coupling constant)，φ为光折变全息光栅相对于干涉条纹的相移。在不考虑吸收的条件下(α=0)，两束记录光在光折变全息光栅中相互耦合的表达式［10］为:

式(12)和式(13)中，z为入射面内光栅波矢的垂直方向;I10、I20分别为记录光刚入射样品时对应的光强;m=I10/I20为调制度;在相移φ不等于零的情况下，即光栅为非局域光折变全息光栅，一束记录光的强度随着耦合距离的增加被单调地放大，另一束记录光的强度被单调地衰减。γ越大，两入射光能量耦合越强。由式(9)可知，当 Δn固定，相位 φ=±π/2时，γ最大，表示衍射光I12和I21之间有最大能量转移。

在NLCs光折变效应中，由泊松方程▽·Esc=ρ/ε可知，折射率相位光栅与强度光栅之间的相移接近π/2，相位光栅是一种非局域光栅。对二光束耦合起决定作用的两个因素，一是折射率相位光栅对于空间干涉条纹的相移(φ)，另一个是折射率改变量(Δn)，而空间相移的大小［9］则为

式(14)中，Ea是外加电场，ED是扩散电场，Esc是空间电荷场。由此可见，外加电场的大小和方向将影响空间相移的取值，也就是说两光束之间的能量耦合与外加电场有关。

3 能量耦合及高阶动态衍射特性

在图1所示的实验配置条件下，利用坐标记录纸记录了外加电压分别为正向和反向时，二波耦合两束透射光I12和I21的能量耦合特性，如图3所示。

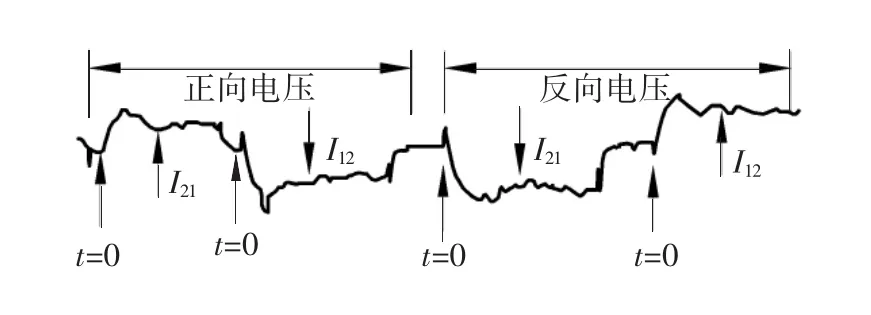
图3 二波耦合动态响应曲线与电压极性的关系Fig.3 Dynamics of two-beam coupling under application of dc voltage with polarity opposite

由图3可以看出，一束透射光强增强，另一束必然减弱，与表达式(12)、(13)预期结果基本一致。电压反向时，相当于空间相移φ符号改变，能量耦合方向也改变。

为了进一步了解NLCs薄膜中记录光栅的衍射特性，在图1所示的实验配置和电压极性下，固定两束记录光的功率均为4.7 mW(光斑直径为2.0 mm)，利用CCD拍摄了增加外加电压的过程中记录光经由薄膜中记录的光栅衍射后产生的可测的动态自衍射强度分布，并用Origin绘图软件绘出不同电压时各阶衍射光强的分布曲线，如图4所示。

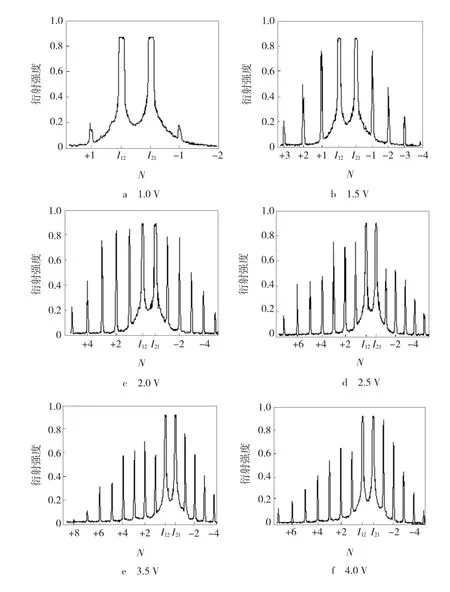
图4 衍射强度随电压的变化Fig.4 Dynamics of tdiffraction intensity of all orders at different applied voltages

由图4可以看出，衍射强度分布具有以下特点:(1)电压较小时，透射光两侧的衍射光强基本呈现对称分布。(2)电压增加到2.0 V时，透射光两侧的衍射光强出现非对称的现象，即I+i≠I－i，透射光两侧相应衍射阶(N)的衍射效率是不对称的，随着电压的增大非对称分布愈加明显，既表现在衍射阶数，又表现在衍射强度上;在电压小于3.5 V，正的(+1，+2，…)衍射强度和阶数都要优于负的(－1，－2，…)衍射。(3)当电压达到4.0 V 时，虽然正的衍射阶数要多于负的，但衍射强度却出现了相反的情况。(4)在电压变化的整个过程中，两束透射光的强度是随时间在变化的，但在稳定情况下并未见到明显的差别。

如果实验条件不变，只改变电压极性，则衍射强度分布随外加电压增加的演化过程与图4中相似，只是第+i阶衍射随着外加电压的演化特性变成图4中的－i阶。即外加电压的极性决定是+1阶，还是－1阶的衍射效率能够达到最大，以及光斑不对称的分布形式。

［8］的报道，如果描述折射率调制的函数为对称函数时，即其可以表示成偶函数形式时，高阶衍射强度分布呈对称形式，有η+i=η－i(i=1，2，…)。然而，对于非对称位相薄光栅而言，描述该光栅的折射率调制的函数不可以表示成偶函数形式。因而，为了解释上述实验现象，笔者认为在NLCs薄膜中光栅能量耦合分布的不对称极有可能来源于光栅调制形式的不对称，从而导致衍射强度的不对称，并使得衍射能量不对称分布于透射光的一侧，呈非对称分布形式。

对于NLCs中具有非对称函数形式的取向光折变全息光栅而言，光栅的记录来源于光致界面电荷的调制，并被Carr-Helfrich效应放大。另外，两个电极所具有的不同的载流子注入势垒将会使得界面吸附电荷的调制度不同，Carr-Helfrich效应产生的空间电荷场EΔσ和 EΔε也非正弦形式［11－14］。这些因素极有可能使得液晶薄膜中产生的折射率调制接近于如锯齿形的非对称函数形式，使得光栅衍射为非对称形式。

4 结束语

在NLCs系统中，光折变效应所形成的光栅为非局域光栅，采用光折变光栅下的耦合波理论近似地描述液晶中薄光栅的耦合特性，给出了两束光强耦合过程中能量耦合的动态演化规律，二波耦合实验证实了非对称能量转移的存在。

在不同外加电压下存在三种不同类型的耦合情况，其特点是:被衰减的透射光的强度变化规律基本相同，即衰减开始时会出现一个小的脉冲增强，然后光强度迅速减弱，随着记录时间的增加下降速率越来越缓慢，最后趋于稳定。对于放大的信号光则有三种情形，一是信号光光强开始增大，最后基本上达到稳定值;二是信号光的耦合达到最大之后稍有减弱，但只要电压存在就可维持在一个稳定的水平上;三是信号光的耦合达到最大后，迅速下降，很快便下降到不加外加电压时该光束通过样品后的透射光强度，之后其强度还将继续下降，且下降的幅度比初始增加的幅度还要大。

目前，尚未从多波耦合方程得到薄光栅情况下的简单的解析解。笔者从实验角度研究了相位光栅的动态衍射特性，以及高阶衍射强度非对称性随外加电压的关系。

参考文献：

［1］KHOO I C.Liquid crystals:physical properties and nonlinear optical phenomena［M］.New York:Wiley and Sons，1995:1 －19.

［2］RUDENKO E V，SUKHOV A V.Optically induced spatial charge separation in a nematic and the resultant orientational nonlinearity［J］.JETP，1994，78(6):875－882.

轴距(mm) .................................................................2453

［3］KHOO I C.Orientational photorefractive effects in nematic liquid crystal films［J］.IEEE J Quantum Electron，1996，32(3):525－534.

［4］WIEDERRECHT G P.Photorefractive liquid crystals［J］.Ann Rev Mater Res，2001，31:139 －169.

［5］任常愚，孙秀冬.向列相液晶动态全息存储特性的研究［J］.光子学报，2005，34(5):785－788.

［6］LEE W，WANG Y L.Evidence for holographic image storage in a fullerene-doped liquid-crystal film［J］.Chin J Phys，2001，39(4):295－298.

［7］WANG Y.Photoconductivity of fullerene-doped polymers［J］.Nature，1992，356(6370):585－587.

［9］YEH P.Introduction to photorefractive nonlinear optics［M］.New York:John Wiley＆ Sons Inc，1993:309－390.

［10］WIEDERRECHT G P.Photorefractive bragg gratings in nematic liquid crystals aligned by a magnetic field［J］.Appl Phys Lett，1999，74(23):3459－3461.

［11］任常愚，蔡吉花，金永君，等.掺杂C60向列相液晶全息光栅衍射增强的研究［J］.光学学报，2011，31(2):166－172.

［12］SUN X D，REN C Y，PEI Y B，et al.Electrically controlled dynamic holographic gratings in fullerene C60-doped nematic liquid crystals［J］.Journal of Physics D:Applied Physics，2008(41):245105.

［13］ZHANG J，OSTROVERKHOV V，SINGER K D，et al.Electrically controlled surface diffraction gratings in nematic liquid crystals［J］.Opt Lett，2000，25(6):414 －416.

［14］PAG LIUSI P，CIPPARRONE G.Surface-induced photorefractive-like effect in pure liquid crystals［J］.Appl Phys Lett，2002，80(2):168－170.

Beam coupling of phase grating in nematic liquid crystals

REN Changyu1， DING Hongwei1， YIN Xiangbao1， CHENG Junting2
(1.Collegel of Sciences，Heilongjiang Institute of Science ＆ Technology，Harbin 150027，China;2.Modern Manufacture Engineering Center，Heilongjiang Institute of Science ＆ Technology，Harbin 150027，China)

Aimed at investigating the beam coupling characteristics of nematic liquid crystal phase grating，this paper offers a detailed theoretical analysis of beam coupling of phase grating and diffraction properties and describes the study on dynamic diffraction and beam amplification properties，drawing on the 20 μm-thick sample which is C60-doped homeotropically aligned nematic liquid crystals(5CB)and the two beam coupling(TBC).The results show the occurrence of evident asymmetry in the distribution of the diffractive intensities.The paper features a qualitative explanation for the occurrence，according to the light-induced surface-charge modulation mechanism and the Carr-Helfrich effect in the presence of an applied electric field and concludes that the asymmetric distribution is due to the asymmetric phase grating in the sample.The space-charge field of the non-sinusoidal modulation in liquid crystal leads to the asymmetric phase grating.

nonlinear optics;nematic liquid crystals;phase grating;beam coupling

O734

A

1671－0118(2012)01－0068－05

2011－12－06

黑龙江省自然科学基金项目(A200915);黑龙江省教育厅科学技术研究项目(12511493)

任常愚(1963－)，男，黑龙江省宁安人，教授，博士，研究方向:液晶材料与非线性光学，E-mail:renchangyu@126.com。

(编辑 徐 岩)