雷击引燃森林可燃物概率的实验研究
朱 易,刘乃安,邓志华,张林鹤
(中国科学技术大学火灾科学国家重点实验室,安徽 合肥,230026)
雷击引燃森林可燃物概率的实验研究
朱 易,刘乃安*,邓志华,张林鹤
(中国科学技术大学火灾科学国家重点实验室,安徽 合肥,230026)
利用自主设计的雷击点燃森林可燃物的模拟实验装置,采用大兴安岭地区的松针和白草作为实验材料进行了雷击点燃实验。通过Logistic回归分析得到雷击点燃概率方程,并且通过主成分分析发现可燃物含水率和设备的低压值是决定可燃物是否被点燃的主要因素。通过不同可燃物含水率和电极间距参数条件下的实验证明了Logistic回归方程结果的合理性,并对电极间距改变范围对实验的局限性进行了分析。
雷击火;最小电弧能;可燃物含水率;主成分分析;Logistic回归分析
0 引言
雷电是引起森林火灾的主要自然原因之一[1]。为降低雷击火对森林的破坏,需要对雷击火发生的机理进行深入研究。国内外对于雷击火发生机理的研究主要分为两类,一是从宏观角度,通过对卫星、气象信息和历史数据的处理,研究和揭示雷击火的时空分布规律;二是从微观的角度,对雷击火放电和在小尺度实验台模拟雷击火的发生,从而揭示雷击火发生、发展规律。美国Latham[2]最早研制出小尺度雷击火模拟实验平台,即是用电弧来模拟雷电,采用了当地森林可燃物(西黄松枯枝落叶、朽木等)作为实验材料,得到了不同可燃物的点燃概率Logistic方程。研究还发现当可燃物含水率低于40%时,点燃的概率随着含水率的增大而减小。Darveniza等人[3]也研制了雷击试验台,从能量角度进行研究,计算雷电点燃可燃物所需要的能量,实验证明了薄木板比厚木板被点燃的概率更大,长连续电流比脉冲电流更加容易点燃可燃物。
虽然前人已经研究了含水率、可燃物种类、可燃物厚度因素对点燃的影响,但考虑的参数条件有限,研究系统性不够,很难被应用到实际过程中。本实验通过自制的雷击点燃可燃物模拟实验装置开展实验研究,分析影响可燃物点燃的主要因素,并运用SPSS18.0软件对实验数据进行分析,描述温度、空气湿度、可燃物含水率等变量的作用,采用Logistic分析得到可燃物点燃概率方程并进行有效性分析。

图1 雷击点燃可燃物模拟实验设备Fig.1 Equipment for simulating the ignition of fuels by lightning
1 实验
1.1 实验设备
本文实验采用了自主研发的雷击火实验设备。设备实物如图1所示,原理如图2所示。是通过高压击穿和电弧低压放电来模拟雷击点燃可燃物。实验设备主要有以下五个部分构成:

图2 点燃部分的设备原理图Fig.2 Experimental schematic of ignition section
(1)高压端由铝钢材料制造,对频率为50Hz、电压220v的交流电进行整流滤波和四次加压,形成高电压,电压最高可以达百万伏量级,设备通过电容分压器降压进而对高压端的电压值进行测量。
在图2左侧部分所示的是冲击本体,通过整流滤波和脉冲功率滤波装置对交流电进行整流,得到实验所需要的电流,然后由控制台的控制部分对冲击本体或冲击电流发生器充放电。冲击本体可以产生0kV~1000kV,持续数十纳秒的脉冲。该脉冲可以击穿几厘米的空气和一定厚度的可燃物(本实验采用了木板,纸张、松针和白草),但其能量不足以点燃任何可燃物。
(2)低压端由一个恒流充电器、50个4800PF/630V电容和四个大电感组成,通过电感调节放电电流的持续时间,利用电容来储存电能。该装置通过电流发生器来产生单一的峰值较小的电流。恒流充电器输入为220V交流电,以220V直流恒流输出对电容列充电。当高压本体发生器触发产生一个高压短脉冲击穿陡波球隙G1后,a处电压会急速增高,高压为0kV~1000kV。随后高压击穿空气间隙时,冲击电流发生器中电容放电生成持续几十ms的电流,平均值约为150A,峰值约为300A。该电流用来点燃可燃物样品。在高压击穿G1后由于L的存在阻止了电容两端电压的升高,对电容列起到很好的保护作用。

(4)实验控制台由控制按钮、显示仪表和示波器等组成,可控制低压、高压充放电、开关和接地装置。显示仪表可以实时显示高低压端的电压值。示波器(Gwinstek GDS-3354 350MHz 5GS/s)可精确显示高压端的电压值和低压端的电流值。测量数据以图表形式进行储存。
(5)安全保护部分由自动接地杆和手动接地杆构成,接地杆通过地线释放设备的残余电流,避免触电事故的发生,保证了实验的安全性。另外试验台被放置在封闭环境中,排除自然风、温度、空气湿度等因素对可燃物点燃的影响,使实验尽可能在理想状态下进行,保证了实验的精确性。
1.2 实验材料
实验材料是采自大兴安岭地区的松针和白草。东北松针(枯萎)的含水率在10%左右,白草的含水率在5%~10%。松针或白草用切割机切成细末,不断加湿、烘干(通过恒温恒湿箱和烘干箱),得到达到含水率要求的实验样品(5%~50%)。不断加湿和烘干,一方面是使样品达到一定的含水率,另一方面是保证样品的水分均匀。
1.3 实验步骤
(1)打开并调试设备,并将按实验要求加工后的可燃物放置在测试台上;
(2)实验开始后,记录环境温度T、相对湿度H;用水分测定仪测量可燃物含水率,并测量可燃物体积密度ρb和堆放厚度δ;使用刻度尺测量两极间距d;
(3)对低压和高压充电,一般要充10s停一次(充电持续时间一般在30s~100s);
(4)对高压和低压同时进行放电;
(5)当电弧放电击穿空气并点燃可燃物便可认定点燃成功,将点燃概率记作1,反之为0(而空载时,当电弧放电击穿空气便可认定为点燃成功)。使用数字存储示波器记录冲击电压U(t)、初始低压值UL,最终低压值UL和高压UH,波形以图表形式进行存储;
(6)打开接地装置并关闭设备。
1.4 实验数据
实验观测的主要数据为可燃物在模拟雷击下的点燃概率P,为二分类变量,有0和1两个值,分别表示可燃物未被点燃和被点燃。实验中可改变的参数包括环境温度X1、相对空气湿度X2、高压端电压值X3、低压端电压值X4、两电极之间的间距X5和可燃物含水率X6。
X1:环境温度(℃)。通过空气调节装置对整个实验房间进行调节,变化范围为15℃~25℃。
X2:空气湿度(%RH)。通过空气调节装置调节,变化范围为35%RH~75%RH。
X3:高压端电压值(kV)。对高压端进行加压,调节范围在0kV~1000kV。
X4:低压端低压值(V)。对低压端进行加压,调节范围在0V~400V。
X5:电极间距(cm)。通过刻度尺进行调节,调节范围在0cm~5cm。超过5cm时可燃物很难被成功点燃。
X6:可燃物含水率(%)。实验样品的含水率为5%~50%。
2 主成分分析
由于本实验所涉及的各参数变量间可能具有一定的相关性,从而决定了变量所提供的信息会有所重叠。因此利用SPSS18.0软件对数据进行主成分分析[4],得到因子相关系数矩阵,作为提取因子的依据(表1)。

表1 因子相关系数矩阵Table 1 Correlation Matrix
从表2可以得出,主成分f1、f2、f3和f4的特征根都大于1。在主成分分析中,一般来说,主成分特征根大于1可以采用,小于1则意味着选择的指标不大合理或样本容量太大,采用这样的主成分解释力度太弱。结果看到,f1和f2的累计方差贡献率达到82.344%,因此只需选取这两个主成分进行分析。

表2 提取主成分因子的特征值及方差贡献率Table 2 Eigen values and contributing rates of primary factors
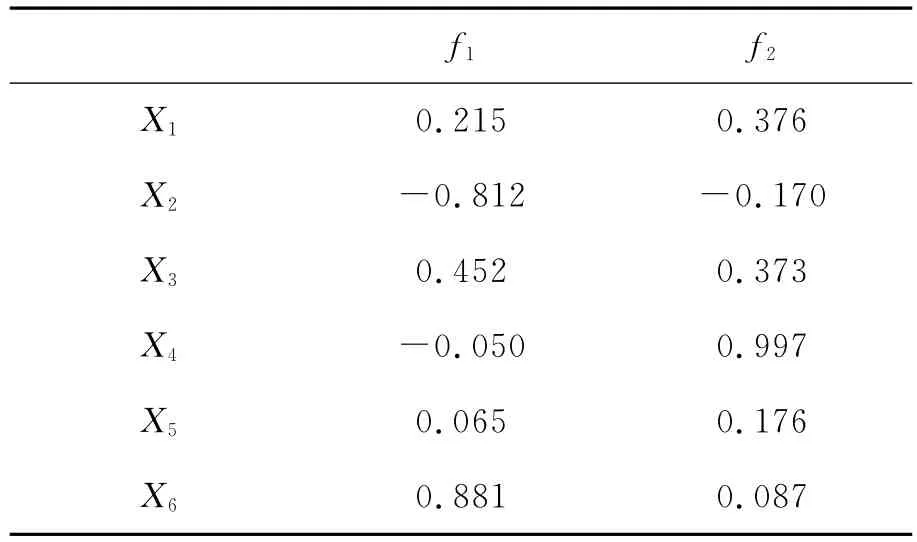
表3 旋转后成分矩阵(注:该变量为标准化之后数据)Table 3 The matrices rotated primary factor loadings
从表3可得:

由式(1)和(2)可见,第一主成分f1中的X2、X6的系数较大,表征可燃物和空气的水分对点燃的影响,其中X6即可燃物含水率的作用最显著;第二主成分f2中的X1、X3、X4的系数较大,表征外界能量和环境因素对点燃的影响,其中X4即低压值的作用最显著;而X5对于f1和f2的影响很小,可忽略。X5在统计分析中影响很小,这可能是由于电极间距变化范围太小所致。
3 点燃概率方程
Logistic回归分析是一种二分类因变量回归分析的方法,它是一种非线性的方法,多采用最大似然估计法。Logistic回归函数是一个累积分布函数,具有S型增长曲线。Latham[2]曾利用logistic分析得到以可燃物含水率为自变量的雷击点燃概率预测公式。
该模型包含实验中所使用的诸多变量,例如环境温度、电极间距、可燃物含水率等,变量可以是连续的,也可以是离散的。根据该模型,点燃概率与各影响因素的关系可表达为:其中Xi(i=1-m)为自变量,变化范围在(-∞,+∞),βi(i=1-m)为待估参数。

3.1 回归诊断
由于各因素之间可能具有相关性,使得有些因素和其他若干因素可能构成线性组合关系。因此首先对自变量进行共线性诊断[5]。结果方阵的6个特征根为λ1=0.188,λ2=0.688,λ3=0.343,λ4=0.996,λ5=0.035,λ6=0.784,条 件 指 数 为k≈5.335<30。因而自变量多重共线性程度很小。再对模型的异常点、强影响点进行诊断,结果发现正常。因此可以对数据直接进行Logistic分析。
3.2 最大似然比检验(χ2分析)

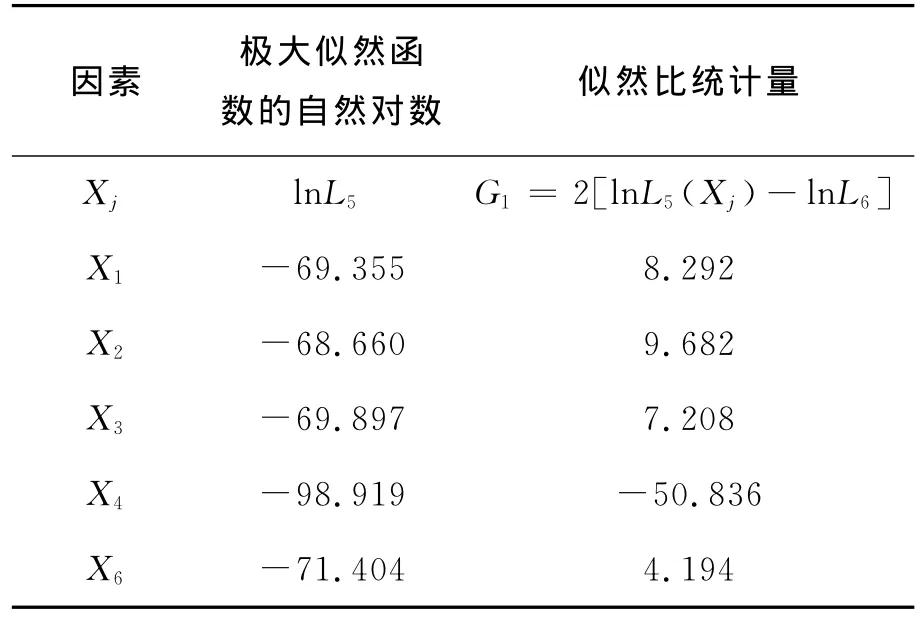
表4 似然比统计量Table 4 Statistical result of likehood
3.3 Logistic回归概率方程
通过极大似然法,将上述整理的实验数据进行计算,可得到回归系数β0,β1…,β5。通过编程计
皮尔逊χ2检验:
似然比统计量G1(Xj=2[lnL5(Xj)-lnL6])的中间变量lnL5(Xj)表示除了Xj的极大似然数函数的自然对数值,lnL6表示所有6个因子的极大似然函数的自然对数值(-73.501)。在大样本中,如算得到它们的回归系数:
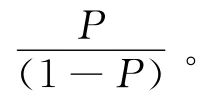
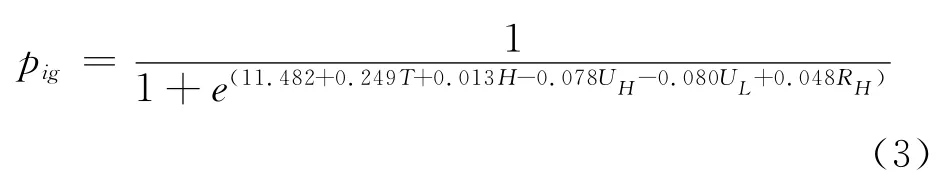
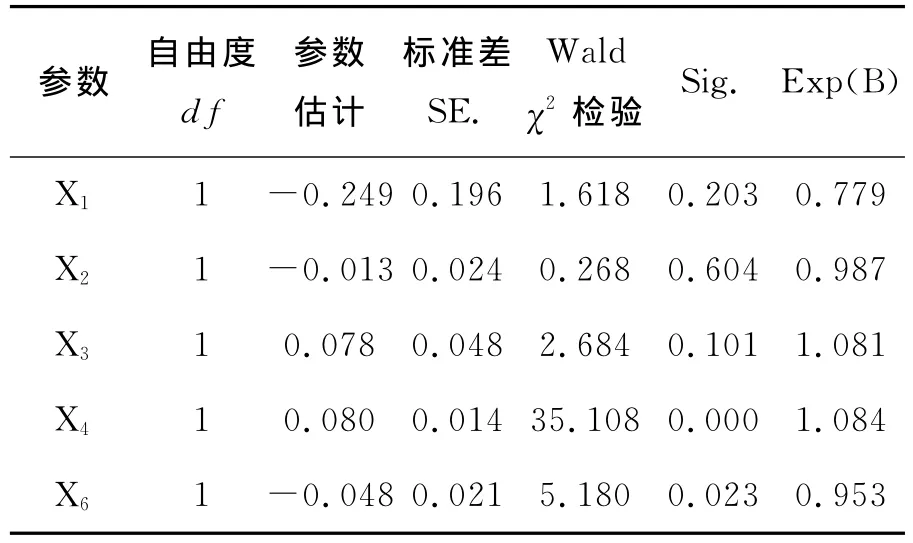
表5 参数估计Table 5 Parameter estimation
公式(3)表明当环境温度X1增大时,点燃的概率减小。温度对可燃物点燃的影响可表现于多方面。温度可以分为整体环境温度和可燃物表面温度,在实验条件下,两个温度是完全一致的。整体环境温度升高,空气中含有水分越多,使得可燃物的含水率也随之增大;而可燃物表面温度升高,则促使可燃物表面水分蒸发,使可燃物含水率相对减少。但根据文献[7],温度与可燃物含水率呈正相关性,可见在实际过程中整体环境温度的影响要大得多。当高压X3和低压值X4增大时,点燃概率随施加能量的增大而增大。当可燃物的含水率X6增大时,需要更多能量蒸发可燃物水分。此外,点燃概率随电极间距的增大而减小。
3.4 模型的有效性
(1)Hosmer-Lemeshow Test。
似然比函数的自然对数值对样品数目很敏感,作为补充和参照,需要 Hosmer-Lemeshow检验。该检验以卡方分布为标准,但一般要求其卡方值低于临界值。取显著性水平0.05,考虑到自由度数目df=8,得到卡方临界值为15.507。作为 Hosmer-Lemeshow检验的卡方值11.887<15.507,检验通过。Sig.值0.156大于0.05,由此也可判知通过Hosmer-Lemeshow检验。

表6 Hosmer-Lemeshow检验Table 6 Hosmer-Lemeshow Test
(2)ROC曲线评价法
为评估模型有效性,通常采用模拟拟合效果检验,一般用AUC值来检验ROC曲线。

表7 ROC曲线评价表Table7 Value of ROC curve

图3 低压值ROC曲线Fig.3 ROC curve of low voltage
当模型预测效果最佳时,ROC曲线应从左下角上升至顶部,并在水平变化段到达右上角,面积接近1。曲线下面积为0.697,95%置信区间为0.625~0.768,其大致可认为是模型能正确预测的概率。该检验结果说明模型预测效果一般。
例如对低压值进行估计,如图3所示,ROC曲线下面积为0.847,表明已具有较高的准确性。而有些因子(如含水率)的ROC面积较小,表明预测的准确性较低。

表8 ROC曲线的AUC值Table 8 AUC value of ROC curve
从表8来看空气湿度变量ROC分析效果不好,这可能是因为空气湿度的变化范围太小。除了空气湿度,高压值和可燃物含水率效果也不好。尽管在实验中采用了近10种可燃物含水率,但还是相对较少。因此要得到较为准确的概率方程,需要进一步用较多种类的可燃物开展变化参数范围更大、次数更多的实验。
4 验证性实验
为了验证计算所得Logistic回归方程的合理性,增加了以可燃物含水率为独立变量的实验,比较可燃物含水率对于点燃概率和最小电弧能的影响。功率是瞬时电压U (t)和瞬时电流I (t)的乘积,能量通过对功率进行积分∫UIdt得到。实验中所使用的样品的含水率在5%~50%。

图4 最小电弧能Emin与可燃物(松针)的含水率之间的关系Fig.4 Eminversus moisture in experiments
在测量出电流参量的基础上通过积分求得点燃所需的最小电弧能,可燃物含水率是通过水分测定仪测得的(注,一般在实验操作前后进行测量,不能设定要求精确的含水率,例如5%、10%等),Fuquay[8]等人认为点燃能量 Eig= RHOB(170+6.20FM)(FM指可燃物的含水率,RHOB指可燃物载荷),即点燃能量与含水率FM存在一定的线性关系,点燃能量随着可燃物含水率增大而增大。由图4可知最小电弧能Emin随着含水率增大而增大,由于电极间距不变,可以认为击穿空气的电弧能不变,那么直接用于点燃可燃物的电弧能也随着含水率增大而增大,这正好与Fuquay观点相符。实验分为两组,第1组实验结束之后立即进行第2组重复实验。实验所用可燃物(松针)密度在0.08g/cm3左右,可燃物的厚度为0.55cm。
由两组实验结果可见,当可燃物含水率越大,点燃所需的最小电弧能就越大,就意味在施加能量不变的条件下,被成功点燃的概率就越低,这与Logistic回归方程的趋势相符合。
5 电极间距改变范围对实验的局限性分析
以上Logistic回归分析中忽略了电极间距的影响。因此我们进行了大量改变电极间距的实验。


图5 最小电弧能Emin与电极间距d之间的关系Fig.5 Eminversus d in experiments
图5是在空载(即没有放置任何可燃物)的情况下的实验结果,电弧能主要是用于击穿空气通道(有可燃物的情况下,电弧能除了用于击穿空气还要点燃可燃物)。最小点燃能Emin随着电极间距d的增加而增大。间距增大,所需要击穿的空气通道就要越长,所需的能量就随之增大。在间距为1.6cm~2.6cm时,两次实验比较吻合,最小电弧能Emin都是随着电极间距d的增大而增大,但是在间距d为2.9cm时,两组实验的最小电弧能Emin突然降低,而在电极间距d为3.0cm时,最小电弧能Emin突然上升,这可能是因为在电极间距d比较大时,电弧不稳定所致。
由于实验设备性能的原因,不能将电极间距调节过大。在对实验的处理结果中发现,电极间距变化的影响在Logistic回归分析中被忽略,但是实验结果显示,电极间距对于最小电弧能和点燃概率还是有相当大的影响。在后续的实验中,需要对设备进行改进,使电极间距变化范围更大,提高Logistic回归分析结果准确性。
6 结论
本文利用自主设计的雷击点燃可燃物的模拟实验装置,通过改变环境温度、空气湿度、两极间距、可燃物含水率等条件,采用大兴安岭地区的松针和白草作为实验材料进行了大量雷击点燃实验。通过Logistic回归分析得到雷击作用下可燃物的点燃概率方程。通过主成分分析发现可燃物含水率和设备低压是雷击点燃的主要影响因素。通过以可燃物含水率为单一变量开展实验,证明含水率的影响与Logistic回归分析相符合,从而证明了实验的合理性。通过自变量为电极间距的实验,发现电极间距对点燃概率影响具有显著影响,说明了电极间距改变范围对实验的局限性。
[1]于建龙.我国大兴安岭地区森林雷击火发生的预测预报[D].合肥:中国科学技术大学,2010.
[2]Latham DJ,Schlieter JA.Ignition probabilities of wildland fuels based on simulated lightning discharges[R].US:Intermountain Research Station,1989.
[3]Darveniza M,Zhou Y.Lightning-initiated fires:Energy absorbed by fibrous materials from impulse current arcs[J].Journal of Geophysical Research,1994,99:10663-10670.
[4]张文彤.SPSS统计分析教程[M].北京:高等教育出版社,2003.
[5]侯锡铭,王伟杰,温广玉.用Logistic回归方法建立林火发生预报模型的研究[J].东北林业大学学报,1995,23(1):102-107.
[6]陈渭民.雷电学原理[M].北京:气象出版社,2006.
[7]居恩德.可燃物含水率与气象要素相关性的研究[J].森林防火,1993,36(1):17-21.
[8]Fuquay DM,Aughman RG,Latham DJ.A model for predicting lightning fire ignition in wildland fuels[R].US:Department of Agriculture,1979.
Experimental study on the probability of lightning induced ignition of forest fuels
ZHU Yi,LIU Nai-an,DENG Zhi-hua,ZHANG Lin-he
(State Key Laboratory of Fire Science,University of Science and Technology of China,Hefei 230026,China)
In this work,a new equipment was used to simulate the ignition of forest fuels induced by lightning.The samples of pine litter and white grass collected from Daxing’anling region were used for experiments.Based on the data obtained in this work,aprobability correlation was summarized by logistic regression analysis.Principal component analysis was also used to extract the major factors for ignition.The results showed that moisture and electrode spacing may greatly affect the probability of ignition.The reasonability of the logistic regression analysis was verified by experiments of which the moisture and electrode spacing were varied independently.Additionally,the limitation of the varying range of the electrode spacing used in this work was discussed.
Lightning-induced fires; Minimum arc energy; Moisture content;Principal component analysis;Logistic regression analysis
X954
A
1004-5309(2012)-0071-07
10.3969/j.issn.1004-5309.2012.02.04
2012-03-11;修改日期:2012-03-30
国家自然科学基金项目(51120165001和51076148)和国家十二五科技支撑项目课题(2011BAK07B01-02)
朱 易(1986-),安徽滁州人,中国科学技术大学火灾国家重点实验室硕士研究生,主要从事森林火灾方面的研究。
刘乃安,E-mail:liunai@ustc.edu.cn

