基于博弈论的南四湖流域生态补偿理论分析

闫中月，崔树强，邵 波

（1.山东师范大学 人口·资源与环境学院，山东 济南 250014；2.山东省科技发展战略研究所，山东 济南 250014）

基于博弈论的南四湖流域生态补偿理论分析

闫中月1，崔树强1，邵 波2

（1.山东师范大学 人口·资源与环境学院，山东 济南 250014；2.山东省科技发展战略研究所，山东 济南 250014）

采用博弈论的分析方法寻找南四湖流域生态补偿主客体的纳什均衡。在静态博弈模型和动态博弈模型得出两个截然不同的均衡:静态博弈的均衡是（不保护，不补偿），动态博弈的均衡是（保护，补偿）。在静态博弈中进行激励设计，提高补偿客体保护水资源的积极性，实现帕累托最优，应该立法，制定严格的惩罚标准；动态分析是建立在完全信息的基础上，由此要求政府建立良好的信誉，才能保证均衡的长久，从而达到保护南四湖流域生态环境的目的。

博弈论；生态补偿；南四湖流域；纳什均衡；帕累托最优

博弈论，又称对策论，是研究理性的决策主体之间发生冲突时的决策问题及均衡问题，也是研究理性的决策者之间冲突及合作的理论[1]。博弈逻辑中最重要、最基本的是纳什均衡，它是在其他参与人的策略选择既定的前提下，每个参与人都会选择自己的最优策略，所有参与人的最优策略组合[2]。本文以博弈论的相关理论为基础，对南四湖流域生态补偿进行分析，为相关决策部门提供一个合理的参考，确保南四湖流域内水质达到国家要求的标准，从而使得南水北调东线工程顺利进行。

南四湖是南水北调东线工程重要的调蓄枢纽[3]。自20世纪80年代以来，随着南四湖流域经济发展和城镇化速度的加快，南四湖出现了湖泊干涸，水质污染严重等问题[4]，难以达到南水北调要求流域内水质达到地表水Ⅲ类标准[5]，山东省政府和南四湖流域当地政府也采取了迁移渔民、退耕还湿、关转并停高污染企业等一系列的措施，来解决南四湖的水质污染问题[6]，目前已经取得了相当明显的成果。为了不让“调水”变为“输污”，保证清水长廊的长期运行，需要对利益相关者进行经济上的补偿，以激励保护水环境的行为。

1 研究区概况

南四湖地处江苏、山东两省的交界地区，由南阳湖、独山湖、昭阳湖、微山湖等4湖相连而得名，南北长126 km，东西宽5～25 km，周边长311 km，最大水面面积1 266 km2，总库容为47.3×108m3，占山东省淡水面积的45%。南四湖流域总流域面积为31 700 km2，包括山东、江苏、河南、安徽4省32个县（市、区）[7]。本文研究范围为南四湖流域山东境内所有区域，北起大汶河左岸，南至废黄河南堤，东以泰沂山脉的尼山为分水岭，西至黄河右堤，属于淮河流域泗河水系，流域面积约2.6万 km2，包括济宁市、枣庄市、菏泽市和宁阳县三市一县。截止到2009年末，流域内总人口为2 239.34万，人口分布不均匀，运河两岸及沿湖地区的人口密度大，黄河南岸和湖东区的人口密度小。南四湖湖区内，居住着大约7.6万渔民和7.5万半渔半农民。

2 南四湖流域生态补偿的博弈分析

生态补偿涉及到流域内的企业、失地农民、受损渔民等等。由于涉及到的补偿主客体的分散性和关系的复杂性，本文作两个假设:即由政府作为区域公共利益代表进行协商，他们之间的策略选择将影响到生态补偿能否进行，政府作为各自地方利益的代表，是从本地经济利益出发，通常不愿意主动承担补偿任务；而生态环境的保护者无论是企业还是个人，本文统一称作为保护者，他们都被当成理性人，追求个人利益的最大化[8]。

2.1 静态博弈分析

基于以上两个假设，从静态分析的角度出发，也即假设在策略选择时，一方并不知道另一方的选择情况时，同时作出决策，分析南四湖流域政府与生态环境保护者之间的博弈。为了分析方便，假设S代表政府对生态保护者的生态补偿额，C代表保护者所花费的成本，P代表保护环境整个收益，S>C>0，P>S>0。利用划线法，找出各博弈模型的纳什均衡。

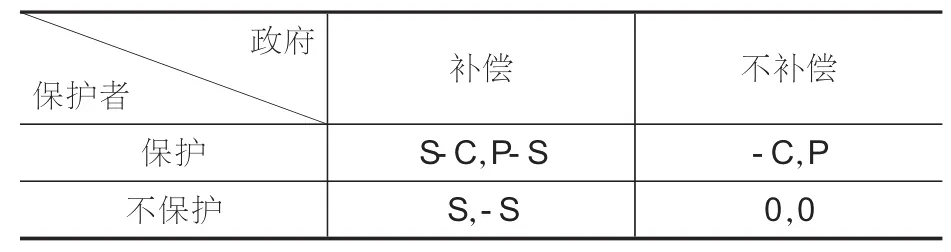
表1 保护者和政府间的博弈

此博弈模型的纳什均衡是（不保护，不补偿），此均衡不能实现帕累托最优。为了达到理想的均衡，先试着提高保护者的收益，得到下面的模型:

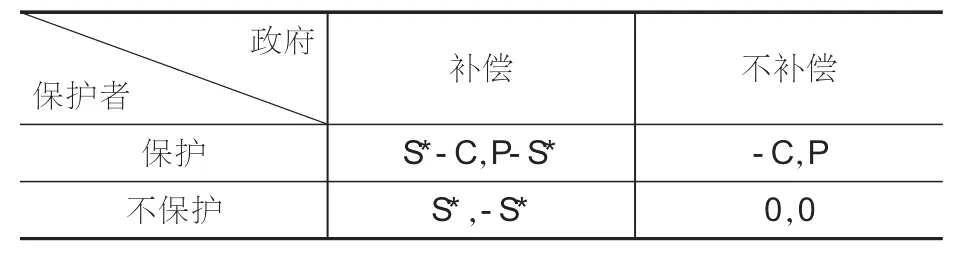
表2 提高保护者收益后的博弈

该模型的纳什均衡仍旧是（不保护，不补偿），博弈的均衡和没有提高保护者收益之前是一样的。如何打破这个困境，再次试着假定通过立法强制人们和企业去保护环境，如果不保护将会受到经济惩罚N，而如果其保护了环境，政府不补偿，保护者可以通过法律手段获得收益B，B是政府来提供。因此模型变为如下:

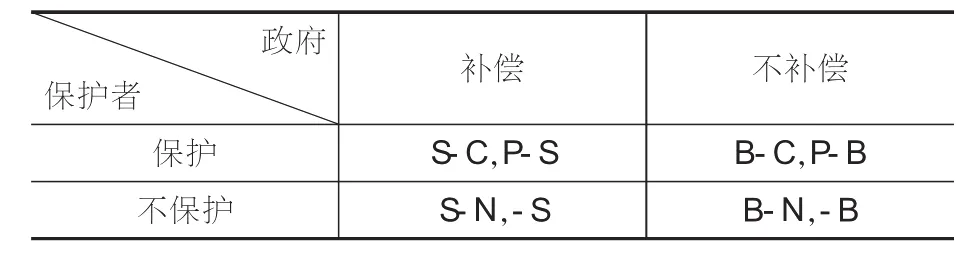
表3 加入罚金后保护者和政府之间的博弈

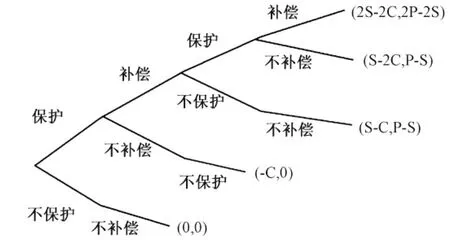
由于B和S、N和C的关系不确定，不能用划线法找出其纳什均衡。下面对其关系进行讨论。当B>S，N>C，即政府不补偿的损失大于其补偿的损失，保护者不保护的惩罚大于其保护所花费的成本，这个模型的纳什均衡是（保护，补偿），这是期待的结果；当BC，其纳什均衡是（保护，不补偿）；当B>S，N

通过分析可得:如果不补偿，保护者的最佳对策是不保护，提高保护者的收益，并不会改变博弈的均衡结果，而通过立法，确定一个合理的惩罚标准，且仅当B>S和N>C时的纳什均衡是期望的均衡结果。

2.2 动态博弈分析

基于以上两个假设，从动态分析的角度出发，即一方在知道另一方作出何种策略时再作出决策，假定政府与生态环境保护者之间进行多次博弈，当出现不补偿—不保护或不保护—不补偿时，博弈结束，否则博弈继续，其博弈树如图1。与以上假设一样每一次博弈，S代表政府对生态保护者的生态补偿额，C代表保护者所花费的成本，P代表保护环境整个收益，S>C>0，P>S>0。

图1 政府与保护者的动态博弈

利用逆向归纳法（backward induction） 得出此模型的纳什均衡是（保护，补偿）。与静态博弈分析的均衡结果不同，此均衡正是期望的结果。为什么静态博弈和动态博弈两种博弈模型会出现不同的均衡？可以看出两个博弈模型的前提假设是不同的，静态分析是一个非完全信息博弈，即双方在不知道对方选择策略的情况下，进行对自己有利的策略选择。动态分析是一个完全信息博弈，博弈双方选择策略时，知道自己所在的阶段，即在对方作出策略后，再选择策略。正是假设的不同，改变了博弈的均衡结果。也可以这么理解，静态分析中保护者对政府的补偿没有信心的，选择了不保护。而在动态分析中，保护者可以根据政府是否补偿，在下一阶段调整自己的策略，而政府也知道如果不补偿保护者，保护者在下一阶段将不再保护，保护者也知道政府知道如果不补偿保护者，保护者在下一阶段将不再保护，政府将选择补偿，所以保护者选择保护，以此类推，可以得出最终的结果是（保护，补偿）。

3 结论

在静态博弈分析中，如果不对双方的行为加以法律的限制，就会有一个坏的均衡（不保护，不补偿）。即没有人保护环境，没有人补偿。提高保护者收益是不会改变模型的结果，加入对保护者不保护和政府不补偿的惩罚，模型的纳什均衡则变为期望的（保护，补偿），其现实意义是通过立法确保保护者的利益和惩治违法违规行为，且设定保护者不保护的处罚N比其保护的成本C大，保护者保护环境时，政府不补偿所受的损失B，大于政府进行补偿的额度S，可以实现预期的结果。而在动态分析中，其纳什均衡是（保护，补偿），这一均衡的产生是建立在政府和保护者相互了解的基础上的，也就是说政府在此博弈中最重要的是要建立良好的信誉，树立起保护者对生态补偿的信心，以此达到保护与补偿的均衡。

[1]谢识予.经济博弈论[M].上海:复旦大学出版社，2002:30-37.

[2]张峰.论博弈逻辑的分析方法——纳什均衡分析法[J].北京理工大学学报:社会科学版，2008，10（ 2）:95-99.

[3]罗辉.南水北调改善南四湖水流水质特性及湖滨带控污技术研究[D].南京:河海大学，2006.

[4]梁春玲.南四湖湿地生态系统结构、功能与服务价值研究[D].济南:山东师范大学，2010.

[5]张先军，姚辉勇.南水北调东线南四湖人工湿地建设与规划[J].南水北调与湿地科技，2010， 8（ 3）:21-24.

[6]赵静.南水北调东线工程（南四湖一东平湖段）移民管理与实践[D].济南:山东大学，2009.

[7]张祖陆，沈吉，孙庆义，等.南四湖的形成及水环境演变[J].海洋与湖沼，2002，33（ 3）:314-321.

[8]杨明洪.退耕还林还草工程实施中经济利益补偿的博弈分析[J].云南社会科学，2004（ 6）:64-68.

The Theoretical Analysis on Ecological Com pensation based on the Game Theory in Nansi Lake Basin

Yan Zhongyue1,Cui Shuqiang1,Shao Bo2
（1.College of Population， Resources and Environment， Shandong Normal University，
Jinan Shandong 250014， China；
2.Shandong Institute for Development Strategy of Science and Technology，Jinan Shandong 250014， China）

This paper uses game theory to explore the Nash equilibrium for the subject and object sides of ecological compensation of Nansi Lake basin.There are two different equilibriums between static game model and dynamic game model:the equilibrium of static game is (no protection,no compensation),the equilibrium of dynamic game is (protection,compensation).In the static game,the incentives in order to improve the object's motivation to protect water resources and to achieve the Pareto optimal,related legislations are suggested to set up,which makes strict punishment standard,in order to achieve an expected equilibrium.The dynamic analysis is built on the basis of complete information,which requests the government to establish a good reputation in order to ensure a long-term equilibrium,so as to protect the ecological environment of Nansi Lake basin.

game analysis； ecological compensation； Nansi Lake basin； Nash equilibrium；Pareto optimal

X321

A

1008-813X（2012）01-0022-03

10.3969/j.issn.1008-813X.2012.01.007

2011-11-10

国家水体污染控制与治理科技重大专项淮河流域水污染治理技术研究与集成示范项目南水北调东线南四湖水质综合改善方案及支撑技术与示范课题（2009ZX07210-007）

闫中月（1987-），男，山东高唐人，山东师范大学人文地理学在读硕士研究生，主要从事区域人口研究。