应用BP神经网络预测高速铣削表面粗糙度

胡金平，高淑琴，齐立涛

（1.黑龙江科技学院 机械工程学院，哈尔滨 150027；2.平顶山平煤设计院有限公司，河南 平顶山 467000）

高速加工技术是一种以极大地提高加工的切削速度和进给速度,大幅度降低“切削工时”，从而提高机床生产效率的加工方法[1]。高速铣削的切削速度比传统铣削提高5～10倍，具有很好的表面粗糙度，表面粗糙度是高速铣削加工表面质量的一个重要评价指标，其主要影响因素之一是铣削用量的选则。因此，研究一种预测工件表面质量的理论模型，使其能够根据加工参数对产品质量作出预测，还可以确定满足零件表面粗糙度加工要求的工艺参数具有重要的意义。

1 实验条件

实验设备为Mikron HSM600U数控五轴高速加工中心，其控制系统为Heidenhain iTNC530，主轴最高转速42krpm，主轴功率13 KW，最大进给速度40m/min，定位精度0.008 mm。实验所用刀具为4齿硬质合金球铣刀，其直径10 mm，螺旋角30°，前角20°，后角8°。粗糙度检测仪为MITUTOYOSJ201p。工件材料为铝合金（2A70）。图1为实验系统示意图。表1实验的实测数据。

图1 实验系统示意图

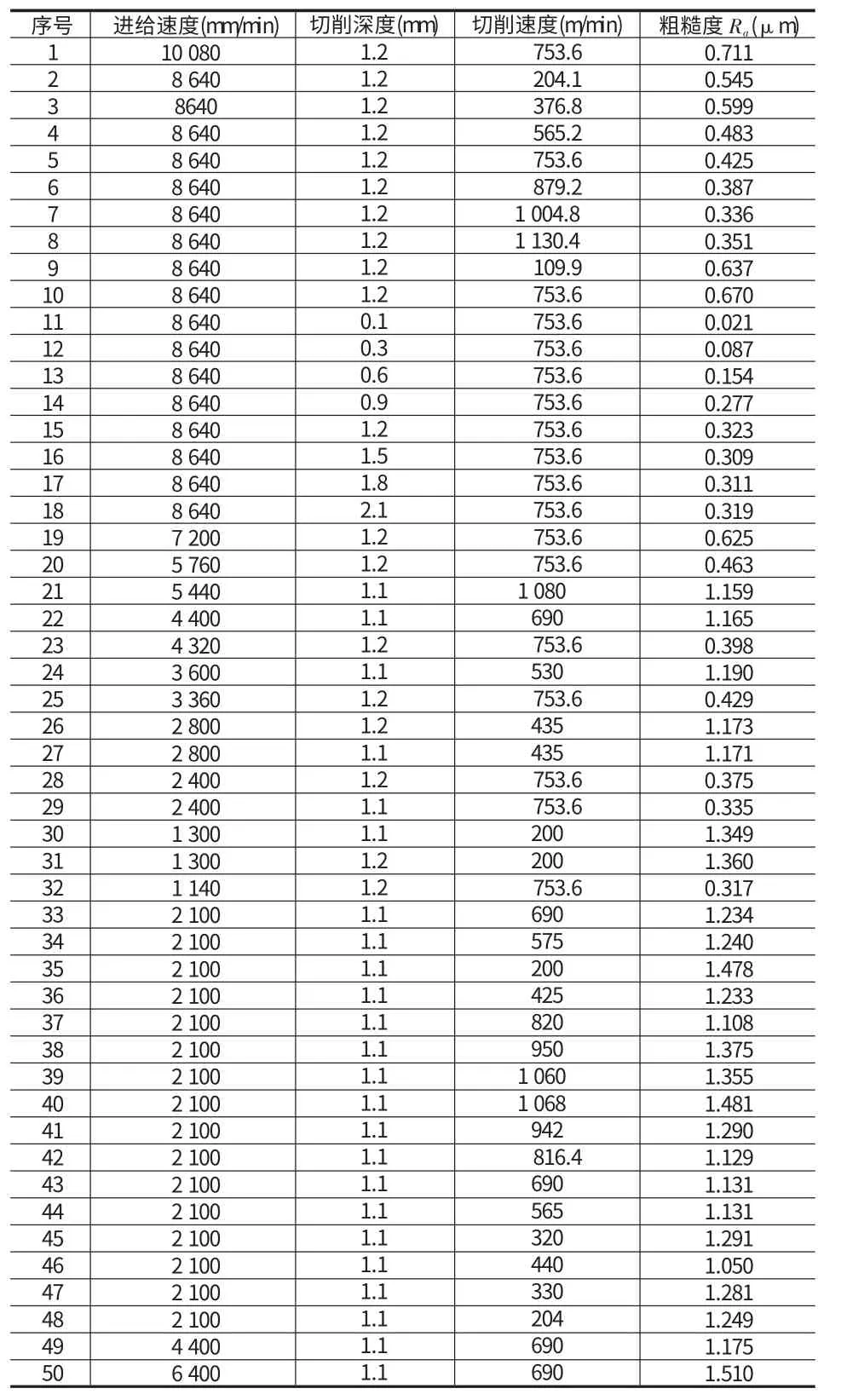
表1 训练模型的实测数据

2 BP神经网络

2.1 BP神经网络的基本原理

BP神经网络[2](Back propagation artificial neural network，BPANN)是目前应用最广泛的神经网络模型，它是一种按照误差逆传播算法训练的多层前馈型网络。BP神经网络能够学习和存贮大量的输入-输出模式映射关系，而且不需要事先揭示描述这种映射关系的数学方程，它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型包括输入层、隐含层和输出层，层与层之间多采用全部连接方式，同一层单元之间不存在相互连接。BP神经网络的节点作用函数通常为“S”型函数。

作用函数f（x）一般为可导的Singmoid函数：

误差函数R为：

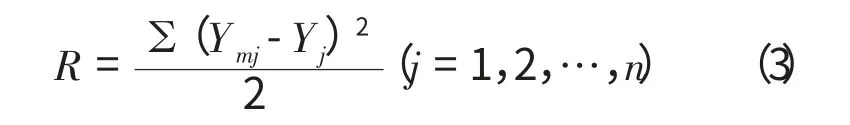
式中：Yj为期望输出；Ymj为实际输出；n为样本长度。

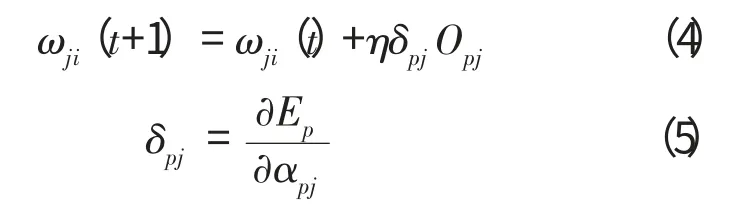
BP算法权值修正公式可表示为：式中：ωji为神经元的连接权值；η为网络学习率；Opj为样本的输出，δpj为误差修正值。

2.2 BP神经网络结构设计

在本文要建立的预测模型中，因为有3个自变量，1个因变量，所以确定该BP神经网络应具有3个输入层和1个输出层。BP神经网络结构的确定主要是要确定隐含层数和隐含层的节点数，因此，在建立多层神经网络模型时，适当的隐含层节点数的选取是非常重要的。经过反复的试算，最终确定该模型隐含层数为3，每个隐含层的节点数都是10，BP神经网络结构示意图如图2所示。

图2 BP神经网络结构示意图

2.3 BP神经网络学习训练

神经网络的学习主要是通过样本的反复训练来实现的，训练结果直接决定系统的质量。对本文的BP神经网络学习训练时，首先把原始的样本数据标准化，然后把最小训练速率设置为0.1，动态参数设置为0.5，Sigmoid函数设置为0.9，在训练过程控制中，最大迭代次数设置为10 000，允许误差设置为0.000 1。将表l中的第1组至第45组数据代入神经网络模型中进行训练。在训练过程中，当迭代次数达到10 000时，拟合残差如图3所示。

图3 网络训练残差曲线

当训练完成时，可以分别得到第l隐含层至第3隐含层各个节点和输出层各个节点的权重矩阵。将表1中的第46组数据至第50组数据作为检验数据，代入训练好的模型，得出如表2所示结果。

从以上研究可以看出，应用BP神经网络对表面粗糙度进行预测，其训练数据的预测值与实测值误差极小，在一定的试验条件下，检验用数据与实测数据的相对误差在1.323%至4.110%之间。误差的大小与样本的选取和收敛速度有关，要尽量选取具有代表性、涵盖全面的样本和既能完成学习过程，又要达到很好学习效果允许误差[3]。

表2 实测结果与预测结果的相对误差

3 结论

将人工神经网络技术引入铣削领域，应用BP神经网络建立了以进给速度，切削速度和切削深度为切削参数的高速铣削加工表面粗糙度预测模型。

预测值与实测值接近，能够得到较高的预测精度[4]，根据工艺参数对表面粗糙度做出预测，使加工人员能够准确掌握工件加工质量，对高速铣削参数的选择和表面质量的控制具有指导意义，有利于优化切削参数，从而提高企业制造自动化水平。

[1]胡金平.超高速铣削表面特征的研究[J].机械设计与制造,2006，183(5)：93-94.

[2]蒋建平，章杨松，阎长虹，高广运.BP神经网络在地基土压缩指数预测中的应用[J].中南大学学报(自然科学版)，2010，41(2)：722-727.

[3]黄旭钊，梁月明，李桐林.基于BP神经网络的航空物探数据分类方法[J].物探与化探，2010，34(4)：485-488.

[4]王 凯.铣削加工表面粗糙度的智能预测[J].机床与液压，2009，37(10)：58-59，119.