渗流场和应力场耦合应力变形数值分析
郝春华,龚 霞
(1.重庆市交通规划勘察设计院,重庆 401121 ;2.林同棪国际工程咨询(中国)有限公司,重庆 401121)
1 前 言
众所周知,在土石坝的施工过程中,不论土石坝如何被压实,在施工期间及初期蓄水时,总是要发生沉降变形的,因此控制好坝体的沉降是至关重要的,尤其是在施工和蓄水同时进行的情况下坝体的沉降变化对坝体的安全具有很大影响。目前渗流场和应力场耦合分析越来越受到关注,两者是不可分割的,将两者联系起来分析,能更好地反映出在坝体填筑过程中应力、应变的动态演化。
渗流场和应力场的耦合分析在裂隙岩体中早已成为热点问题,目前,己有较多的研究成果。对于土体而言,最有代表性的是基于Biot固结理论的渗流与应力的耦合模型。但该模型无论是以各向同性土体作为分析对象,还是以各向异性饱和软土作为分析对象,分析原理都是注重研究外荷载下孔隙水压力与有效应力(或总应力)及相应的变形之间的关系。这种分析方法其实与渗透力作用无关,所探讨的渗流场实质是孔隙水压力分布场,并不是渗流作用下所形成的渗透力场。也有学者采用耦合分析理论探讨渗流作用下渗流场与应力场的相互影响,但研究成果或是针对连续介质(岩体)的渗流行为建立数学模型 ,或是针对均质土坝建立耦合模型 ,较少分析非均质土坝的渗流场与应力场相互作用对土坝整体稳定性和局部稳定性的影响[1]。
本文结合覆盖层上的非均质心墙坝 ,采用耦合分析方法探讨在渗流场与应力场的作用下,大坝应力、应变的变化。
2 耦合模型[2-3]
2.1 土体平衡方程
Fredlund和Rahardjo曾对非饱和土壤介质的土体二维本构模型进行过描述,建立了土体本构关系。相应地,对于饱和区,孔隙气压等于大气压,水体充满介质孔隙,可以建立如下本构关系:
{Δσ}=[D]{Δε}+{m}Δuw
(1)
式中 [D]——线弹性矩阵,与弹性模量及泊松比有关;
{m}——各向同性单位张量;
Δuw——孔隙水压力增量。
据虚位移原理,将式(1)离散,可得如下形式:
∑[B]T[D][B]{Δδ}+∑{m}〈N〉{Δuw}=∑F
(2)
设[K]=[B]T[D][B],[Ld]={m}〈N〉,
简写之,即为:
[K]{Δδ}[Ld]+[Ld]{Δuw}={ΔF}
(3)
式中 [K]——劲度矩阵;
[Ld]——耦合矩阵。
2.2 渗流连续性方程
根据研究区岩土体渗流的特点,可以将其概化为非均质各向同性渗流模型。根据达西定律,可以建立如下渗流方程:
(4)
式中k(x,y)——不同渗流分区的渗透系数;
γw——水的容重;
θw——体积含水量,对于饱和区,体积含水量的变化量即为体应变(Δεv)的变化量。
据虚位移原理,式(4)可化为:
(5)
式中Vn——边界通量。
对上式进行有限元离散,可得:
(6)


[B]——应变矩阵;
[Kw]——渗流矩阵。
对渗流方程从t时间到t+Δt时间进行积分:
(7)
引入时间步因子θ,对式(6)应用时间差分得:
(8)
为了得到只包含孔隙水压力增量的表达式,对式(7)进行变形可得:
(9)
式中 {Q}——边界节点的流量。
联立式(3)、(9),即为描述应力场和渗流场的耦合方程。
由此可见,每一个节点都建立了三个方程,其中两个为平衡方程,另一个为水流连续性方程。静力变形分析模块的全局变量为应变增量,渗流分析模块中的全局变量为孔隙水压力增量。在耦合分析中,孔隙水压力的计算由渗流分析模块完成,而后将每一时段不同的孔隙水压力变化作为一种节点荷载赋予到静力变形分析模块中,在静力变形分析模块中计算每一时段土体中应力应变的变化。在渗流场与应力场的耦合过程中,应力应变与孔隙水压力是同步求解的。
3 计算实例分析
计算模型选取大坝的最大横剖面(见图1),坝顶高程2 510.00m,坝基高程为2 196.00m,灌浆帷幕底高程为2 100.00m。考虑大坝受力和变形的实际情况,采用位移约束条件。将地基底面设为x、y两个方向约束,地基顺河谷方向的两个端面设置x方向约束、y方向自由,即地基只能发生自由下沉。坝体部分均不设置约束,即坝体既可以产生x方向的位移,也可以产生y方向的位移。计算时主要考虑坝体填筑的施工步骤,认为地基变形已经完成,地基自重产生的应力场作为初始应力场。

图1 坝体最大横剖面
3.1 坝料的本构模型及参数
混凝土在本次研究中作为线弹性材料考虑。基岩由于是岩性条件很好的花岗岩,也作为线弹性材料考虑。上游围堰偏上游区和下游围堰下面的混凝土防渗墙与地基覆盖层之间可能存在较大的相对位移,为模拟覆盖层和混凝土之间的可能滑动,设置了接触单元。坝体的其它土料均采用邓肯—张E-μ模型,计算参数见表1。材料渗透系数见表2。基岩和混凝土的计算参数见表3。
3.2 计算方案及计算成果分析
本次计算仍采用分24层进行填筑,即坝体填筑到高程2 510m。每层填筑时间为100天,施工填筑共2 400天。填筑到位后开始进行蓄水,蓄水期为600天,蓄水至2 480m高程。
3.2.1 竖向位移计算结果及分析
图2~5为施工完成后开始进行蓄水的竖向位移等值线图。由图可知,从开始蓄水到蓄水结束,竖向位移的最大值逐渐减小,但减小的幅度不大,由4.219m逐渐减小到4.007m。减小的原因与孔隙水压力有关,在孔隙水压力的作用下坝体竖向位移会产生向上的位移,但位移变化不大。最大位移的位置由距坝底1/3心墙处有向斜上方偏移的趋势,但偏移趋势不是很明显。
3.2.2 水平位移计算结果及分析
图6~9为施工完成后开始进行蓄水的水平位移等值线图。由图可见,从开始蓄水到蓄水结束上下游的水平位移都有变化,上游最大位移由0.999m逐渐减小到0.653m,下游最大位移由0.489m逐渐增大到1.021m。对于水平位移,上游处水平位移逐渐较小,下游处水平位移逐渐增大。这是因为孔隙水的渗透作用下产生的,在渗透力的作用下坝体水平方向发生移动。

表1 邓肯-张E-μ模型计算参数

表2 计算材料渗透系数

表3 基岩和混凝土计算参数
3.2.3 应力计算结果及分析
图10~13为施工完成后开始进行蓄水的大主应力等值线分布图,图14~17为施工完成后开始进行蓄水的小主应力等值线分布图。由图可见,蓄水后大主应力变化不大,应力分布也没有较大改变;小主应力变化和分布有较大变化并且随着水位的不断增高小主应力逐渐减小。坝体两边由基本对称逐渐过渡为不对称。随着水位的不断提高,孔隙水压力逐渐增大,有效应力逐渐减小。
4 结 论
从上述计算结果分析来看,在数值模拟计算中,采用耦合分析对坝体沉降量的影响主要表现为以下两点;
(1)坝体的变形,在蓄水过程中最大竖向位移有减小的趋势,减小了0.212m,减小幅度并不大。上游水平位移也逐渐减小,减小了0.346m;下游水平位移逐渐增加,增加了0.523m,增大较为明显。

图2 蓄水100天后竖向位移等值线(m)

图3 蓄水300天后竖向位移等值线(m)
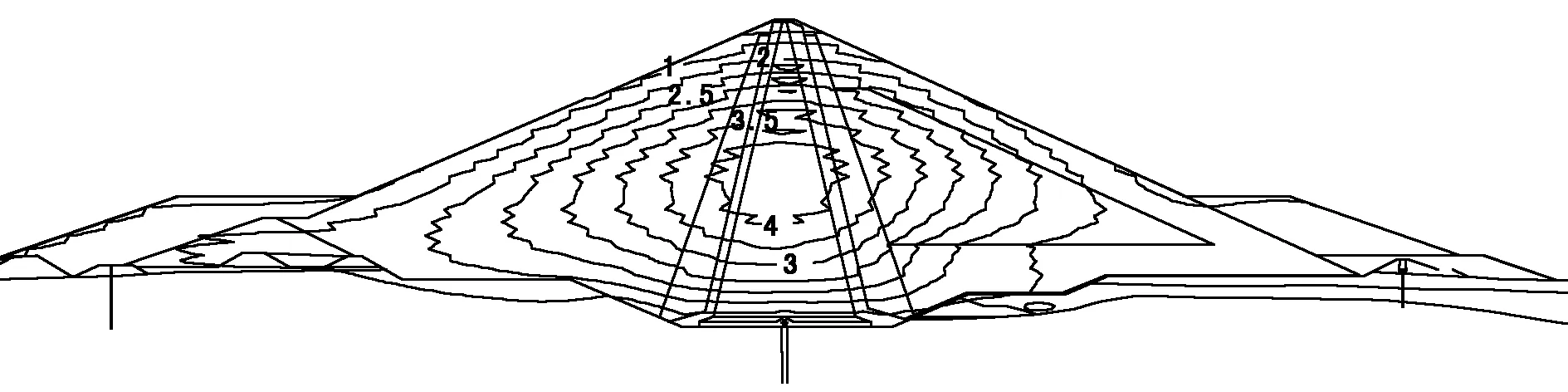
图4 蓄水500天后竖向位移等值线(m)
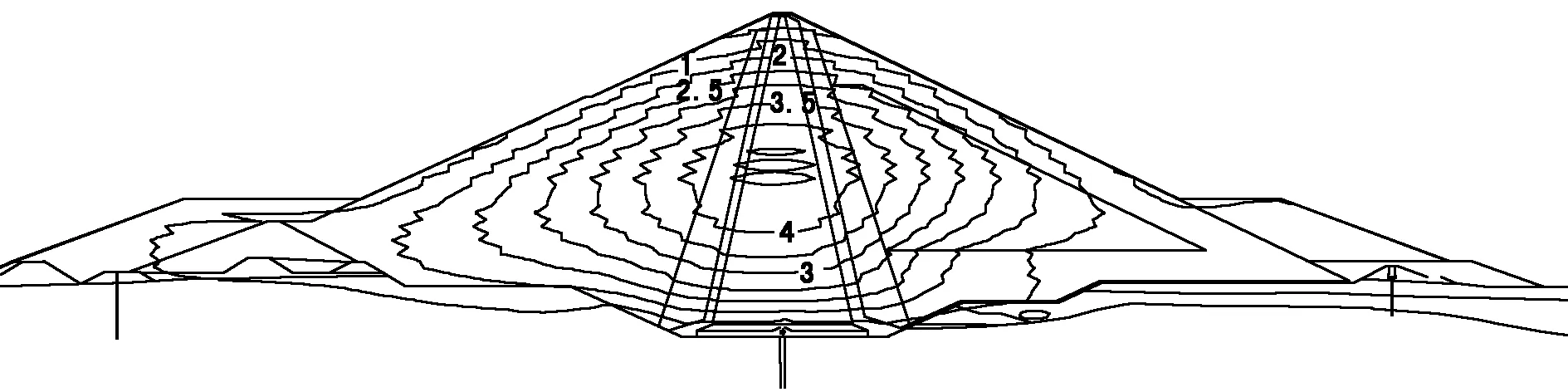
图5 蓄水600天后竖向位移等值线(m)

图6 蓄水100天后水平位移等值线(m)
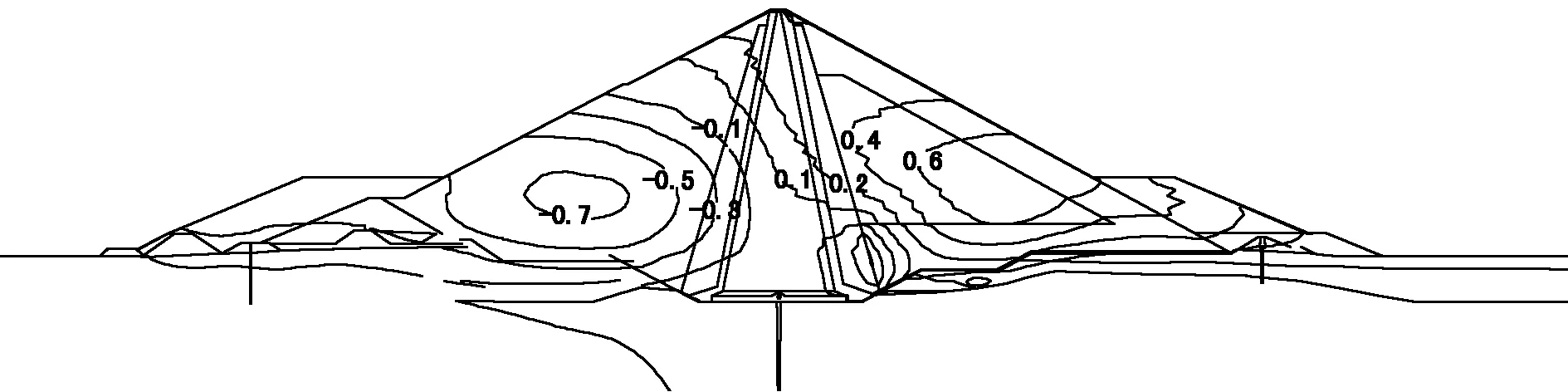
图7 蓄水300天后水平位移等值线(m)

图8 蓄水500天后水平位移等值线(m)

图9 蓄水600天后水平位移等值线(m)
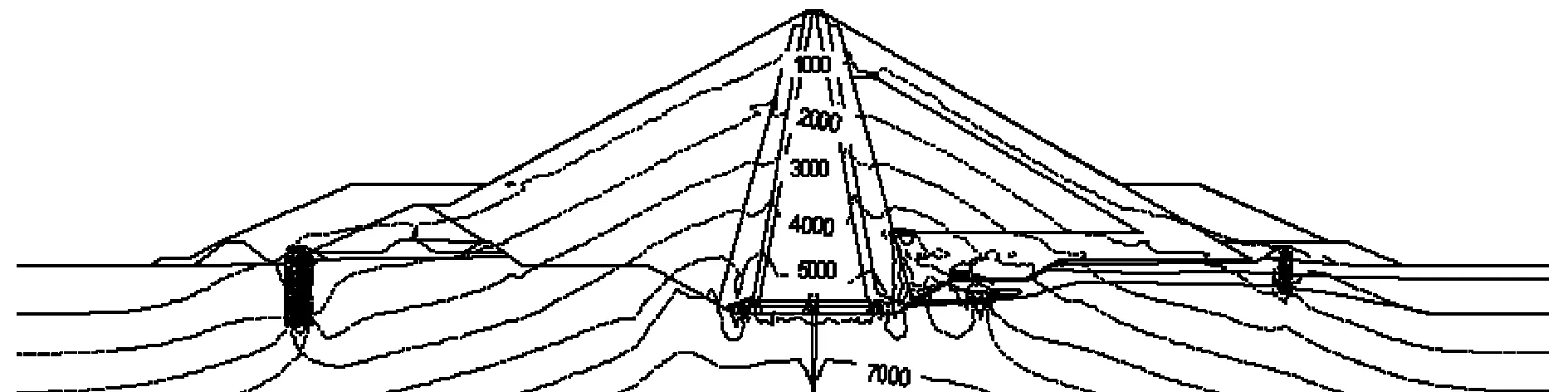
图10 蓄水100天后大主应力等值线(kPa)

图11 蓄水300天后大主应力等值线(kPa)

图12 蓄水500天后大主应力等值线(kPa)

图13 蓄水600天后大主应力等值线(kPa)
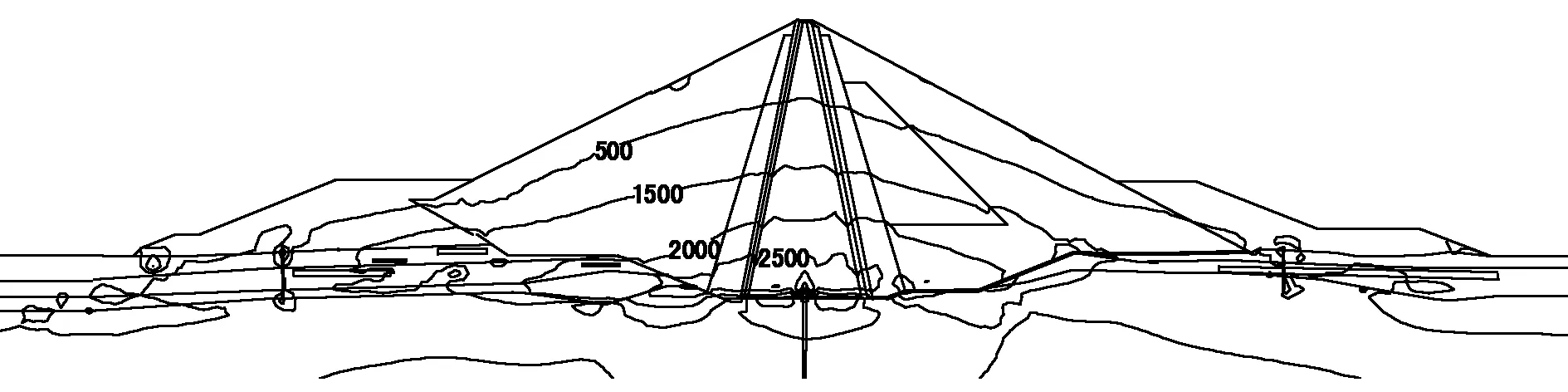
图14 蓄水100天后小主应力等值线(kPa)

图15 蓄水300天后小主应力等值线(kPa)
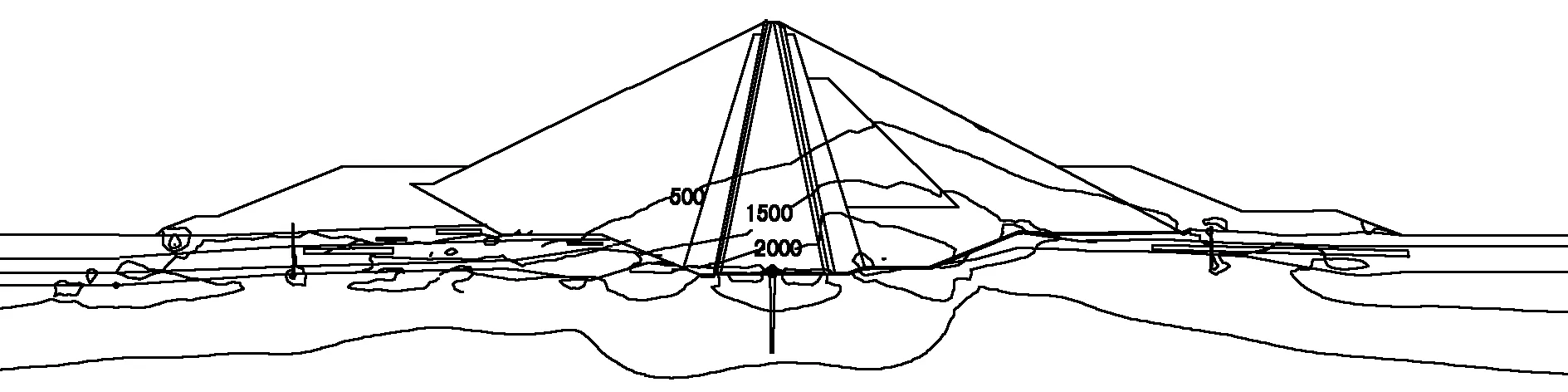
图16 蓄水500天后小主应力等值线(kPa)

图17 蓄水600天后小主应力等值线(kPa)
(2)对于坝体的应力,在蓄水过程中,大主应力变化较小,几乎维持不变,小主应力随着蓄水水位的增高,逐渐减小,有效应力在浸润线以下随着水位的增高也逐渐减小。
参考文献:
[1] 陈晓平,茜平一,梁志松,张芳枝,吴起星.非均质土坝稳定性的渗流场和应力场耦合分析[J].岩土力学,2004,25(6): 860-864.
[2] 钱家欢,殷宗,泽.土工原理与计算[M].第 2 版.北京:中国水利水电出版社,1996.
[3] 刘万忠,周志芳.基于GEO2SLOPE的土石坝应力场 ─ 渗流场耦合分析[J].勘察科学技术,2005(2):15-18.

