影子价格非唯一性的经济学解释
, ,
(1.石家庄铁道大学 经济管理学院,河北 石家庄 050043;2.石家庄铁路职业技术学院,河北 石家庄 050041)
一、引言
1939年,前苏联数理经济学家,线性规划理论的创始人之一康托洛维奇(L.V.Kantorovich)在《组织和计划生产的数学方法》一书中提出了所谓的“解乘数法”的方法,该方法以充分考虑资源的机会成本为核心思想进行生产的最优安排,其解就是现在所谓的影子价格。
影子价格是运筹学应用于经济学的一个重要概念,是运筹学成功处理经济问题的重要标志之一。正确认识和深刻理解资源影子价格的含义,对如何合理利用和节省资源,优化经济结构和提高经济效益都有着重要的参考价值和指导意义。按照运筹学的相关理论,不失一般性,若有生产问题的线性规划模型:
maxz=CX
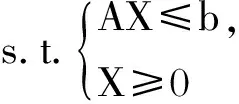
则其对偶问题的规划模型为:
minz=Yb
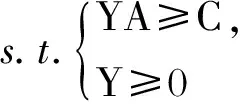
其中:X=[x1,x2,…,xn]T为决策变量,如产品的生产计划;C=[c1,c2,…,cn]为产品的价值系数;A为生产产品对资源的消耗系数;b=[b1,b2,…,bm]T为资源的拥有量。
这样定义后,对偶变量Yi即为原问题中第i种资源的影子价格,它是对第i种资源在生产中所做贡献的估价。从数值上看,Yi表示第i种资源每改变一个单位时,目标函数的改变量。在纯市场条件下,某种资源的市场价格低于影子价格时,可以买进这种资源;相反市场价格高于影子价格时,就应该卖出这种资源。特别地,当资源的影子价格为0时,表明该种资源未得到充分利用,处于资源闲置的状态;当该种资源的影子价格不为0时,表明该种资源在生产中已经消耗完毕,处于资源紧缺的状态。
尽管影子价格的定义早在19世纪40年代就已经被提出,但一直存在着诸多争议,其中最重要的争议之一是影子价格的非唯一性问题。国内已有不少文献对线性规划中影子价格的非唯一性进行研究,如马赞甫[1],夏少刚[2-3],刘舒燕[4]等都注意到了影子价格非唯一性问题,并得到了一些很有价值的结论。资源的稀缺性是在经济生活中面临的最重要的问题,而影子价格恰恰提供了一种衡量资源稀缺程度的方法,因此对影子价格的相关问题展开讨论是必要的和有益的。在对文献进行综述的基础上,从直观的图解法以及经济学的角度给出了影子价格非唯一性的合理解释。
二、问题的提出
从一个实际案例引入影子价格的非唯一性问题。假设有如下生产计划问题:某企业计划生产两种产品,这两种产品都要分别在A、B、C、D四个不同设备上加工。生产每件产品需占用的各种设备资源以及每种产品的单位利润如表1所示。
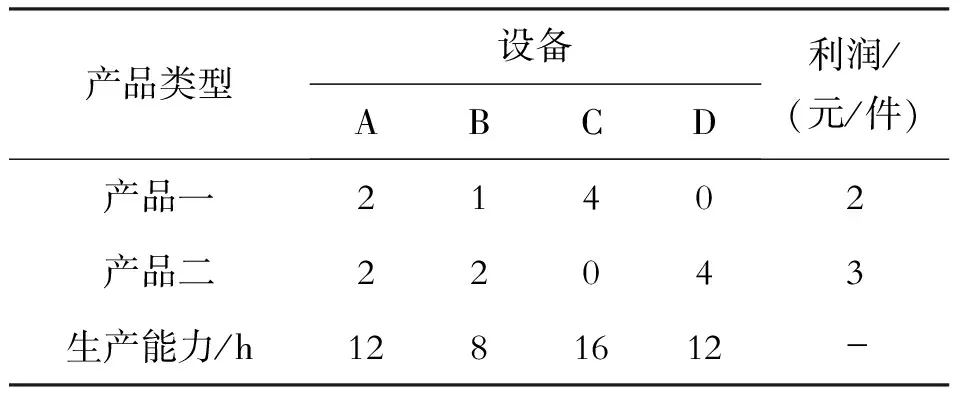
表1 生产基本情况表
这属于运筹学中一个简单的生产计划问题,为求解该问题可建立如下数学模型(为后面叙述方便,将原模型记为模型1,将其对偶问题的数学模型记为模型2):
模型1(原模型):
maxz=2x1+3x2
该问题的对偶数学模型2为:
minw=12y1+8y2+16y3+12y4
从通解中看出,对偶问题的解不是唯一的,随着k值的改变而改变。对偶问题解的不唯一性导致A、B、C、D四种资源的影子价格是不唯一的。当资源的影子价格不唯一时,就无法有效判断资源的稀缺程度,并且会对企业生产决策产生影响。例如:A资源的影子价格可以为0(当k=1/8时),也可以为1/2(当k=0时)。那么A资源对该企业是否紧缺呢,或者说其稀缺程度如何衡量呢?如果其影子价格为0,则根据上面的叙述,A资源对该企业就不是紧缺的,在一定范围内增加或减少A资源对该企业的利润不会产生影响;而如果其影子价格为1/2,A资源对该企业就是紧缺的,如果企业从市场上以价格p(p≤1/2)购买1单位A资源,则企业的利润可以增加1/2-p。由此可见,影子价格的唯一性对企业的决策是非常重要的。
针对对偶问题解的不唯一性,提出下面4个需要解决的问题:
(1)什么原因导致对偶问题的解是不唯一的;
(2)影子价格的非唯一性会对经济分析产生什么影响;
(3)如何从经济学角度解释解的非唯一性;
(4)解不唯一时影子价格应如何确定。
三、影子价格非唯一性的原因分析
为对影子价格非唯一性有一个直观的认识,首先采用图解法进行分析。利用运筹学相关方法,画出该生产计划安排问题数学模型的可行域,如图1所示。图中[1]、[2]、[3]、[4]每条线为模型1中依次四个限制条件所对应的直线方程,阴影部分为可行域,O点为最优点。从图1中可以看出,该模型最优解正好处于[1]、[2]、[3]三条直线的交点上。
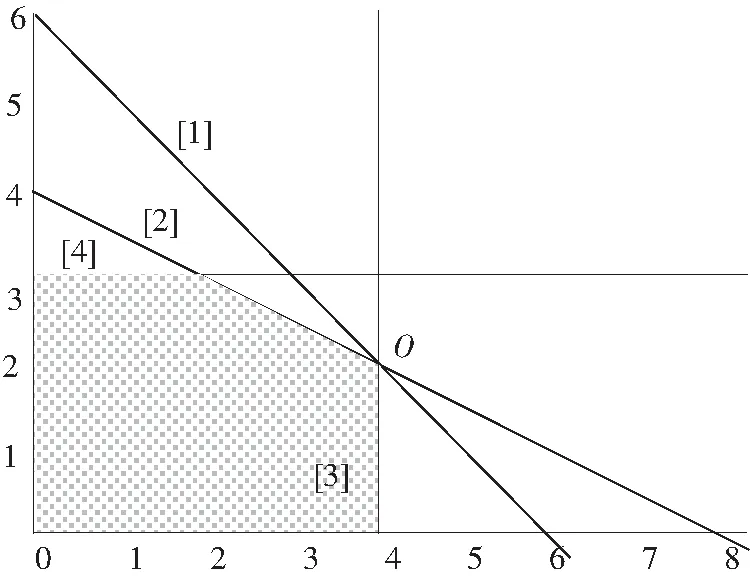
图1 原模型的可行域
现在将资源A增加一单位,即将第1个限制条件改为2x1+2x2≤13,改变后,模型的可行域如图2所示,图2中直线[1/]对应修改后的限制条件1。从图2中可以看出,虽然资源A增加一单位后,第1个限制条件对应的直线向右上方发生移动,但因第2、3个限制条件不变,因此模型的可行域并没有增加,模型的最优值也没有改变,仍然位于O点。
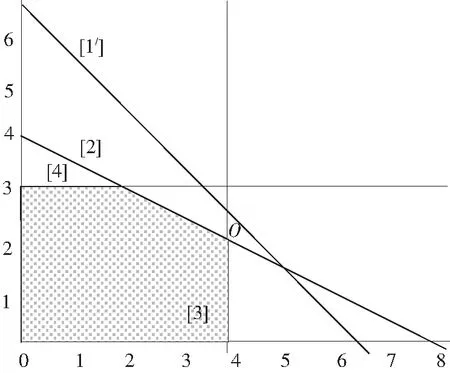
图2 资源A增加一单位后的可行域
如果在资源A增加一单位的基础上,再将资源B也增加一单位,即将第2个限制条件改为x1+2x2≤9,模型的可行域如图3所示,图3中直线[2/]对应修改后的限制条件2。从图3中可以看出,资源A和B同时增加时使得模型的可行域增加,最优值从O提高到O/点(此时最优值为15.5)。
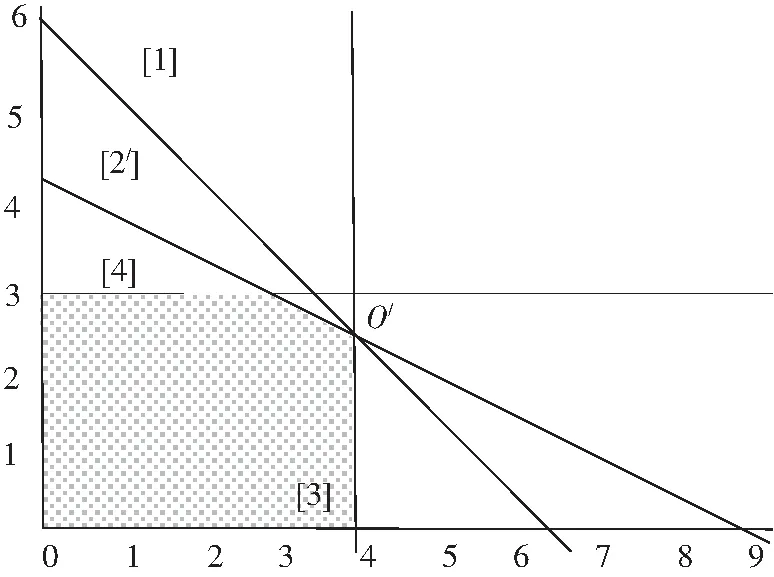
图3 资源A、B都增加一单位后的可行域
现在考虑另一种改变方式:在原模型基础上,将资源A减少一单位,即将第1个限制条件改为2x1+2x2≤11,改变后,按照上面的做法可以看出模型的可行域变小了,模型的最优值也相应的减小(此时最优值为13.5)。而如果在原模型的基础上仅将资源B增加一单位,即将第2个限制条件改为x1+2x2≤9,通过图解法可以看出,模型的可行域变大了,相应的最优值也得到增加(此时最优值为15)。另外,无论对资源D增加还是减少一单位,即无论第4个限制条件为4x2≤13还是4x2≤11,目标函数的最优值都不变。
上面这种最优点位于多个(两个以上)限制条件交汇处的情况在线性规划中称为退化。退化是指线性规划问题通过单纯形法求解时,最优解的某个基变量为0的现象。可以证明,若原问题的解是退化解,则其对偶问题的解不唯一,也即造成了影子价格的非唯一性问题。反之,若原问题的解不是退化解,则上述问题不复存在。
四、影子价格非唯一性的经济学解释
影子价格最重要的用途是进行决策和经济学解释,因此研究影子价格的经济学特征,利用经济理论分析影子价格的非唯一性问题是很有现实意义的。综合第三部分的图形分析,可以得出以下结论:
(1)当最优值处于多个(多于两个)限制条件对应直线的共同点时,这些限制条件对应资源的影子价格是不唯一的。
(2)当影子价格不唯一时,增加和减少某种资源的数量对最优值的影响是不同的。
(3)各种影子价格不唯一的资源拥有量改变时对目标函数的影响效果是不同的,即有些资源单独改变拥有量即可改变目标函数,有些资源必须和其他资源共同变化才能对目标函数产生影响。
(4)若某限制条件的对应直线不经过最优点,则该限制条件对应资源的影子价格为0。
利用生产要素需求的联合性和替代性,来解释影子价格非唯一性时产生的几种情况。按照经济学的理论,生产要素往往不单独发生作用。由于生产技术的特性,生产要素在生产时的需求具有共同性,或者联合性,即实际生产过程对多种生产要素的需求是共同的,相互依赖的。另外,生产要素之间又是可以相互替代的,其替代程度可以由生产要素的边际技术替代率(MRTS)来表示。边际技术替代率是指在技术水平不变的条件下,为维持同等的产量水平,放弃一定数量的某种投入要素而必须增加的另一种投入要素的数量。在经济学中可以通过等产量线来研究不同要素之间的可替代关系,以两种生产要素(分别记为L、K)为例,其等产量线如图4所示。
特殊的,当边际技术替代率为0时,两种生产要素必须按照一定的比例组合在一起才能够进行生产,产量是由按照比例最少的生产要素所决定的。例如农民锄地时,劳动力与锄头间的比例应该是1∶1,如果有100把锄头,而只有50个劳动力,则锄地的数量是由50个劳动力所决定的。图5给出了这种情况下的等产量线,其中的L,K表示两种不同的资源或生产要素。从图5可以看出,这种情况下的等产量线是折线,产量由折点对应的要素数量所决定。

图4 生产要素可替代时的等产量线
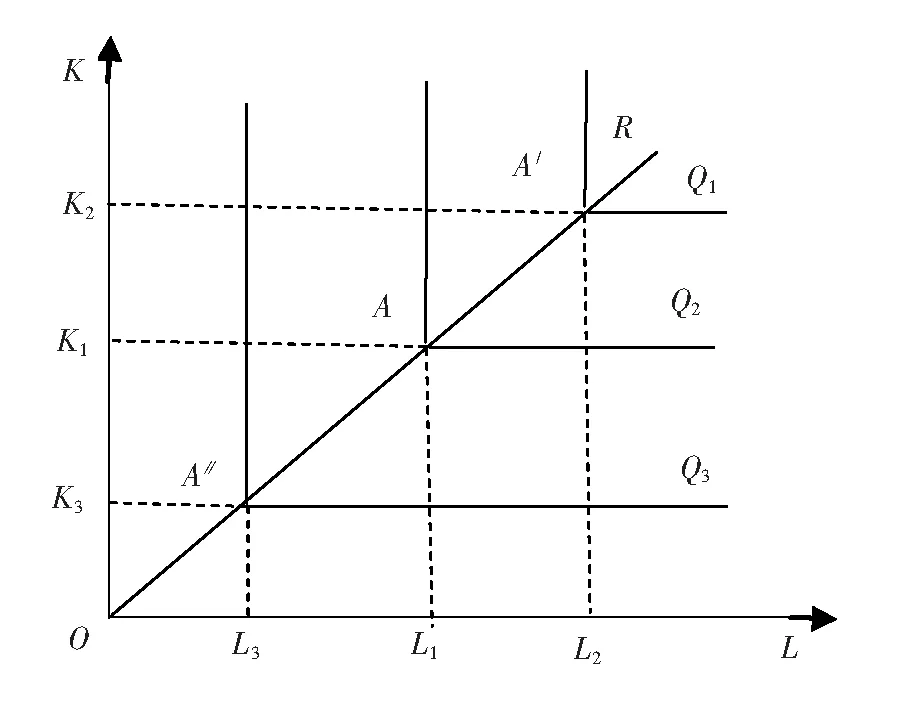
图5 生产要素固定比例的等产量线
在图4和图5中,当两种资源的数量为(L1,K1)时,产量为Q1。通过以下几种情况来分析要素的联合性及可替代性与影子价格的联系。
情况1:资源L的拥有量为L1保持不变,资源K由K1增加到K2。从图4可以看出,由于资源的可替代性,虽然资源L保持不变,但产量仍然从Q1增加到Q2;而从图5可以看出,由于两种资源的边际技术替代率为0,因此资源K的增加并没有引起产量的增加。这种情况可以解释为什么当影子价格不唯一时,资源拥有量改变对目标函数的影响效果是不同的。即当资源的边际技术替代率不为0时,单独改变该资源的拥有量即可改变目标函数,而当边际技术替代率为0时,单独改变该资源的拥有量不能改变目标函数。
情况2:资源L由L1增加到L2,同时资源K由K1增加到K2。从图4和图5可以看出,两种情况下产量都有所增加。这说明,当影子价格不唯一时,多种资源的共同变化能够对目标函数产生影响。
情况3:资源L的拥有量保持不变,资源K由K1减少到K3。从图5可以看出产量减少到Q3,结合情况1可以解释,为什么当影子价格不唯一时,增加和减少某种资源的数量对最优值的影响是不同的。
通过上面的分析,得出了影子价格非唯一性的原因,以及当影子价格不唯一时对经济分析产生哪些影响并给出了经济学解释,下面通过实例说明当影子价格不唯一时应如何确定资源的影子价格。
五、影子价格的确定
在经济学理论中,利润最大化问题的对偶问题是成本最小化,其对偶问题的最优成本可以看做企业取得最大化利润的机会成本。在完全竞争的经济环境中,企业的利润应该等于机会成本,这正好符合对偶问题的性质:原问题与对偶问题的最优值相等。因此,影子价格(对偶问题的解)的可以看做是在对偶问题的背景下研究如何使得资源利用的机会成本最小。
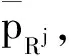
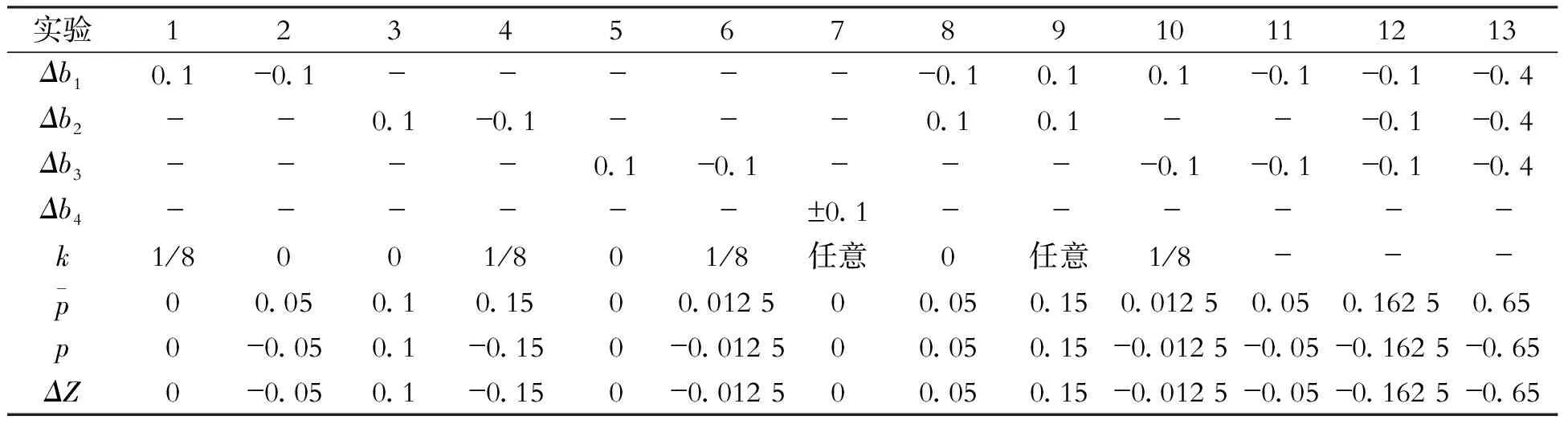
表2 资源改变量与目标函数值的对应关系
表2同时给出了利用软件LINGO11.0计算出的每次实验目标函数的改变量ΔZ,从计算结果可以看出,p=ΔZ。由此看出,虽然对于退化问题而言,具体资源的影子价格失去了意义,然而针对资源组合而言,影子价格是唯一给定的,可以用来进行经济分析。例如在实验13中,将资源1、2、3看做一种资源组合,在现有资源量的基础上,当该种资源组合中的每种资源都减少0.4时,其资源组合影子价格为0.65,若市场收购这种组合资源,则企业能够接受的价格应大于等于0.65,否则企业应保留该资源组合,用于自己生产。
六、结束语
通过具体实例,利用经济学相关理论,较为详细地分析了影子价格非唯一性的相关问题,并得到以下两个方面的结论:
(1)利用经济学中生产要素的联合性和替代性,可以合理解释影子价格的非唯一性。
(2)当影子价格非唯一时,在机会成本增加量最小的意义上,组合资源的影子价格是有效的。
参考文献:
[1]马赞甫. 线性规划中影子价格的“非唯一性”[J].系统工程, 2007, 25(4): 119-122.
[2]李敏, 夏少刚. 关于临界资源影子价格的再讨论[J].东北运筹与应用数学, 1998(10):109-114.
[3]夏少刚,张修来. 对“影子价格”定义的补充意见[J].运筹与决策, 1992,2(10):1914-1918.
[4]刘舒燕. 关于资源影子价格不唯一性问题的讨论[J].运筹与管理, 2001, 10(2):33-36.
[5]李敏. 资源的影子价格与对偶最优解的非唯一性[J].哈尔滨师范大学自然科学学报, 2004, 20 (2):27-29.

