基于偏微分方程去躁的磁共振电阻抗成像

李小霞， 王泽文， 何碧琴

(东华理工大学理学院数学系，江西南昌 330013)

基于偏微分方程去躁的磁共振电阻抗成像

李小霞， 王泽文*， 何碧琴

(东华理工大学理学院数学系，江西南昌 330013)

介绍了医学成像技术中磁共振电阻抗成像(MREIT)的数学模型和调和Bz算法。为克服调和Bz算法的不适定性，提出了一种偏微分方程去躁方法对Bz的躁声数据进行去噪。结合截断奇异值分解(TSVD)正则化方法，给出了基于Matlab偏微分方程工具箱的磁共振电阻抗成像的数值算法。用两个数值模拟算例验证了算法的有效性。

不适定问题;磁共振电阻抗成像;栯圆型方程反问题;偏微分方程;图像去噪

磁共振电阻抗成像(Magnetic Resonance Electrical Impedance Tomography，简称MREIT)是近20年来出现的一种新型医学成像技术，它是电阻抗断层成像(Electrical Impedance Tomography，简称EIT)技术和磁共振成像(Magnetic Resonance Imaging，简称MRI)的融合。目前，这一新型的成像技术无论是在算法和数学理论上，还是在实验上均处于研究发展阶段。

早期MREIT成像算法主要是基于电流密度的迭代算法，具有代表性的有电流密度替代算法(Kwon et al，2002a，Khang et al，2002)、等电位法(Kwon et al，2002b)和CCVSR算法(Eyuboglu et al，2003)等。这些方法均需要磁感应强度B=(Bx，By，Bz)在三个坐标方向的所有测量数据，为获得这些测量数据则需要在MRI扫描仪中旋转待成像的物体，这在实际医学临床上是不现实的。为此，Seo等(2003)提出了一种不需要对生物体进行三维旋转，只需要主磁场方向上的分量Bz的电阻抗重构算法。因为该方法在迭代中用到ΔBz，故称为调和Bz算法。随后，Oh等(2003)对该方法进行了改进，根据求得的▽σ利用位势方法来反演出电导率σ，由此调和Bz算法的抗噪性能得到了一定程度的提高。调和Bz算法的提出，因为它不需要对生物体进行三维旋转，从而为MREIT的实际临床应用提供了可能。因此，调和Bz算法引起了广泛的关注。由此，也发展出了许多基于Bz数据的算法和实验方案，其中典型的代表有梯度Bz算法(Park et al，2004)、局部调和Bz算法(Seo et al，2008;Jeon et al，2010)等。

本研究首先给出了磁共振电阻抗成像的数学模型，利用位势理论的方法来重建电阻率。其次，提出了一种新的偏微分方程去噪方法对Bz数据进行去噪，结合截断奇异值正则化方法给出了磁共振电阻抗成像的算法，从而改善了算法的不适定性，提高了电阻率成像的分辨率。这是本研究的主要创新点。最后，给出了基于Matlab偏微分方程工具箱的数值模拟方案，同时给出了两个数值模拟例子来验证所给算法的有效性。

1 磁共振电阻抗成像的数学模型

众所周知，生物体内的电流分布决定于生物体内部的电导率，在后面的叙述中，称生物体为目标体，通过表面电极给目标体输入电流，从而产生电流J=(Jx，Jy，Jz)和磁感应强度B=(Bx，By，Bz)。根据它们之间的物理关系，可建立磁共振电阻抗成像的数学模型(Wang et al，2009，陈群等，2009，Liu et al，2007)，从而重建目标体内部的电导率分布。

设Ω表示待成像目标体在三维空间R3中的有界开区域，且其边界∂Ω是光滑的。记Ωz0:=Ω∩{z=z0}，且设Ωz0具有光滑的边界。假设Ω内的电导率σ(r)，r=(x，y，z)是各向同性的。在目标体的表面边界∂Ω上安置正负电极ε+和ε－，输入电流I，则在 Ω 内部产生了电流密度J=(Jx，Jy，Jz)，且满足

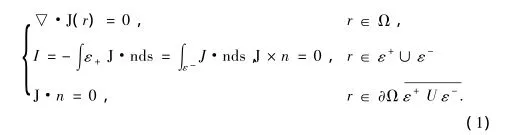
其中n是∂Ω上的外法线方向，▽是梯度算子。因为目标体内部的电流J(r)、电位u(r)、电导率σ(r)三者之间满足安培定律J(r)=－σ(r)▽u(r)，所以(1)式可以表示成椭圆型方程的边值问题。

众所周知，磁共振电阻抗成像的调和Bz算法是不适定的。不适定问题是应用数学与计算数学的一个重要研究内容(张小明等，2009;葛美宝等，2006)。调和Bz算法的不适定性主要表现在以下两方面:一是在求解方程(7)之前，需计算右端项ΔBz，即需要由Bz的噪声数据计算其二阶偏导数，这是个严重的不适定问题;二是方程(7)中系数矩阵A也是近似奇异的(Seo et al，2008)，即该方程是个不适定的线性方程组。对于第一个不适定性，将提出一种偏微分方程去噪模型来处理带有噪声的Bz数据，从而克服计算ΔBz的不适定性;对于第二个不适定性，采用截断奇异值正则化方法来求解方程(7)。由于截断奇异值正则化方法是个成熟的算法且很容易在相关文献中找到，故不再列出。

2 基于偏微分方程的去躁方法

Lee et al.(2005)提出了一种高斯曲率驱动的偏微分方程的图像去噪模型。但是，在数值模拟时发现该去噪模型的收敛速度比较慢。为此，结合文Song(2003)中提出了一种基于L1+ε(0＜ε＜1)范数的自适应TV去噪模型ut=▽·(|▽u|p－2▽u)－λ(u－u0)，1＜p＜2，提出一种新的偏微分方程去噪模型:

3 基于Matlab的数值模拟方案

Matlab软件的偏微分方程工具箱(PDE Toolbox)提供了一个研究和求解二维偏微分方程问题的强大而又灵活的环境。PDE Toolbox求解的基本方程有椭圆型方程，抛物线方程，双曲线特征方程，椭圆型方程组以及非线性椭圆方程。为了进行数值模拟，本文利用偏微分工具箱求解磁共振电阻抗成像正问题，从而获得测量数据。为此，需进一步在二维空间对共振电阻抗成像的数学模型进行分析研究。二维空间中的磁共振电阻抗成像模型是三维空间中的无限长柱体模型的简化，即Ω:=D×R1，其中D∈R2，进一步假设Ω中的电导率和注入的电流I与z轴均无关。

4 数值模拟

在二维空间的有界域D=［－1，1］×［－1，1］上，取q=2，利用算法2进行数值模拟，也就是在三维空间中Ω的一个切片上进行数值模拟。为了验证此算法的稳定性，给Bz数据加上噪声数据

例1 真实电导率图像为“6”和“8”两个数字，见图1a。计算结果见图2～3。

算例1中，给出了数字“68”的真实电导率图像(图1a)和无噪声下电导率的重建图像(图1b)，当加入噪声水平为δ=0.005时，电导率的重建图像为图2。当加入噪声水平为δ=0.01时，电导率的重建图像为图3。重建电导率图像的效果表明:提出的基于偏微分方程去噪的重建算法消除了高频噪声的影响，很好的保持了图像的边缘，得到了更好的电导率重建效果图。

例2 医学图像“OK”手形的电导率重建，给定一幅人的“OK”手形的X光射线图像，如图4a，计算结果见图5和图6。

在算例2中，给出了“OK”手形的真实电导率图像(图4a)和无噪声下电导率的重建图像(图4b)。当加入噪声水平为δ=0.005时，电导率的重建图像为图5。当加入噪声水平为δ=0.01时，电导率的重建图像为图6。同样，可以看出经偏微分方程去噪后，重建的电导率图像分辨率更高，且很好地保持了图像的边缘。

陈群，黄标昌，刘继军.2009.介质电导率成像数值反演的正则化方法［J］.计算数学，31(1):51-64.

葛美宝，徐定华，王泽文，等.2006.一类抛物型方程反问题的数值解法［J］.东华理工学院学报，29(3):283-288.

张小明，王泽文，王燕.2009.一类热传导方程多点源反演的唯一性和稳定性［J］.东华理工大学学报，32(2):189-193.

Eyubolu O，Ider Y Z.2003.Current constrained voltage scaled reconstruction(ccvsr)algorithm for mr-eit and its performance with different probing current patterns［J］.Phys Med Biol，48:653-671.

Jeon K，Kim H J，Lee C O.2010.Integration of the denoising，inpainting and local harmonic Bzalgorithm for MREIT imaging of intact animals［J］.Physics in Medicine and Biology，55:7541-7556.

Khang H S，Lee B I，Oh S H，et al.2002.J-substitution algorithm in magnetic resonance electrical impedance tomography(MREIT):phantom experiments for static resistivity images［J］.IEEE Trans Med，21:695-702.

Kwon O，Lee J Y，Yoon J R.2002b.Equipotential line method for magnetic resonance electrical impedance tomography［J］.Inverse Problems，18:1-12.

Kwon O，Woo E J，Yoon J R，et al.2002a.Magnetic resonance electrical impedance tomography(mreit):simulation study of j-substitution algorithm［J］.IEEE Trans Biomed Eng，49:160-167.

Lee S H，Seo J K.2005.Noise removal with Gauss curvature-driven diffusion［J］.IEEE Transactions on Image Processing，14(7):904-909.Liu J J，Seo J K，Sini M，et al.2007.On the convergence of the harmonic Bzalgorithm in magnetic resonance electrical impedance tomography［J］.SIAM J Appl Math，67(5):1259-1282.

Oh S H，Lee B I，Woo E J，et al.2003.Condutivity and current density image reconstrucion using harmonic Bzalgorithm in magnetic resonance electrical impedance tomography［J］.Phys Med Biol，48(19):3101-3116.

Park C，Kwon O，Woo E J，et al.2004.Electrical conductivity imaging using gradient Bzdecompositon algorithm in magnetic resonance electrical impedance tomography(MREIT)［J］.IEEE Trans Med Imaging，23(3):388-394.

Seo J K，Kim S W，Kim S，et al.2008.Local harmonic Bzalgorithm with domain decomposition in MREIT:computer simulation study［J］.IEEE Trans Med Imaging，27(12):1754-1761.

Seo J K，Yoon J R，Woo E J，et al.2003.Reconstruction of conductivity and current density imaging using only one component of magnetic field measurements［J］.IEEE Trans Biomed Eng，50(90):1121-1124.

Song B.2003.Topics in Variational PDE Image Segmentation，Inpainting and Denoising［Ph.D］.USA:University of California Los Angel-es.

Wang Z W，Qiu S F.2009.Electrical Conductivity Imaging Using A Hybrid Regularization Method in Magnetic Resonance Electrical Impedance Tomography［C］.Proceedings of the 2nd International Conference on Biomedical Engineering and Informatics，1-5.

Magnetic Resonance Electrical Impedance Tomography Based on PDE-based Noise Removal

LI Xiao-xia， WANG Ze-wen， HE Bi-qin
(Department of Mathematics，School of Science，East China Institute of Technology，Nanchang，JX 330013，China)

In this study，the reconstruction algorithm of magnetic resonance electrical impedance tomography is studied.First，we introduce the mathematical model of magnetic resonance electrical impedance tomography and the harmonic BZalgorithm.In order to overcome the ill-posedness of the harmonic BZalgorithm，a PDE-based denoising technique is proposed to process the noise data of BZ.Then，combining with the truncate singular value decomposition regularization method，an algorithm of magnetic resonance electrical impedance tomography based on the Matlab PDE-tool is developed.Finally，two numerical examples are presented to verify the efficiency of the algorithm.

ill-posed problem，magnetic resonance electrical impedance tomography，inverse problems for elliptic equations，partial differential equation，image denoising

O24

A

1674-3504(2012)01-094-07

李小霞，王泽文，何碧琴.2012.基于偏微分方程去躁的磁共振电阻抗成像［J］.东华理工大学学报:自然科学版，35(1):94-100.

Li Xiao-xia，Wang Ze-wen，He Bi-qin.2012.Magnetic Resonance Electrical Impedance Tomography Based on PDE-based Noise Removal［J］.Journal of East China Institute of Technology(Natural Science Edition)，35(1):94-100.

10.3969/j.issn.1674-3504.2012.01.014

2011-08-29 责任编辑:张国庆

国家自然科学基金(10861001);江西省自然科学基金(2009GZS0001，2010GZS0010)

李小霞(1987—)，女，硕士生，研究方向:数学物理反问题。

*通讯作者:王泽文.E-mail:zwwang@ecit.cn