需求信息共享供应链系统稳定域内的优化
王 晶 杨 欢 韩伟伟
(北京航空航天大学 经济管理学院,北京100191)
供应链管理水平对企业的竞争能力有重要影响,因此,供应链系统的优化设计是企业供应链管理的核心内容之一.通过供应链系统的优化设计,可以改善企业的物流活动,降低企业的生产经营成本,进而提高企业的整体供应链绩效水平.供应链的稳定运行是保证供应链整体优化和长期竞争优势的必要条件.从这个意义上看,供应链的稳定性[1-2]是供应链的重要绩效指标.国内外关于供应链及其优化的研究成果很多[3],涉及的供应链种类繁多,优化方法各异,但绝大部分采用遗传算法.供应链优化建模标准也有不同,以供应链价值最大化、交货费用最小化和供应链成本最小化等作为优化目标的研究较为普遍.文献[4]用控制论的方法研究供应链系统优化问题,对库存控制系统通过遗传算法进行了优化,定义了5个优化指标:库存恢复能力、噪声带宽、生产稳定性、在制品信息滞后稳定性和选择性,取这些指标的加权平均值作为优化目标.文献[5]研究了供应商管理库存(VMI,Vendor Managed Inventory)供应链系统动态响应特性的优化,优化目标为分销商与系统的库存恢复能力和噪声带宽的加权平均值.
本文针对需求信息共享的二级供应链系统,研究在其稳定域内进行系统优化的问题.首先通过考察系统参数对系统稳定性的影响,确定系统的稳定域;然后利用多目标算法NSGA-Ⅱ考察系统稳定性指标在系统稳定域内的最优解的分布情况;最后分析系统参数对系统最优状态下的各种稳定性指标的影响,研究最优参数的不同取值对提高系统整体稳定性的决策意义.
1 需求信息共享的供应链系统模型
文献[6]利用系统动力学方法提出了APIOBPCS(Automatic Pipeline Inventory and Order Based Production Control System)模型,在此基础上,文献[7-8]建立了需求信息共享(DIS,Demand Information Sharing)二级供应链系统模型(DIS-APIOBPCS),模型中包含制造商和分销商.该系统模型的框图如图1所示.
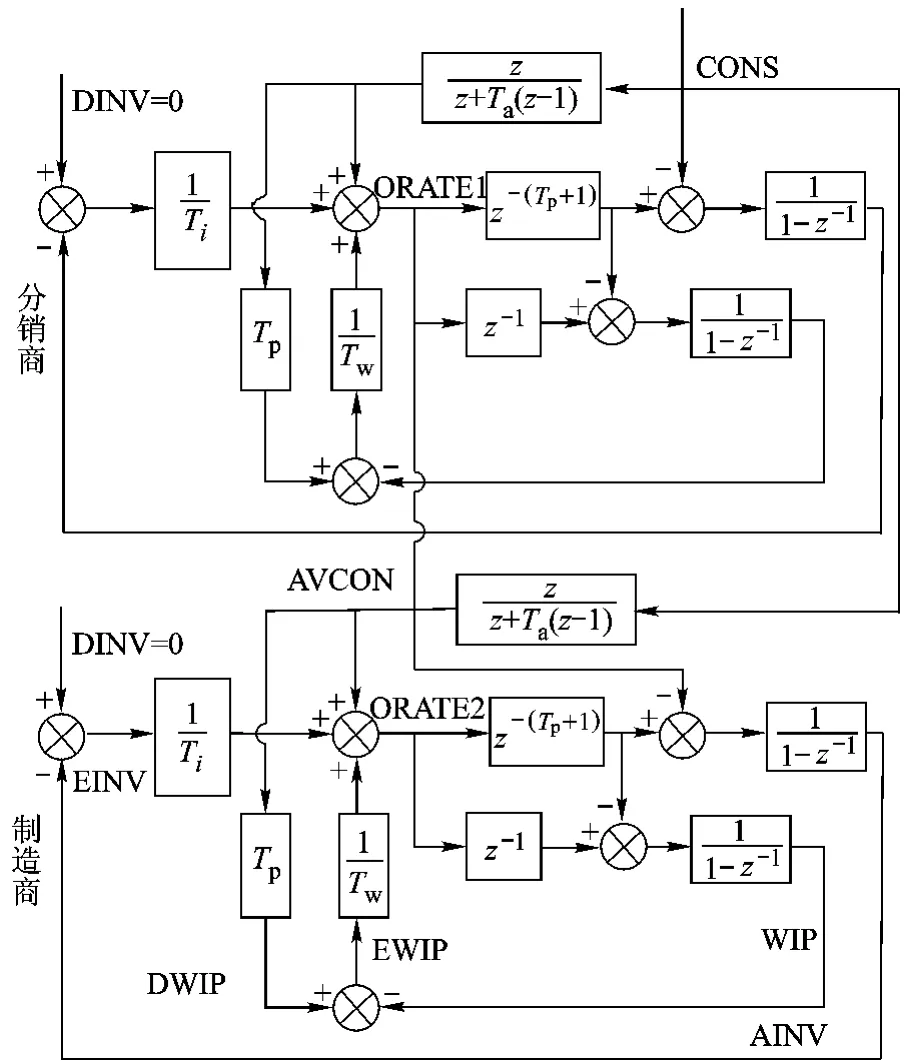
图1 需求信息共享二级供应链系统模型
本文针对这种需求信息共享二级供应链系统,研究在其稳定域内进行系统稳定性指标的优化问题,使用的供应链系统变量如下.

需求预测:
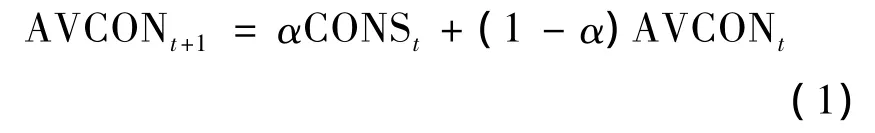
期初库存:
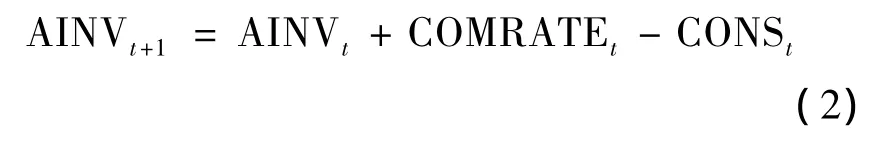
期初在制品:
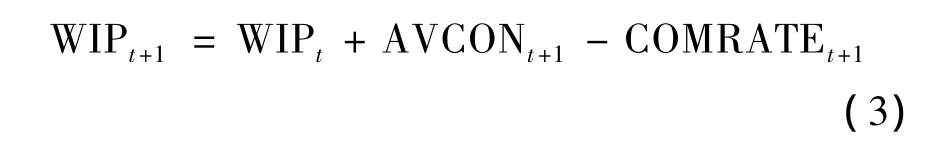
到货量:
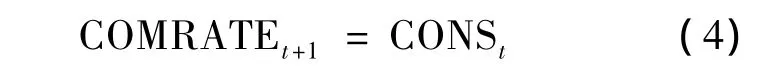
据文献[9]可知 DIS-APIOBPCS系统中,制造商的订货量的传递函数为
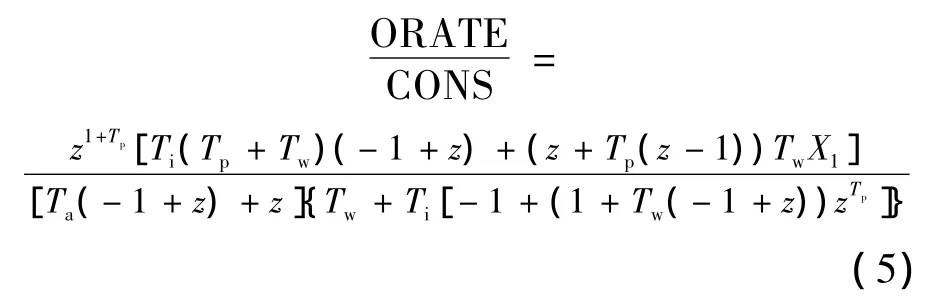
其中
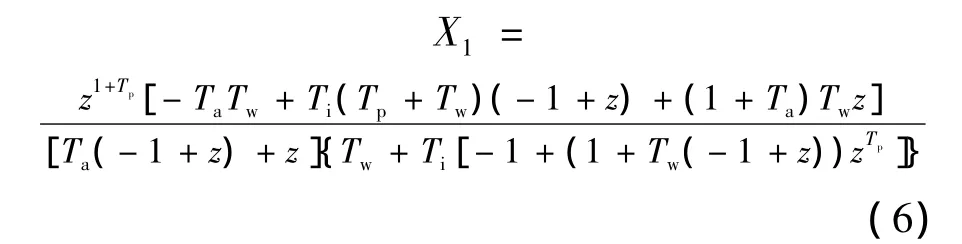
式中,Ta为需求预测数据的平滑期数,Ta=(1-α)/α,其中α为使用指数平滑法进行需求预测时的平滑系数,Ta越小,需求预测在影响生产率的因素中权重越大;Tp为提前期参数;Ti为库存调节参数,描述库存偏差对生产率调节,Ti越小库存信息在影响生产率的因素中权重越大;Tw为在制品调节参数,描述在制品偏差对生产率调节,Tw越小,在制品信息在影响生产率的因素中权重越大.
假设在二级供应链中,制造商使用固定的平滑系数进行需求预测,而且系统的生产提前期也是固定的,则在保持Ta和Tp不变的情况下(Ta=5,Tp=1),通过仿真实验[9],可以确定该系统的稳定性区域如图2所示.在稳定域内中任意取4个特定的点A,B,C,D,针对这4种系统参数组合,对系统输入单位阶跃需求信号,分别得到系统订货量的响应曲线如图3所示.由图3可知,虽然A,B,C,D 4点代表的参数组合都在系统的稳定域内,但系统参数的不同组合所对应的系统的稳定性明显不同.若取A点的参数值,系统虽然最终会恢复稳定状态,但要经过一个剧烈的振荡过程;而若取D点的参数值,则对于需求变动,系统会平稳快速地达到稳定状态.以往有关供应链系统稳定性的研究主要关注确定系统的稳定域,而对于系统在稳定域内表现的需求响应特性却没有深入讨论.本文的目的是在明确了系统的稳定域之后,分析稳定域内各种参数组合对系统需求响应的影响,以实现对系统参数的优化,达到提高系统的稳定性和系统运行绩效的目的.
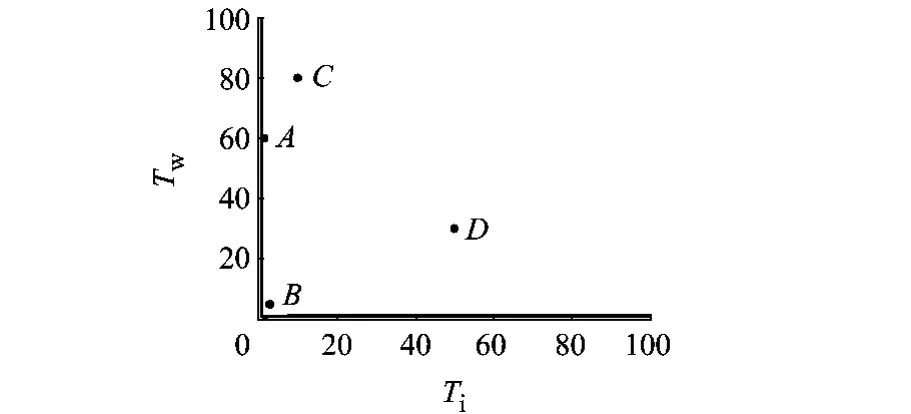
图2 二级供应链系统稳定域
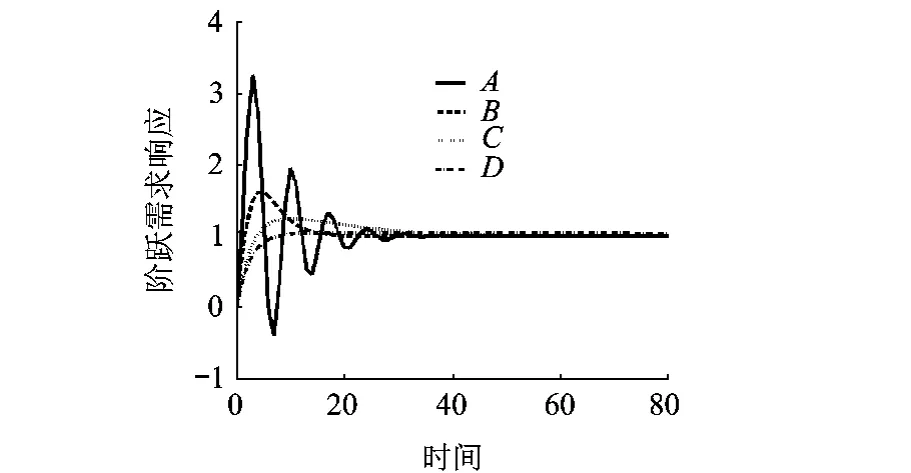
图3 A,B,C,D点的阶跃需求响应曲线
2 DIS供应链系统的最优化分析
本文对DIS-APIOBPCS模型阶跃需求响应特性进行系统优化分析,综合考察系统的库存响应、订单响应和牛鞭效应这3个系统响应特性,将其作为系统优化的目标.参考文献[4]就APIOBPCS库存优化的研究和文献[5]对供应商管理库存系统动态特性能的优化研究,根据对供应链系统稳定运行的要求,本文采用以下3种稳定性特性值作为系统优化指标.
ITAE(Integral of Time Absolute Error):库存阶跃响应误差的绝对值时间积分,是估计阶跃响应中实际库存量相对于目标库存量偏差的最直接的度量指标,用于衡量系统库存量恢复到稳态值的能力.
订单最大超调量(ORATE maximum deviation):订单响应曲线中最大超出量与稳态值之比,反映了系统响应过渡阶段的平稳性.
Wn:噪声带宽,是对供应链系统牛鞭效应的定量描述,是衡量Ta,Tw,Ti对需求信息平滑效果的指标,在确定订货量时,能过滤高频率的随机需求信息.本文采用Astrom在《随机控制理论导论》中提出的方法计算Wn,通过供应链系统订货量的传递函数中分子与分母关于z的系数向量计算Wn.
供应链中不同的系统参数组合会对上述3种稳定性指标产生不同的影响,本文使用多目标优化算法NSGA-Ⅱ考察供应链系统的优化指标,确定系统的最优参数组合,达到使系统在各个稳定性指标上均处于最优化状态的目的.多目标优化方法能克服通过加权将多个优化目标转化为单一优化目标的弊端,这些算法采用Pareto最优等概念把各子目标之间的折中和此消彼长的过程自然地融合到算法流程中,不必人为先验地确定各子目标之间的权重关系,可以同时兼顾多个目标的优化,提高分析和求解问题的能力.
多目标优化算法NSGA-Ⅱ是带精英策略的非支配排序遗传算法,是Deb等人在NSGA的基础上加入快速非支配排序算法、引入精英策略、采用拥挤度和拥挤度比较算子,使Pareto最优解前沿中的个体能均匀地扩展到整个Pareto域,保证了种群的多样性[5].NSGA-II算法的基本思想为:首先,随机产生一定规模的初始种群,非支配排序后通过遗传算法的选择、交叉、变异3个基本操作得到第1代子代种群;然后,从第2代开始,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群;最后,通过遗传算法的基本操作产生新的子代种群;依此类推,直到满足优化程序结束的条件.本文应用NSGA-Ⅱ算法对供应链系统稳定性的3个指标ITAE、订单最大超调量、Wn进行优化,设置优化搜索中种群代数为400代,种群规模为200个,最终确定使系统在这3个稳定性指标下处于Pareto最优的系统参数组合.
在4个主要系统参数中,需求预测参数Ta对供应链系统的稳定域没有影响,系统稳定性只由Tp,Ti,Tw决定[9].所以如果设定提前期参数 Tp,则系统的稳定域就被固定了.本文将考察在不同提前期参数设定下系统稳定性指标的优化问题.
2.1 Tp=1时系统稳定性指标的最优化
在提前期参数Tp=1时,系统的稳定性条件[9]为
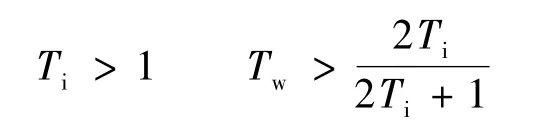
设定Tp=1,Ta=5,通过仿真分析得到的在稳定域内供应链系统的3个稳定性指标达到Pareto最优的分布图,如图4所示,可以看到这些点在空间中的分布具有较强的规律性.
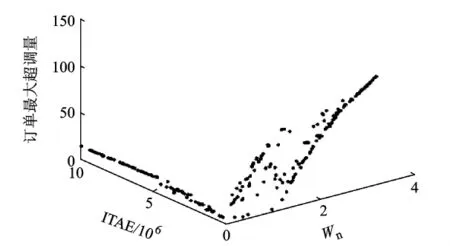
图4 Tp=1时系统稳定性指标订单最大超调量、ITAE、Wn最优时三维分布图
图5显示了供应链系统的3个稳定性指标处于Pareto最优时的系统参数取值情况,即Pareto最优解在稳定区域内的分布.
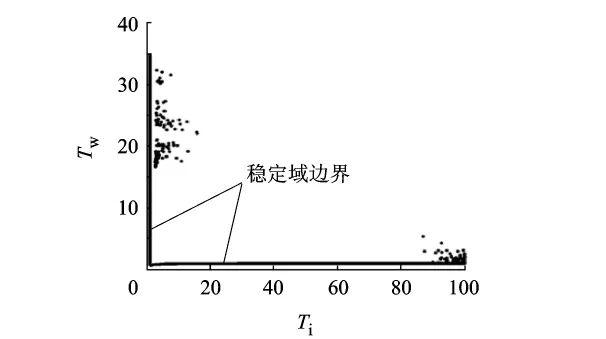
图5 Tp=1时DIS-APIOBPCS系统稳定区域内最优点
从图5也可以看出供应链系统稳定性指标的Pareto最优解在稳定域内的分布具有较强的规律性,使系统达到Pareto最优的系统参数并非均匀的分布在稳定域内,而是被限制在一定的取值范围内.其中Ti的取值范围集中分布在0~10及90~100之间;Tw的取值范围集中分布在0~5及15~30之间.
由于多目标优化问题的Pareto最优解是一个集合,如图5所示,所以稳定域内的最优点均可保证系统的3个稳定性指标处于Pareto最优状态.Pareto最优解集合中的每个点代表不同的稳定性指标组合,企业可以根据自己的实际情况选择合适的稳定性指标值.下面将进一步考察供应链系统在Pareto最优状态下,即系统参数在Pareto最优解范围内的变动对3个稳定性指标的影响.
图6所示为需求预测参数Ta对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.可以看出,Ta的取值与ITAE成正相关关系,当Ta取100时ITAE达到其最大值;而Wn和订单超调量却随着参数Ta取值变大,由最大值迅速下降并被限定在一个有限值的范围内.因此供应链系统稳定性指标可以分为2组,Wn和订单超调量及ITAE.这2组指标对于Ta表现出完全相反的行为模式.此时企业需要权衡Wn、订单超调量与ITAE之间的利弊关系,若企业希望避开ITAE的不利影响,需要取较小的Ta值以提高供应链运行的稳定性.反之,如果企业希望避免Wn与订单超调量过大,则需要取比较大的 Ta值.当 Ta值在10~90范围内时,3个指标值都处于较小的范围,如果企业认为较小的取值即可满足需求,可以在10~90范围内选择需求预测参数Ta.
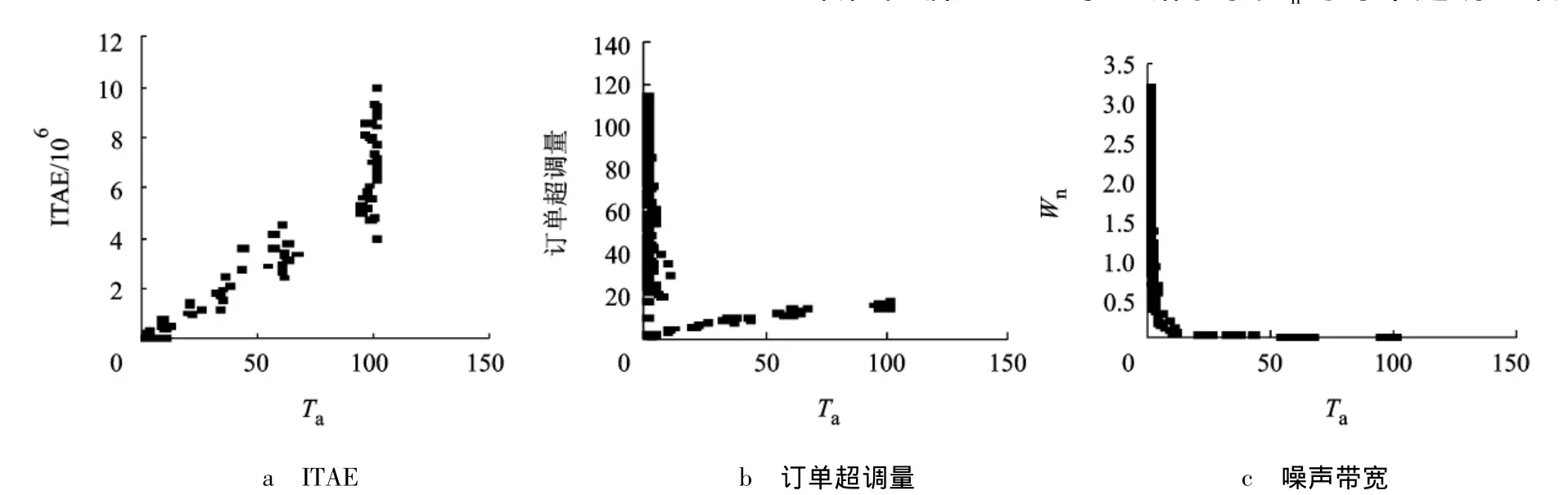
图6 Tp=1时Ta对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
图7为库存调节参数Ti对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.与图6的情况类似,Ti取值与ITAE成正相关关系,而与Wn和订单超调量成负相关关系.当Ti取值在临近100的区域内时,Wn与订单超调量取得最小值而ITAE却达到最大值.但是与图6不同的是,根据图5可知,Ti的取值在Pareto最优状态下有规律的分布在0~10及90~100之间,不像Ta可以在1~100内连续取值使3个性能指标都达到较小的值.所以通过Ti调节系统的稳定性时,在Pareto最优状态的范围内需要进行权衡,如果企业希望得到最小的Wn与订单超调量的值,就不得不以更大的ITAE值为代价.另一方面,如果企业希望得到更小的ITAE值,就不得不在Wn与订单超调量上做出妥协.因此,企业应认真地分析各稳定性指标的重要性,在此基础上选择合适的Ti的取值,以使供应链系统的稳定性指标达到企业的要求.
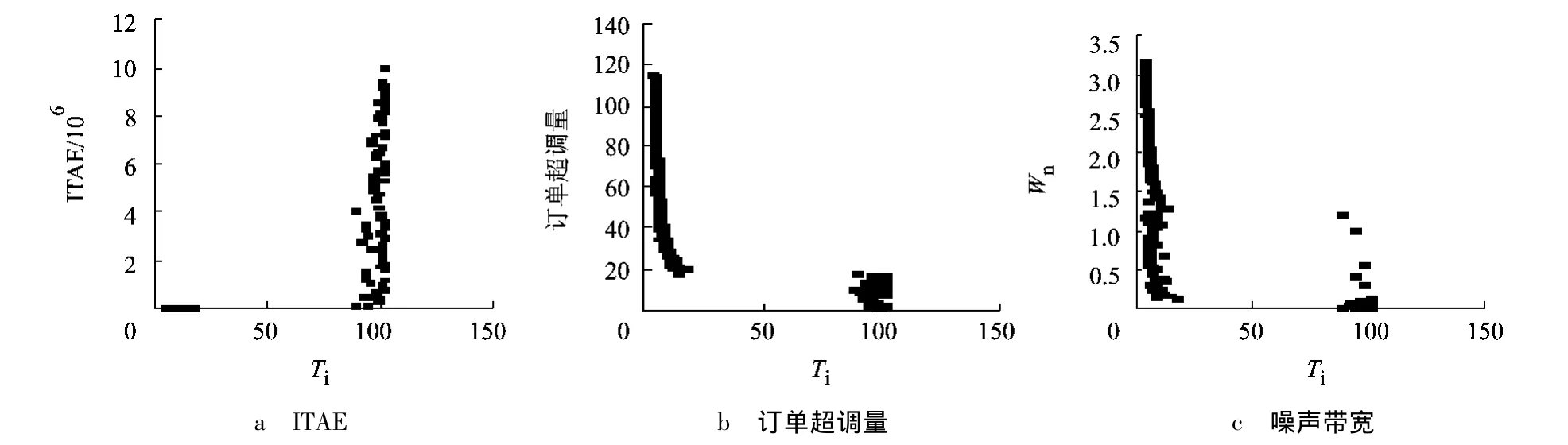
图7 Tp=1时Ti对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
图8为在制品调节参数Tw对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.
可以直观地发现,与图6和图7不同,Tw取值与ITAE成负相关关系,而与Wn和订单超调量成正相关关系.但是与图7相似的是,Tw的取值也有极强的规律性,为了达到Pareto最优状态,Tw的取值被限定在0~5及15~30之间.因此,ITAE同样又是和Wn与订单超调量表现出相反的行为模式.若企业希望避开ITAE的不利影响,可在一个很大的范围内选取较大的Tw值使ITAE最小.如果使Tw的取值很小,就能得到最小的Wn与订单超调量的值,从而提高供应链的稳定性.
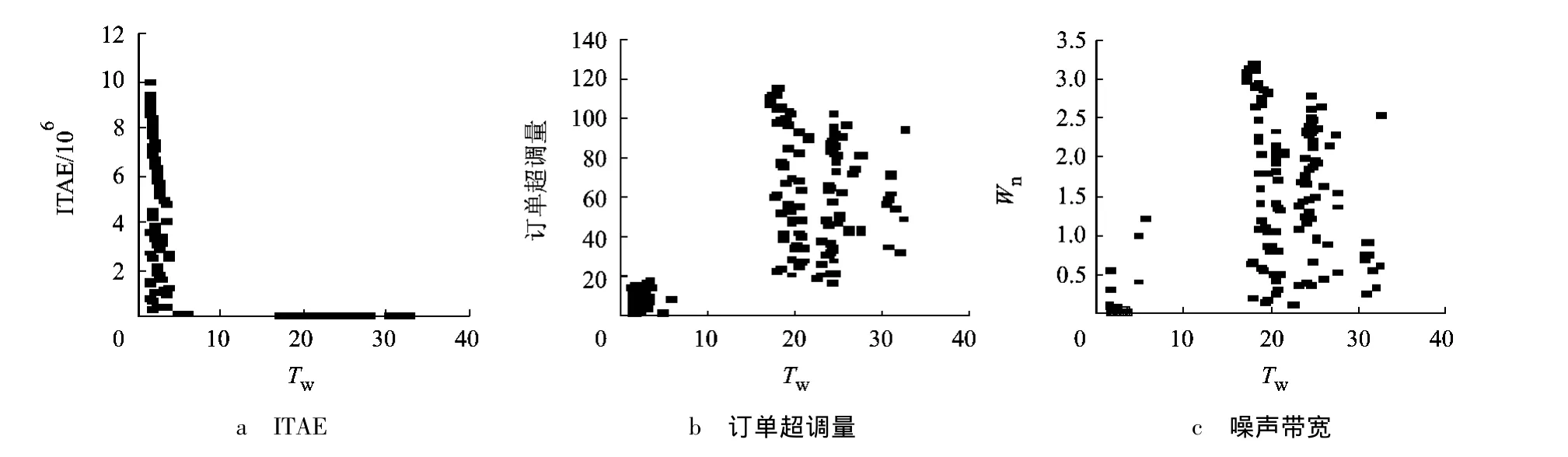
图8 Tp=1时Tw对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
2.2 Tp=2时系统稳定性指标的最优化
提前期参数Tp=2时,系统的稳定性条件[9]为
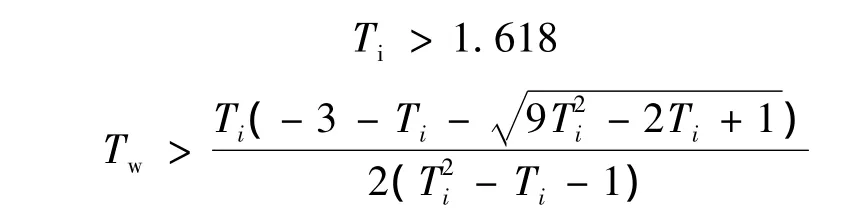
在设定提前期Tp=2情况下进行仿真实验,图9、图10分别显示了稳定域内供应链系统的3个稳定性指标达到Pareto最优的分布图和稳定域内Pareto最优解的分布图.可以看到,与Tp=1(图4)的情况相比,系统3个稳定性指标的最优取值范围都扩大了,其中噪声带宽Wn的取值范围从0~4扩大到0~20,扩大倍数比其他2个指标都要大.
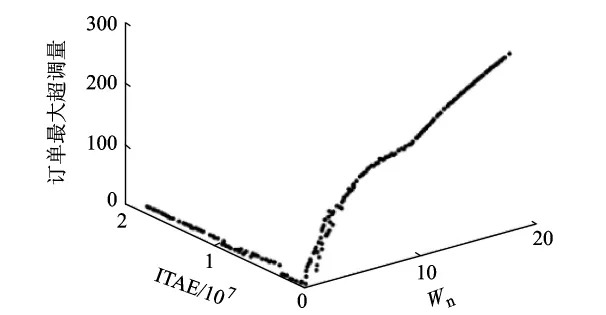
图9 Tp=2时系统稳定性指标订单最大超调量、ITAE、Wn最优时三维分布图
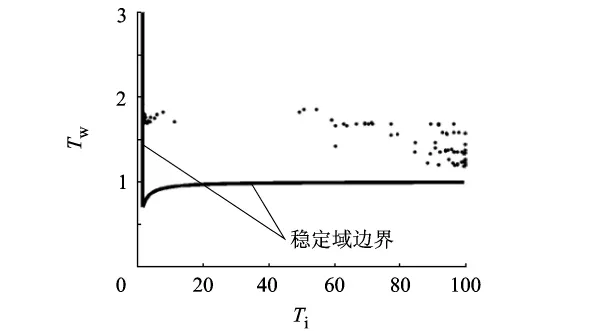
图10 Tp=2时DIS-APIOBPCS系统稳定区域内最优点
图11为需求预测参数Ta对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.与图6的情况类似,2组稳定性指标ITAE和Wn与订单超调量对于Ta仍然表现出完全相反的行为模式.当Ta取值较大时,Wn和订单超调量的值都会被限定在较小的取值范围内,而ITAE的值则相对较大.另一方面,当Ta取值较小时,ITAE的值会变小.由于ITAE随Ta取值不同变化更为剧烈,若企业希望避开ITAE的不利影响,仍然可以使Ta取值更小从而限制ITAE取值.反之,如果企业不希望使Wn与订单超调量过大,则可以取比较大的Ta值以提高供应链运行的稳定性和绩效.
图12为库存调节参数Ti对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.由于与图7的情况类似,此处不再赘述.
图13为在制品调节参数Tw对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.与Tp=1情况下的图8相比,Tw对3个稳定性指标的影响呈现相似的情况,不同之处在于Tw的最优取值范围变小,仅在1.18~1.92的范围内,对比图5(Tw的取值在0~5和15~30范围)和图10(Tw的取值在1~2范围内)亦可得出相同的结论.由于ITAE的一系列最小值都出现于Tw取值较大的一个连续的区域内,因而在这个范围内选取合适的Tw的值可以获得较小的ITAE值.同时,要使Wn与订单超调量的取值不是太大,就要限定Tw在取值较小的一个区间内.根据对图13的分析,可以看出,虽然Tw的取值范围很小,但是企业仍然可以根据系统性能指标的重要性选取对自身最优的Tw的值,从而获得最优性能.
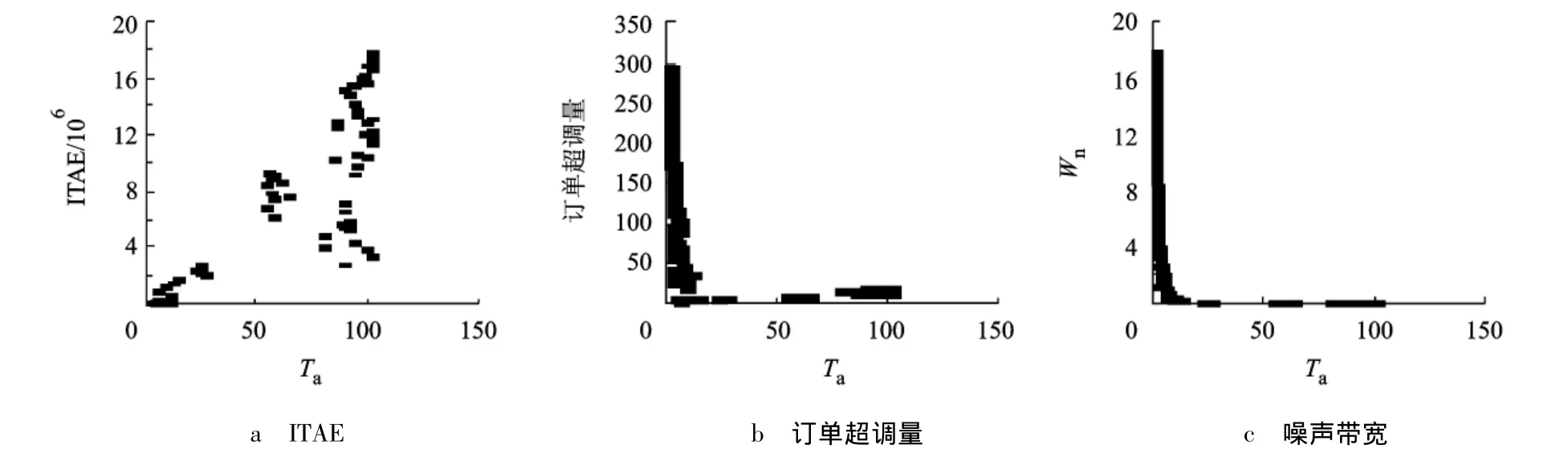
图11 Tp=2时Ta对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
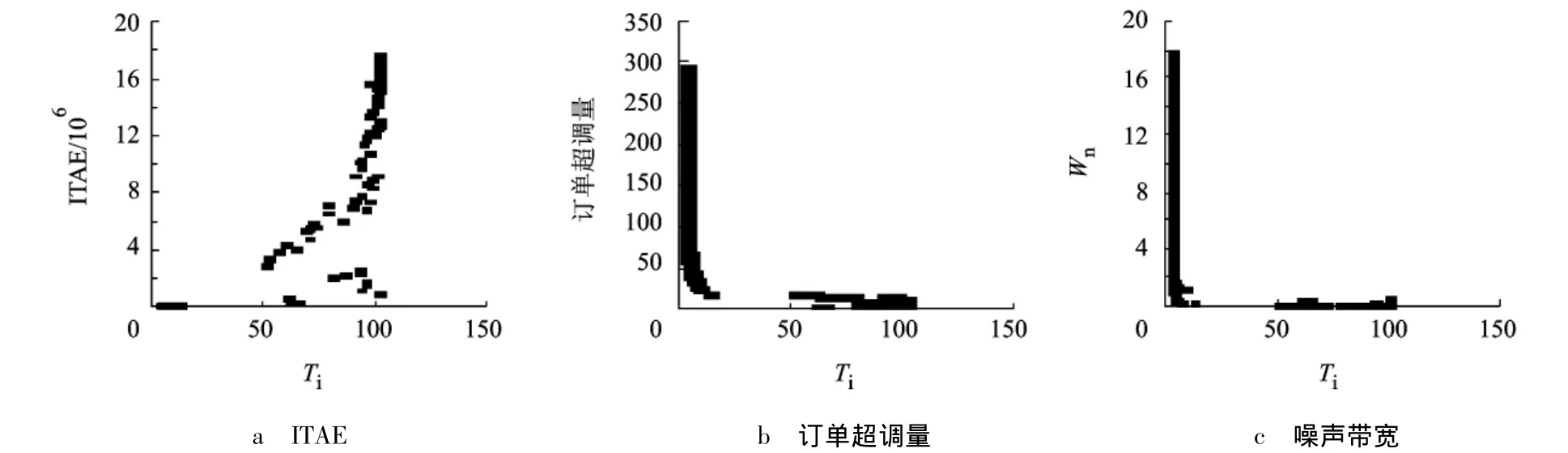
图12 Tp=2时Ti对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
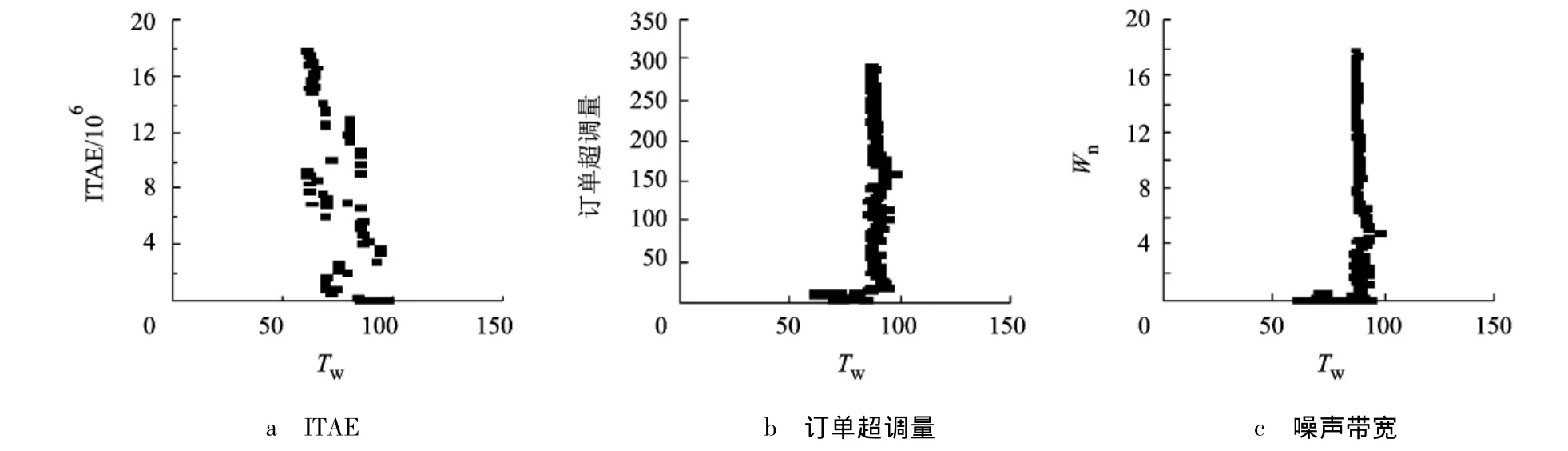
图13 Tp=2时Tw对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
2.3 Tp=3时系统稳定性指标的最优化
提前期参数Tp=3时,系统的稳定性条件[9]为
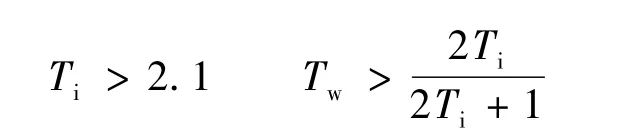
Tp=3情况,稳定域内供应链系统的3个稳定性指标达到Pareto最优的分布图和稳定域内Pareto最优解的分布图如图14、图15所示.与Tp=2情况相比,Wn和订单超调量的取值范围缩小了,但是ITAE的取值范围扩大了.然而与Tp=1情况相比,Tp=3时3个稳定性指标的取值范围都扩大了.比较图5、图1与图15,可以发现,Tp=1与Tp=3两种情况下最优解在稳定域内的分布大致相同,但是Tp=2时参数Tw的取值范围就比前面的两种情况要小.
图16为需求预测参数Ta对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.
图17为库存调节参数Ti对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.对比图16与图6和图11,图17与图7和图12,可以发现,Ta和Ti对系统的3个稳定性指标的影响极为类似,只是在取值上有差异,此处不再赘述.
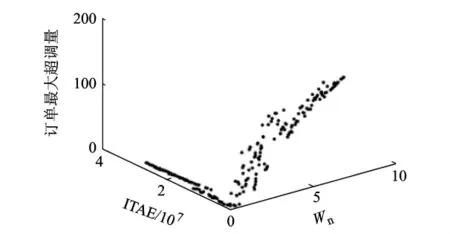
图14 Tp=3时系统稳定性指标订单最大超调量、ITAE、Wn最优时三维分布图
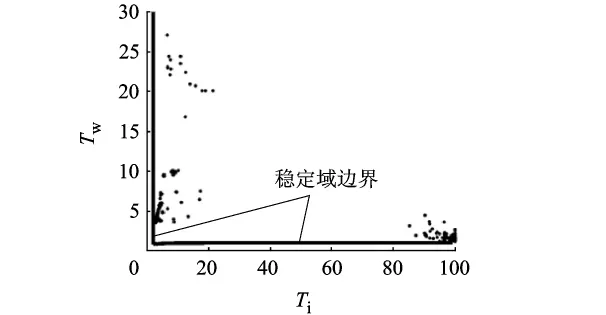
图15 Tp=3时DIS-APIOBPCS系统稳定区域内最优点
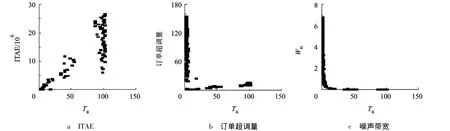
图16 Tp=3时Ta对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
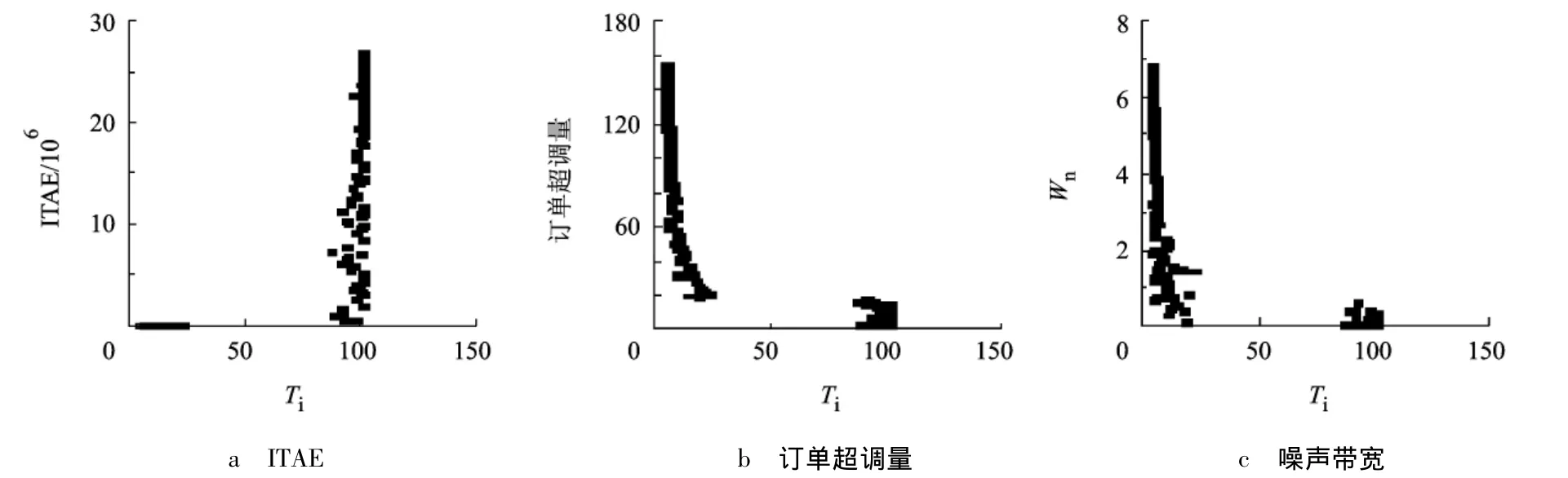
图17 Tp=3时Ti对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响

图18 Tp=3时Tw对最优条件下ITAE、订单超调量、噪声带宽3个性能的影响
图18为在制品调节参数Tw对需求信息共享供应链在Pareto最优状态下的3个稳定性指标的影响.比较图18和图8可以发现当Tp=3时Tw的取值范围与Tp=1时的取值范围相近,与Tp=2时取值范围有很大不同.图18b与图8b和图13b类似,当Tw的取值较大时,ITAE的值相对较小.因此如果企业忽略Wn与订单超调量的影响,而只看重ITAE这个指标,与前面的分析类似,在一个很大的范围内选取合适的Tw的值能使ITAE的取值最小.然而图18a和图18c却表现出与Tp=1,Tp=2两种情况极为不同的影响,Wn与订单超调量不再与Tw成正相关关系,没有明显的规律性.
3 进一步分析
由于上述分析是在供应链系统的3个稳定性指标达到Pareto最优的条件下进行的,为了保证调节某一系统参数时稳定性指标的Pareto最优,系统参数的Pareto最优解组合也发生相应变化.为了得到系统参数对稳定性指标的更一般的影响,本文做了进一步分析.这里分析仅考察单一系统参数变化对3个稳定性指标的影响,并不保证稳定性指标处于Pareto最优范围内.
设定 Tp=1,Ta=5,Tw=12,令 Ti从 1.1 变化到100,通过仿真实验,得到Ti对3个性能指标的影响,如图19和图20所示.图19表明,ITAE随着Ti增大而迅速增大;图20显示了Ti与Wn及订单超调量呈负相关关系.改变参数Tp,Ta,Tw的取值发现Ti与ITAE,Wn及订单超调量的关系仍与图19和图20显示的特征类似,如图21所示.所以通过参数Ti调节系统的稳定性指标时,Wn和订单超调量2个稳定性指标与ITAE表现出相反的行为模式.这与前面分析Ti对Pareto最优条件下3个稳定性指标的影响时得到的结论是一致的,即ITAE和Wn与订单超调量2组指标对于Ti表现出完全相反的行为模式,所以在实际应用中企业需要认真分析各稳定性指标的重要性,调节好Ti的取值以使供应链系统的稳定性达到企业的要求.
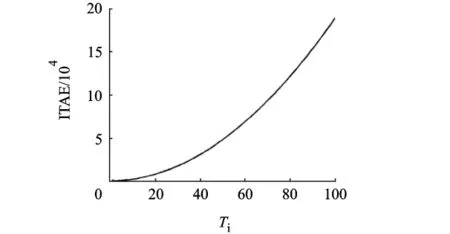
图19 Ta=5时Ti与ITAE关系图
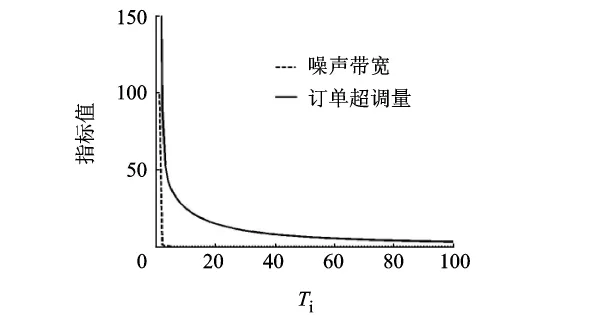
图20 Ta=5时Ti与噪声带宽及订单超调量关系图
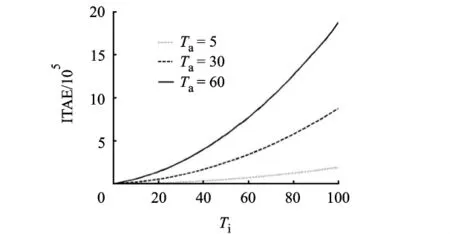
图21 Ti与ITAE关系图
而且通过实验可以发现,需求预测参数Ta与库存调节参数Ti对 ITAE的影响很大,且都与ITAE呈现正相关关系(图21).而在制品调节参数Tw对ITAE的影响很小(图22),这也可以解释为何Pareto最优解中Tw的取值范围比Ta和Ti的取值范围都要小很多.Pareto最优解一般出现在Ta和Ti的取值为0~100的范围内;而 Tw在不同情况下取值范围和影响有所不同,而且比Ta和Ti的取值范围都要小很多,最多在0~40的范围内.通过取定点仿真实验(图2)发现Tw和Wn与订单超调量之间的关系没有明显的规律性.在前面分析Tw对最优条件下3个稳定性指标的影响时(图8,图13,图18),图中显示的 Tw和 Wn与订单超调量之间的关系也没有表现出明显规律性.
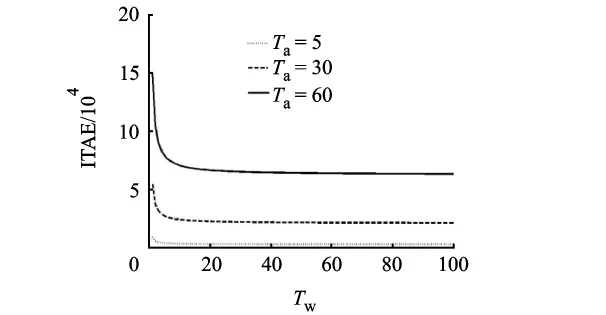
图22 Tw与ITAE关系图
4 结论
本文以需求信息共享的供应链订货系统DIS-APIOBPCS为研究对象,分析模型中涉及到的需求预测参数Ta、库存调节参数Ti、在制品调节参数Tw对系统稳定性的影响,其目的是确定使系统达到全面稳定状态的最优参数组合及不同最优参数组合对系统稳定性指标的影响.本文对供应链系统不同提前期参数Tp取值的情况分别进行了分析.针对反映供应链系统稳定性的3个重要指标对需求信息共享的供应链系统进行优化.由于这是一个多目标优化问题,所以选择了最适合的优化方法NSGA-Ⅱ作为优化工具.本文的思想是在需求信息共享的供应链系统稳定域内对系统进行优化.一方面使系统参数在一定的约束范围内;另一方面是要验证稳定域内的点在系统稳定性特性上并非匀质的假设.对供应链系统输入阶跃需求信号,通过仿真实验搜索系统参数满足3个系统稳定性指标达到Pareto最优条件的Pareto最优解,并得到了稳定域内最优解的分布情况,然后分析了不同系统参数组合对系统最优状态下的稳定性的影响.可以发现在系统Pareto最优状态下,在系统参数变化的影响下,噪声带宽和订单超调量2个稳定性指标与ITAE表现出相反的特征.Pareto最优解一般出现Ta和Ti的取值在0~100的范围内;而Tw在不同情况下取值范围和影响有所不同,而且比Ta和Ti的取值范围都要小很多,最多在0~40的范围内.由于3个供应链系统稳定性指标达到Pareto最优的取值是一个集合,而且系统参数在稳定域范围内的Pareto最优解均能保证供应链系统达到最优,但是并非Pareto最优集合中的每一组供应链系统稳定性指标值都符合企业的实际情况,不具有普适性,因此企业必须对Pareto最优集合中这3个稳定性指标进行权衡.在3个供应链系统稳定值指标中ITAE随3个参数取值不同变化更为剧烈,因此如果企业希望规避ITAE的不利影响,可以通过适当选择参数Ta,Ti,Tw的取值控制 ITAE 取值.通过分析 Ta和Ti对最优状态下3个稳定性指标的影响可以发现,当Ta和Ti取值比较小时,噪声带宽和订单超调量的值都很大,随着Ta和Ti取值变大这2个指标的值就会被限定在一个较小值范围内.如果企业希望获得较小的噪声带宽和订单超调量的值,而忽略ITAE的影响,那么就不应取较大的Ta和Ti值.
References)
[1]Disney S M,Towill D R.A discrete transfer function model to determine the dynamic stability of a vendor managed inventory supply chain[J].International Journal of Production Research,2002,40(1):179 -204
[2]Riddalls C E,Bennett S.The stability of supply chains[J].International Journal of Production Research,2002,40(2):475 -495
[3]Darya Kastsian,Martin Mönnigmann.Optimization of a vendor managed inventory supply chain with guaranteed stability and robustness[J].International Journal of Production Economics,2011,131(2):727 -735
[4]Disney S M,Naim M M,Towill D R.Genetic algorithm optimisation of a class of inventory control systems[J].International Journal of Production Economics,2000,68:259 -278
[5]Disney S M,Towill D R.A procedure for the optimization of the dynamic response of a vendor managed inventory system[J].Computors & Industrial Engineering,2002,43:27 -58
[6]Towill D R.Industrial dynamics modeling of supply chains[J].International Journal of Physical Distribution & Logistics Management,1996,26(2):23 -42
[7]Dejonckheere J,Disney S M,Lambrecht M R,et al.The impact of information enrichment on the bullwhip effect in supply chains:a control engineering perspective[J].European Journal of Operational Research,2004,153(3):727 -750
[8]Ou Y,Yan F.The effect of information sharing on supply chain stability and the bullwhip effect[J].European Journal of Operational Research,2007,182(3):1107 -1121
[9]王晶,唐玲,王寻.需求信息共享供应链系统的稳定性分析[J].北京航空航天大学学报,2009,35(8):1009 -1012 Wang Jing,Tang Ling,Wang Xun.Stability analyses of demand information sharing supply chain systems[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(8):1009-1012(in Chinese)

