基于数字电视信号处理中有关数字滤波器的设计

山东省广播电影电视局蒙山转播台 高 峰

1.IIR数字滤波器的设计

1.1 IIR数字滤波器的传统设计方法

IIR数字滤波器具有无限宽的冲击相应，与模拟滤波器相匹配。所以IIR滤波器的设计可以采取在模拟滤波器设计的基础上进一步变换的方法。例如：

利用脉冲响应不变法设计IIR数字滤波器，其基本设计思路是直接设计一个数字滤波器并让它的时间特性逼近一个模拟滤波器。为了达到时间特性的最佳逼近，把模拟滤波器的冲击响应均匀取值，作为数字滤波器的单位脉冲响应，即：

h(n)=h(t)∣t-nT

然后将h(n)通过z变换即求得H(z)。因此，脉冲响应不变法实际是时域取样法，整个过程是先根据给定的指标设计一个模拟滤波器，进而按下列变换的顺序，最后求得数字滤波器的系统函数H(z)，即：

H(s)→h(t)→h(n)→H(z)

在对滤波器进行实际设计时，整个过程运算量是很大的。设计完成后要对已设计的滤波器的频率响应进行校核，得到幅频相频响应特性，运算量也是很大的。通常，待设计的数字滤波器，阶数和类型并不一定是完全给定的，很多时候都是要根据设计要求和滤波效果不断进行调整，以达到设计的最优化。在这种情况下，滤波器的设计就要进行大量复杂的运算，单纯的靠公式计算和编制简单的程序很难在短时间内完成设计。利用MATLAB强大的计算功能进行计算机辅助设计，可以快速有效地设计数字滤波器，大大地简化了计算量，直观简便。

表1 5种窗函数性能比较

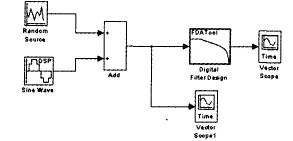
图1 IIR数字滤波器仿真图

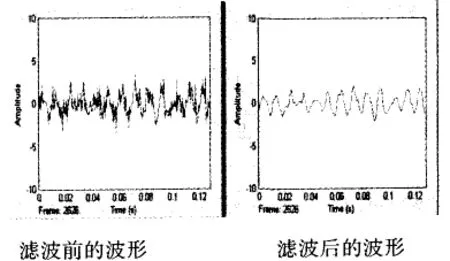
图2 滤波前和滤波后的波形图

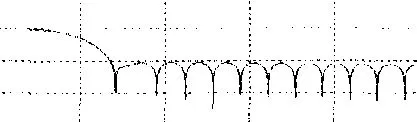
图3 利用窗函数实现的FIR数字滤波器

1.2 IIR数字滤波器的MATLAB设计

应用实例：设计通带截止频率为500Hz、阻带截止频率为600Hz、通带的最大衰减为ldB、阻带的最小衰减为50dB、采样频率为2000Hz的数字低通巴特沃斯滤波器。

(1)程序设计法

在MATLAB中，对各种滤波器的设计都有相应的计算振幅响应的函数，可以用来做滤波器的程序设计。对于上面的应用实例，也可以采用程序设计法利用模拟巴特沃斯滤波器来实现数字低通滤波器的设计。在前面已经介绍了脉冲响应不变法设计IIR数字滤波器的原理和函数的转换方法，下面给出采用脉冲响应不变法实现IIR数字低通滤波器设计的部分代码：

%利用模拟巴特沃斯滤波器设计数字低通滤波器

%脉冲响应不变法

Wp=500；%Wp为通带截止频率

Ws=600；%Ws为阻带截止频率

Rp=1；%Rp为通带w(=0一Wp)中的最大衰减系数

As=50；%As为阻带W>=Ws中的最小衰减系数

Fs=2000；%Fs为采样频率%性能指标

OmgP=2*pi*Wp：

OmgS=2*pi*Ws：

[N,OmsC]=buttord(Omgp,OmsS,Rp,As,’s’)；%选取模拟滤波器的阶数

[cs,ds]=butter(N,OmgC,’s’)；%设计出所需的模拟低通滤波器

[bz,az]=impinvar(cs,ds,Fs)；%应用脉冲响应不变法把模拟滤波器转换为数字滤波器

(2)Simulink仿真

Simulink是MATLA B软件的扩展，是一个实现动态系统建模和仿真的软件包。它与MATLAB语言的主要区别在于：Simulink与用户交互接口是基于Windows的模型化图形输入，因而用户可以把更多的精力投入到系统模型的构建，而非语言的编程上。所谓模型化图形输入是指Simulink提供了一些按功能分类的基本的系统模块，用户只需要知道这些模块的输入输出及模块的功能，而不必考察模块内部是如何实现的，通过对这些基本模块的调用，再将它们连接起来就可以构成所需要的系统模型，进而进行仿真与分析。下面介绍如何调用Simulink中的功能模块来实现IIR数字滤波器仿真的方法，在仿真过程中，可以双击各功能模块，随时改变参数，以便获取不同状态下的仿真结果。

本次设计是对带有白噪音的正弦波信号进行滤波处理，调用Simulink中的功能模块构成数字滤波器的仿真框图，如图1所示。在图2中，应用了Simulink环境中的Signal Processing Blockset工具箱。该工具箱提供了一些滤波器模型，在设计时通过设置相应的参数即可得到需要的数字滤波器模型。对于输入信号，通过DSPSources模块中的一个白噪音信号模块RandomSource和一个正弦波信号模块Sine Wave，叠加在一起形成一个带有干扰信号的杂质波。对于滤波器的设计，通过Filter Designs模块中的Digital Filter Design模块设计符合要求的低通滤波器，对带有干扰的原始信号进行滤波。

此外，图2中还有两个信号输出模块，分别应用DSP Sinks模块中的Vector Scope模块输出滤波前和滤波后的波形图，Vector Scopel用来输出带有干扰的原始信号，Vector Scope用来输出经滤波器滤波之后的信号，以便在仿真运行的过程中可以动态地观察滤波效果。例如在滤波器设计模块中设置2阶低通IIR数字滤波器，采样频率为1000Hz。仿真运行后的结果如图3所示。从图3中可以看到，该数字滤波器仿真模型实现了对原始信号进行动态数字滤波的功能，滤除了原始波中的忙刺，得到了很好的正弦波信号，在数字信号传输和处理过程中对信号杂质作了清除，达到了滤波器的设计要求。

利用MATLAB的强大运算功能，应用基于MATLAB的IIR数字滤波器设计方法可以快速有效地实现由软件组成的常规IIR数字滤波器的仿真，设计方便、快捷，极大地减轻了工作量，在设计过程中还可以对比滤波器特性，随时更改参数，以达到滤波器设计的最优化，为滤波器的设计和实现开辟了广阔的天地。

2.FIR数字滤波器设计

2.1 窗函数法

窗函数是一种用一定宽度窗函数截取无限长脉冲响应序列获取有限长脉冲响应序列的设计方法。而其设计FIR滤波器的基本思想：根据给定的滤波器技术指标选取滤波器长度N和窗函数Wd(n)，使其具有最窄宽度的主瓣和最小的旁瓣。其核心是从给定的频率特性。通过加窗确定有限长单位脉冲响应序列h(n)即实际滤波器的系数向量。其是由理想滤波器脉冲响应hd(n)与窗函数函数Wd(n)相乘得到。工程上常用的窗函数有5种。即矩形窗（Rectangular Window）、三角形窗(Triangular Window)、汉宁窗(Harming)、哈明窗(Hamming)-凯泽窗(Kaiaser-Bassel Window)。它们之间的性能比较如表1所示。为了满足工程上需要，可以通过改变窗函数的形状来改善滤波器的幅度频率特性。窗函数的选择原则是：

(1)具有较低的旁瓣幅度，尤其是第一旁瓣的幅度；

(2)旁瓣的幅度下降的速率要快，有利于增加阻带衰减；

(3)主瓣的宽度要窄，这样可以得到较窄的速度带。

通常以上几种难以同时满足。实际中选用的窗函数往往是它们的折中。

2.2 利用窗函数进行数字滤波器设计示例

用Hamming窗设计一个线性相位低通FIR数字滤波器，截止频率wc=0.2*pi。窗口长度N15，33.要求在两种窗口长度下，分别画出h(n)和响应幅频特性和相频特性的变化，注意长度N变化的影响。程序如下：

N=15;wc=0.2*pi;

b=fir1(N，wc/pi);

[H，W]=freqz(b，1)

mag=abs(H);db=20*log10((mag+eps)/max(mag));

subplot(2，1，1);

plot(W/pi，db);grid;

xlabel(‘频率、Hz’);ylabel(‘幅值’)；

subplot(2，1，2);

plot(W/pi，unwrap(angle(H)));grid;

xlabel(‘频率/Hz’);ylabel(‘相位’)；

通过以上程序可得出图像如图3。

一般DSP芯片实现FIR滤波器时，常是先在Matlab中设计要求的滤波器，得到滤波器系数，在目标DSP汇编程序中，对系数进行相应的Q格式转换，再用相关汇编指令实现FIR滤波器算法。但在调试时，每改变一次滤波器参数，相关系数也改变，目标DSP中的程序也要做相应改变，给调试仿真带来很大麻烦，使滤波器设计效率很低。Matlab具有强大的数值分析、计算、信号处理及图形显示功能，并为用户提供了强大的信号处理工具箱和友好方便的交互式图形用户界面，用Matlab辅助DSP实现FIR，在滤波器系数改变时可以不必改变DSP中程序，大大提高了滤波器设计效率。本文只是利用Matlab辅助DSP实现了一个简单的FIR低通滤波器，并在TMS320C6713 DSK上成功运行。还可以利用Matlab辅助DSP来实现比较复杂的诸如语音处理、通信、图像处理等方面的程序开发，可以大大缩短DSP应用程序的开发时间，提高设计效率，这也是以后DSP设计的一个趋势。

3.结束语

通过对上面内容的介绍我们可以清楚的认识到Matlab在数字信号处理中的应用。具体可体现为：在离散系统中的分析，IIR数字滤波器中的设计，FIR数字信号处理中的应用等方面。以后的数字信号处理课程在Matlab软件的作用下会更好的利于应用。Matlab已经给数字信号处理课程带来了一次变革，以后会更能体现出其在数字信号处理中的应用。

[1]王艳芬,史良,王刚.基于Matlab软件环境的“数字信号处理”课程新实验开发[J].实验技术与管理,2002,19(3).

[2]丁玉美,高西全.数字信号处理[M].西安:电子科技大学出版社,2001(第2版).

[3]伯晓晨,李涛,刘路,等.Matlab工具箱应用指南——信息工程篇[M].北京:电子工业出版社,2000.

[4]刘云秀,李晓光,基于MATLAB语言数字FIR.滤波器的设计[J].吉林师范工程技术学院学报,2003,20(3):26-28.

[5]胡锦,彭成,孙晓宁.FIR数字滤波器的优化设计[J].宇航计测技术,2006,26(6):48-51.

[6]陈怀深,吴大正,高西全.Matlab及在电子信息课程中的应用[M].北京:电子工业出版社,2004.