线性Radon变换噪音压制法及其在古龙断陷中的应用
石 颖,李 莹,王维红,陆加敏
(1.东北石油大学 地球科学学院,黑龙江 大庆 163318; 2.大庆油田有限责任公司 勘探开发研究院,黑龙江 大庆163712)
线性Radon变换噪音压制法及其在古龙断陷中的应用
石 颖1,李 莹1,王维红2,陆加敏2
(1.东北石油大学 地球科学学院,黑龙江 大庆 163318; 2.大庆油田有限责任公司 勘探开发研究院,黑龙江 大庆163712)
针对松辽盆地北部古龙断陷地震资料信噪比低、线性干扰强特点,提出应用线性Radon变换进行叠前线性噪音压制的预处理方法,Radon变换可在炮集和CMP道集上进行运算,算法简单,易于编程实现,其积分路径的特点适合线性噪音压制.模拟数据和实际地震资料应用结果表明,线性Radon变换法能够实现保幅的线性噪音压制,是叠前提高地震资料信噪比的实用方法,在地震资料预处理中具有应用前景.
Radon变换;线性噪音;压制;信噪比;古龙断陷;地震资料
0 引言
当前油气勘探以复杂构造和岩性油气藏为主,要求高保真和高信噪比的地震成果数据体,以利于进行综合地质研究和勘探部署.地震资料噪音主要包括随机噪音和规则噪音两类,其中规则噪音中的线性噪音在地震资料中普遍存在,往往具有较强的能量,所以线性噪音压制效果在一定程度上决定着成像数据体质量[].
根据有效信号与线性噪声的特征差异,研究并提出了不同的线性噪音压制方法,主要包括F-K滤波法、径向滤波法、K-L变换法和Radon变换法等[2-6].其中F-K滤波法是频率域方法,易于实现;但是在有效波和线性干扰之间的视速度相近时,难以有效实现有效波和噪音的分离.径向滤波法根据选定的线性同相轴的视速度和滤波的径向道数,实现线性干扰的压制;但是该方法需要过多的人为参与,对于海量地震数据处理,计算效率低,计算结果在很大程度上取决于滤波道数的选择,且地震数据体中往往有较多的残余噪音.K-L变换法是基于目标统计特征的正交变换,能够实现随机噪音、线性噪音和多次波等规则噪音压制;但是该方法噪音压制效果取决于本征值选择,本征值选择需要反复的数值试验,若本征值选择不当将造成噪音的大量剩余,同时有效波的信号也受到一定的损失.
线性Radon变换法算法简单,在地震资料处理中被广泛应用,如资料预处理中的线性噪音压制、地震数据的插值和重建、VSP资料处理中的波场分离和叠前偏移领域等[6-9].线性Radon变换法能够较好地实现有效波和相干线性噪音的分离,计算效率高,线性同相轴在Radon正变换域可变换为点,滤波函数简单,同时经噪音模型反变换后,从原始数据中将线性噪音减去,对有效波的振幅没有任何伤害,是一种高效的相对保幅的线性噪音压制技术[10-12].依据线性Radon变换原理,对大庆油田古龙断陷区的地震资料进行强线性干扰压制,获得良好成像效果,试算结果表明算法具有计算效率高、精度高和实用性强的特点.
1 Radon变换原理与实现
对于二维地震资料,假设沿偏移距方向为均匀采样,则离散线性Radon正变换[9,13]可以写为
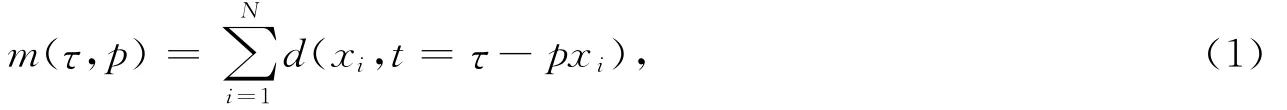
式中:d(xi,t)为x-t域地震数据体,共有N 道数据,xi为偏移距;m(τ,p)为Radon正变换域数据体,τ为地震数据中零偏移距道对应的截距时间;p为射线参数.
对Radon变换的离散公式(1)两端进行Fourier变换,对任一频率分量进行计算[9,11]:

式中:M(p,ω),D(xi,ω)分别为m(τ,p)和d(xi,t)相对应的Fourier变换域的表示形式.将方程(2)写成矩阵形式:

式中:d为时间空间域地震数据矩阵;m为Radon域矩阵;L为数据变换矩阵,L中的元素可表示为

一般来说,方程(3)是欠定或超定的,采用最小二乘方法求其最优解,其一般形式为

式中:LH为矩阵L的共轭转置;m,d分别为模型空间(Radon正变换域)和数据空间(时间空间域)的任一频率成分的向量.
式(5)和式(3)共同构成线性Radon正反变换对.在离散计算时,Radon变换进行参数的合理采样.线性Radon变换的参数τ和时间域的参数t的采样相等,其射线参数p的采样间隔Δp为

最大射线参数pmax的表达式为

式(6-7)中:fmax为地震资料的最大有效频率;Xmax为原始数据单炮或CMP道集的最大偏移距;Δx为道集中的道间距[14].
线性Radon变换求解方法是矩阵求逆,式(5)可能是超定方程(未知数个数少于方程个数),也可能是欠定方程(未知数个数多于方程个数),对于文中线性噪音压制问题,单个频率成分所形成的矩阵为Toeplitz矩阵,可以应用共轭梯度法、Cholesky分解法或Levinson递推法进行求解,其中Levinson递推算法的计算效率最高[13].
2 模拟数据试验
为验证Radon变换线性噪音压制方法的有效性,应用理论模拟的单炮数据进行噪音压制试算.数值模拟含一个有效波同相轴和一个线性同相轴的单炮数据(见图1(a)).由图1(a)可以看出,模拟线性噪音的能量很强.模拟采用主频为20 Hz的Ricker子波,共84道地震记录,地震道采样间隔为40 m,时间方向采样间隔为4 ms,最大偏移距为3 320 m.采用式(5)计算最小二乘Radon域的正变换域见图1(b).由图1(b)可以看出,模拟炮记录中线性同相轴在线性Radon正变换域表现为相对聚焦的剪刀状特征,而有效波表现为椭圆形式.在Radon正变换的模型空间域设计滤波函数,可以容易地滤除点状形式的线性同相轴,将滤波的结果进行反变换,即可得到线性同相轴(见图1(c)),将图1(c)从原始地震数据中减去,得到线性噪音压制后的结果剖面(见图1(d)).因此,线性Radon变换法可以有效压制地震数据中的线性同相轴.
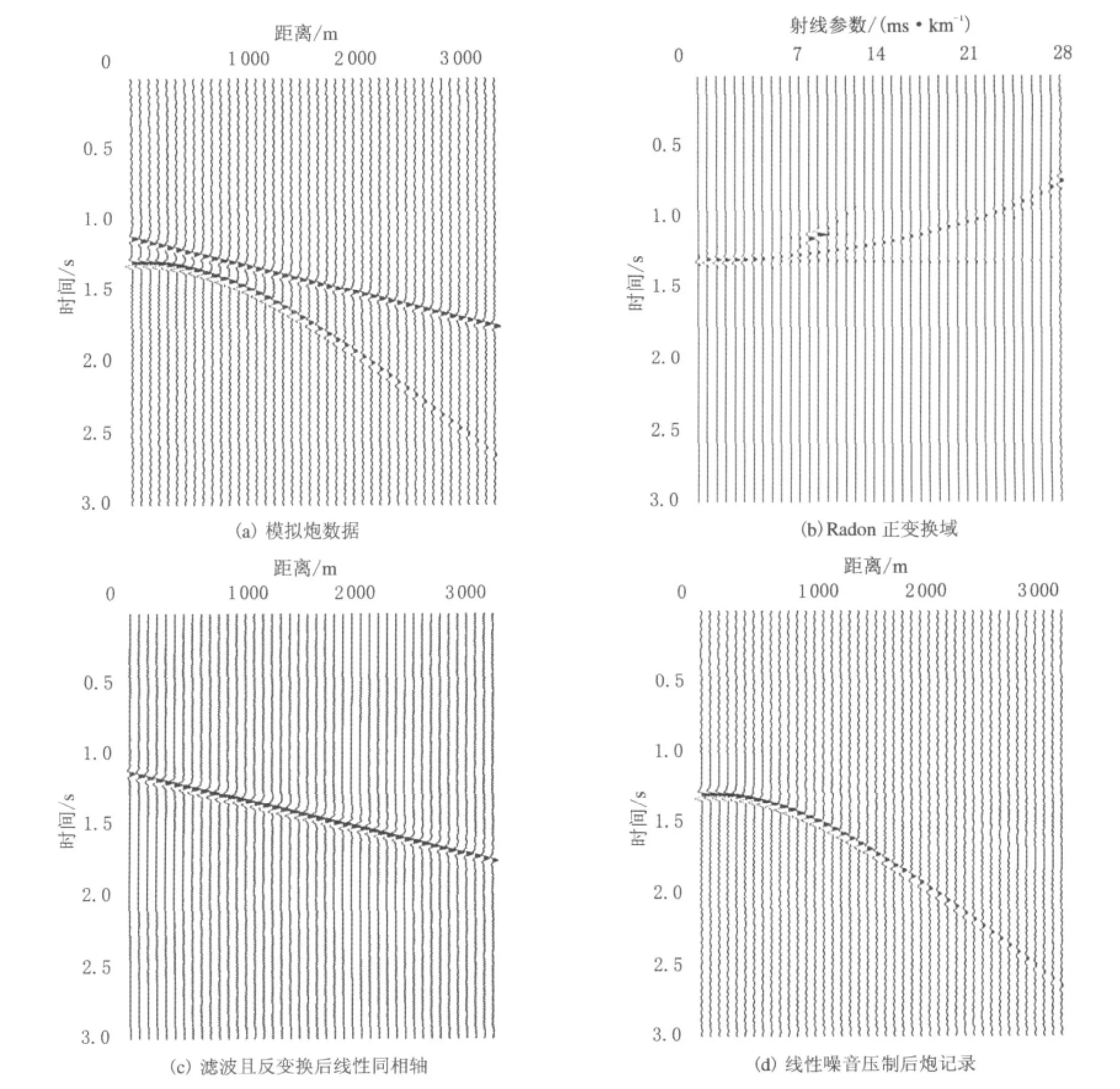
图1 Radon变换线性噪音压制模拟数据试验
线性Radon变换法的基本思想是对某个函数在给定的线性路径上进行积分运算,基于平面波分解原理,也考虑地震波场的性质.根据线性Radon域的特点,可以设计滤波器,在Radon正变换域滤波,以切除不需要的同相轴或者相干噪音,进而大幅提高地震资料的信噪比,表明Radon变换法在线性噪音压制计算中的有效性和实用性.
3 现场资料应用
松辽盆地北部深层天然气勘探在徐家围子断陷取得成功,获得储量的巨大发现[15],当前大庆油田探区的古龙断陷是重要的储量接替区.该区针对深层火山岩勘探的研究程度相对较低,其中影响因素主要包括火山岩目的层埋藏深、地震资料品质差和信噪比低等.为提高古龙断陷深层复杂构造和复杂地质体的成像精度,采用Kirchhoff积分的叠前深度偏移技术[16].该技术要求输入信噪比高的叠前预处理数据体,所以叠前精细噪音压制是提高成像精度的关键环节.
以古龙断陷的葡南工区为例,原始地震资料分析表明,该地区地表条件复杂,折射干扰严重,发育两组折射波,速度分别为1 750 m/s和2 200 m/s.线性噪音具有高能量、强振幅和分布范围广的特点,且有较强的规律性.全区测线或多或少含有这种干扰,几乎分布于整个单炮记录,从而掩盖有效波组.一般而言,根据线性干扰与有效波在速度、频率、时空上的差别,进行线性干扰的识别和压制.在古龙断陷区,线性干扰波具有相对稳定的视速度,所以可以应用线性Radon变换法实现线性干扰的有效压制.另外,在实现过程中同时采用噪音压制的减去法,使得有效波的保幅性得到很大程度的增强.
Radon变换法线性干扰压制前后的单炮效果见图2.由图2(a)可以看出,线性噪音呈排状自上而下分布,几乎掩盖所有的有效波;由图2(b)可以看出,压制干扰后的炮记录较为清晰地显示抛物线型的有效波同相轴,单炮记录的信噪比得到提高;由图2(c)可以看出,该方法能够有效压制古龙断陷的强能量线性噪音,同时有效波的振幅不受损失,即文中方法具有很好的保幅效果.
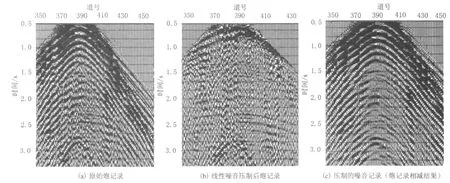
图2 线性干扰压制前后炮记录对比
线性干扰压制前后叠加剖面的效果见图3.由图3可以看出,经过线性噪音压制后,地震剖面信噪比明显提高.通过图2和图3的对比,无论是从单炮还是从叠加剖面都可以看出,线性干扰得到有效压制,突出有效波能量,地震资料的信噪比大幅提高,为叠前深度偏移成像提供资料保障.古龙断陷的实际地震资料线性噪音压制表明,文中Radon变换法具有很强的实用性,能够在信噪比低的同类地震资料处理中推广应用.
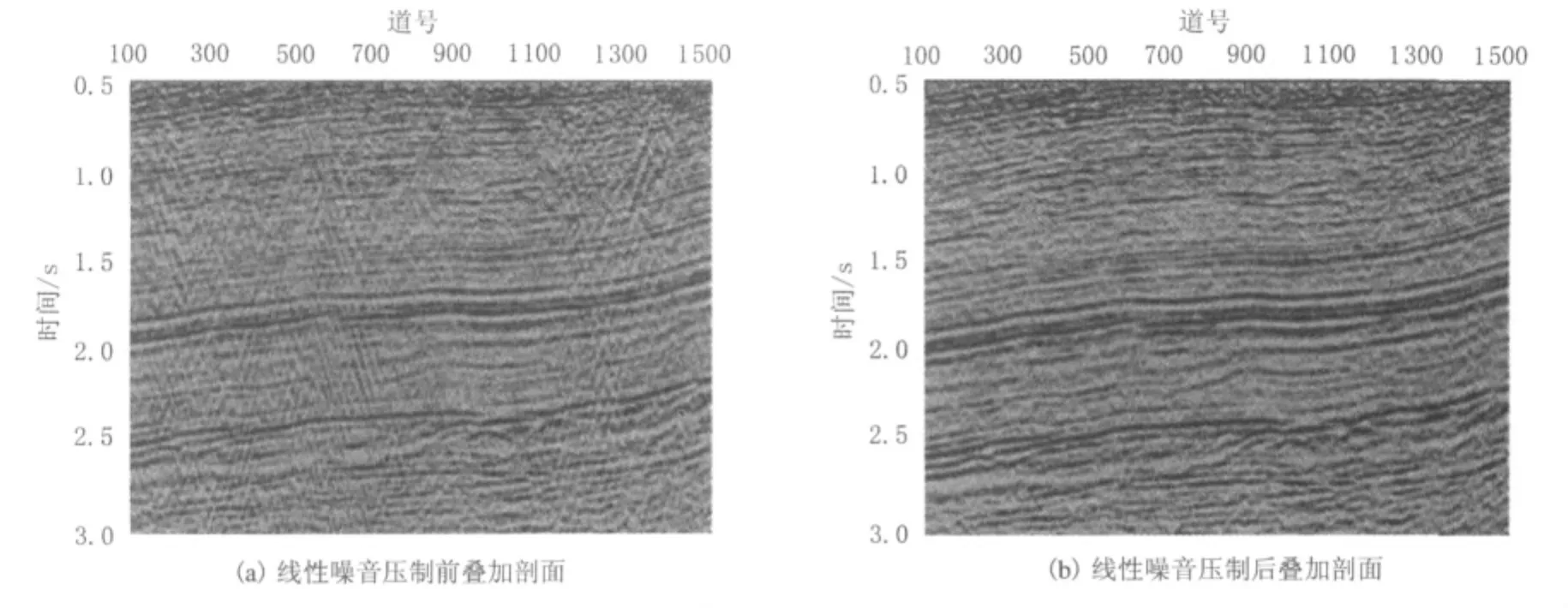
图3 线性干扰压制前后叠加剖面对比
4 结论
(1)线性Radon变换法是对给定函数沿一定路径的积分计算,实际上也考虑地震波场的性质,其变换形式可从平面波分解的原理进行求解和推导.线性Radon变换原理简单,在地震资料预处理中应用广泛.
(2)线性Radon变换法能够较好地实现有效波和相干线性噪音的分离.该方法计算效率高,可以用于炮集或CMP道集数据,线性同相轴在Radon正变换域可变换为点,滤波函数简单,同时经噪音模型反变换后,从原始数据中减去,能够实现线性噪音的保幅压制.
(3)松辽盆地古龙断陷地震资料的线性噪音较为发育,在部分炮记录上具有很强的能量,应用线性Radon变换法进行线性噪音压制,实际地震数据线性噪音压制结果表明,文中给出的线性噪音压制方法具有有效性和实用性,对后续地震波精确成像具有指导意义.
[1]胡天跃.地震资料叠前去噪技术的现状与未来[J].地球物理学进展,2002,17(2):35-40.
[2]闫立志,景新义,李刚.F-K滤波在噪音减去法中的应用[J].海洋地质动态,2006,22(10):28-32.
[3]余波,黄中玉,谈大龙,等.径向道滤波法去线性干扰[J].石油物探,2005,44(2):109-112.
[4]黄雪继,刘来祥,王永胜.分频径向道中值滤波在地震资料处理中的应用[J].物探与化探,2012,36(2):317-320.
[5]刘洪林,张春堂,朱秋影,等.K-L变换在地震资料去噪中的应用[J].大庆石油学院学报,2007,31(4):19-21.
[6]吴律,武克奋,孙立.变换方法及其在地震资料处理中的应用[J].石油物探,1996,1(1):37-52.
[7]Kabir M N,Verschuur D J.Restoration of missing offsets by parabolic Radon transform[J].Geophys.Prosp.,1995,43:347-368.
[8]王维红,刘洪.抛物 Radon变换法近偏移距波场外推[J].地球物理学进展,2005,20(2):289-293.
[9]Schultz P S,Claerbout J F.Velocity estimation and downward continuation by wavefront synthesis[J].Geophysics,1978,43(3):691-714.
[10]林文,魏大力,王建民,等.Radon变换多次波压制方法及应用研究[J].物探化探计算技术,2009,31(4):344-348.
[11]王维红,首皓,刘洪,等.线性同相轴波场分离的高分辨率τ-p变换法[J].地球物理学进展,2006,21(1):74-78.
[12]Cambois G.Preserved amplitude processing in the presence of noise[C].66th Annual Internat.Mtg.,Soc.Expl.Geophys.,SEG Expanded Abstracts,1996:1595-1598.
[13]Kostov C.Toeplitz structure in slant-stack inversion[C].60th Annual Internat.Mtg.,Soc.Expl.Geophys.,SEG Expanded Abstracts,1990:1618-1621.
[14]张旭东.几种多次波压制方法讨论[J].内蒙古石油化工,2011(1):84-85.
[15]胡明,迟建功,吕延防,等.徐家围子断陷徐深21区块盖层封闭能力演化与天然气成藏的关系[J].大庆石油学院学报,2010,34(1):24-28.
[16]王维红,林春华,陈志德,等.古龙断陷深层火山岩地震资料成像方法及应用研究[J].地球物理学报,2011,54(2):310-319.
Prestack reverse time migration based on GPU parallel accelerating algorithm/2012,36(4):111-115
SHI Ying1,LU Jia-min2,KE Xuan1,TIAN Dong-sheng1,WANG Fei3
(1.School of Geosciences,Northeast Petroleum University,Daqing,Heilongjiang 163318,China;2.Exploration and Development Research Institute,Daqing Oilfield Co.Ltd.,Daqing,Heilongjiang 163712,China;3.School of Earth Science,China Petroleum University (Beijing),Beijing 102200,China)
In order to improve the complex subsurface imaging accuracy and computational efficiency of the algorithm,this paper presents an algorithm of prestack reverse time migration based on GPU(Graphic Processing Unit)accelerating which can image the underground complex structure effectively and accurately.By two-way wave equation to calculate wave field extrapolation,prestack reverse-time migration can overcome the dip limit,and the imaging algorithm is performed by high order finite difference in the paper.Wave field extrapolation and imaging condition are calculated by GPU parallel accelerating technology,comparing to conventional algorithm,its computation efficiency has been greatly improved,and it meets large amount of computation requirement in prestack reverse-time migration.The random boundary condition approach is adopted to obtain wavefield information,which reduces the memory demand but sacrifices the computation cost,and it solves the massy memory problem in reverse time migration.The tests on model illustrate that this approach can imaging complicated geological body efficiently and precisely.
reverse time migration;GPU;acceleration;high order finite difference;random boundary condition;complicated structure
TE132.1
A
2095-4107(2012)04-0116-05
DOI 10.3969/j.issn.2095-4107.2012.04.021
2012-05-07;编辑:任志平
国家自然科学基金青年基金项目(41104088,41004057);国家“863”高技术研究发展计划项目(2012AA061202);中国博士后科学基金项目(2011M501009);中国石油科技创新基金项目(2011D-5006-0304);黑龙江省教育厅科学技术研究项目(12511025);黑龙江省博士后科学基金项目(LBH-Z11272)
石 颖(1976-),女,博士,副教授,主要从事地震资料处理方面的研究.

