考虑淬火残余应力铝合金厚板中椭圆裂纹Ⅰ型强度因子计算

丁华锋，朱才朝，李大峰，杜雪松，刘明勇

(重庆大学 机械传动国家重点实验室，重庆 400044)

高强度铝合金预拉伸板是现代航空航天、武器装备工业必不可少的关键材料[1]，其中铝合金厚板作为关键性的结构材料，使用范围广泛。然而铝合金厚板淬火后会产生很大的残余应力[2]，需要进行拉伸等工艺来消除或减小淬火残余应力。如果铝合金板材中存在裂纹等缺陷，在预拉伸过程中常常会发生断带，造成对拉伸机的损伤或破坏，影响其使用寿命。故需要在厚板预拉伸工艺前对铝合金板材进行探伤检测，目前，探伤时都未考虑不同厚度板材的淬火残余应力的影响，按经验设定裂纹等缺陷允许值。对于裂纹这样的缺陷，应力强度因子(K)是裂纹尖端附近的应力状态一个重要表征参量。要准确地预测铝合金板材在预拉伸时断带的临界裂纹尺寸，需要对其在复杂应力场中的应力强度因子进行精确的计算。

工程结构中，椭圆裂纹是最为常见的一种裂纹。这类裂纹应力强度因子的计算通常基于简单的纯拉伸或弯曲载荷，NEWMAN和RAJU[3]计算椭圆裂纹在纯拉伸和弯曲载荷下的应力强度因子。SHIRATORI和MIYOSHI[4]计算了裂纹表面应力分别为均匀、线性、抛物线和立方分布的应力强度因子。1970—1972年，BUECKNER[5]和 RICE[6]提出的权函数法是解决复杂边界和载荷条件下的裂纹应力强度因子的有效方法，之后有众多学者对不同裂纹的权函数进行了深入的研究[7-9]。GLINKA 等[10-12]进一步发展了一种普遍适用的权函数，并应用于计算半椭圆裂纹、角裂纹的应力强度因子。LAMMI和LADOS[13]研究了结构材料在动载荷条件下，残余应力对疲劳裂纹扩展的影响。2010年，BAO等[14]用权函数法和有限元法分别计算了考虑焊接应力的裂纹应力强度因子，计算结果表明，焊接应力对结构承载能力有较大的影响。

由于淬火残余应力对铝合金板中裂纹的应力强度因子有较大影响，尤其是厚板淬火后会产生很大的残余应力，在计算铝合金板材预拉伸时的应力强度因子，不能忽略淬火残余应力的影响。对于淬火残余应力场中裂纹应力强度因子的计算，国内外还鲜有研究。本文作者采用 Shen-Glinka法确定残余应力场中裂纹的Ⅰ型应力强度因子权函数(KI)，推导出裂纹的残余应力强度因子。

1 淬火残余应力的分布

对铝合金淬火残余应力的分布已有很多学者做过大量研究，研究结果表明[15-16]，淬火残余应力厚度方向的残余应力远小于长度方向和宽度方向残余应力的，故厚度方向的残余应力可以忽略不计。淬火残余应力沿板材厚度呈“外压内拉”型分布[2]，从外至内由压应力逐渐过渡为拉应力，这一过渡为非单调的连续变化，且沿板材中心面呈对称分布。预拉伸时，铝合金板材承受的载荷为拉应力，故可只考虑长度方向的残余应力，不考虑宽度方向的残余应力，研究裂纹的Ⅰ型应力强度因子。淬火残余应力分布具有对称性，可沿铝合金板材厚度方向取一半建立表面半椭圆裂纹模型，板材的长、宽、厚分别为H、W、t，如图1所示，其中椭圆裂纹的长轴为2c，短轴长为2a。只考虑z方向的淬火残余应力。

为计算z向淬火残余应力场中的裂纹应力强度因子，需要得到淬火残余应力的分布函数。根据已有实验测试和数值模拟结果[1-2]，将数据归一化，铝合金板的残余应力在厚度方向上呈对称分布，淬火残余应力沿图1中y方向分布如图2所示，可将z向残余应力分布拟合成以下函数：

图1 铝合金板半椭圆裂纹模型Fig.1 Semi-elliptical cracks model of aluminum alloy plate

图2 残余应力沿厚度方向的分布Fig.2 Residual stress distribution along thickness direction

式中：σ0为最大应力值。

2 考虑残余应力的权函数法

虽然已有很多学者对各种应力强度因子进行了广泛的研究[17-18]，但对于残余应力场中的应力强度因子的计算，权函数法无疑是一种最有效的方法，应力强度因子K可表示为

式中：a为裂纹深度；(yσ)为无裂纹体中假想裂纹处的应力分布； ),(aym为对应的权函数。

上式表明，在任意裂纹面载荷)(yσ作用下，只要知道了该裂纹的权函数),(aym，则对应的应力强度因子可以通过积分求得。对于半椭圆表面裂纹，裂纹最深处A点和表面B点的应力强度因子最为重要，故只计算此两点的应力强度因子。对于KI的计算，SHEN和GLINKA[11]提出一种普遍适用的权函数法，裂纹最深处A点的权函数(mA(y,a))可表示为

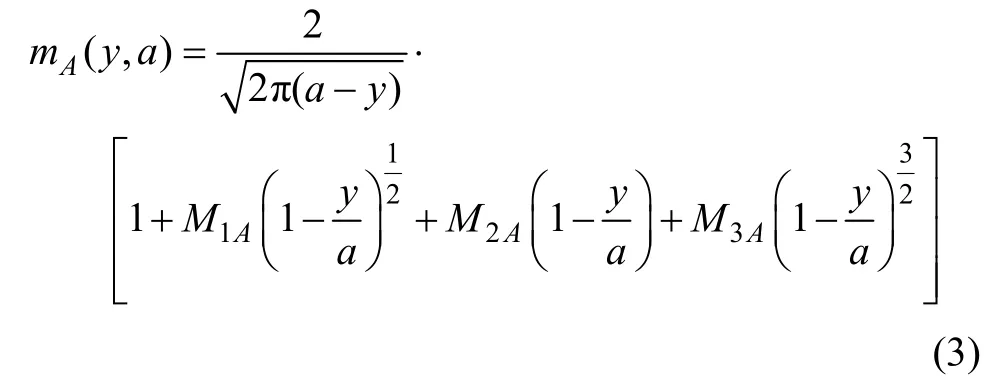
裂纹表面B点的权函数(mB(y,a))为

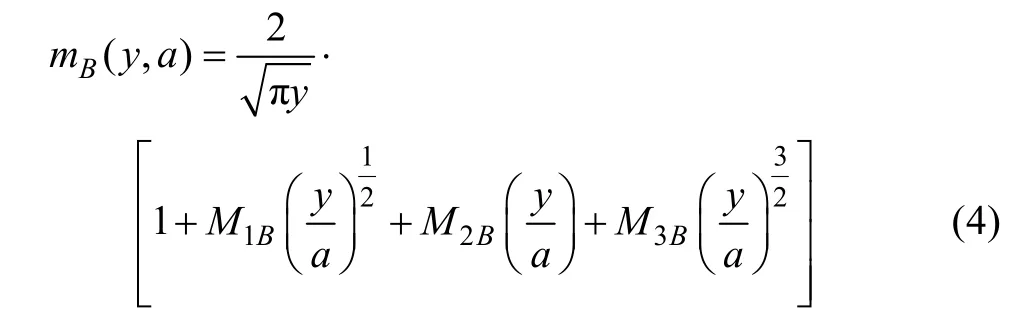
式中：MiA和MiB为权函数的系数，仅取决于裂纹的几何形状。

A、B两点的应力强度因子可以分别表示为

要得到A、B两点的应力强度因子，须先确定权函数的系数MiA和MiB。根据权函数的性质，在y=0处，有

SHIRATORI和 MIYOSHI[4]用有限元法研究半椭圆裂纹表面几种典型的应力分布，选择应力均分布和线性分布时的应力强度因子求解MiA和MiB。裂纹表面应力分布如图3所示，可表示为如下形式：

将裂纹表面应力分布函数代入式(3)和(4)中，对应的应力强度因子分别为

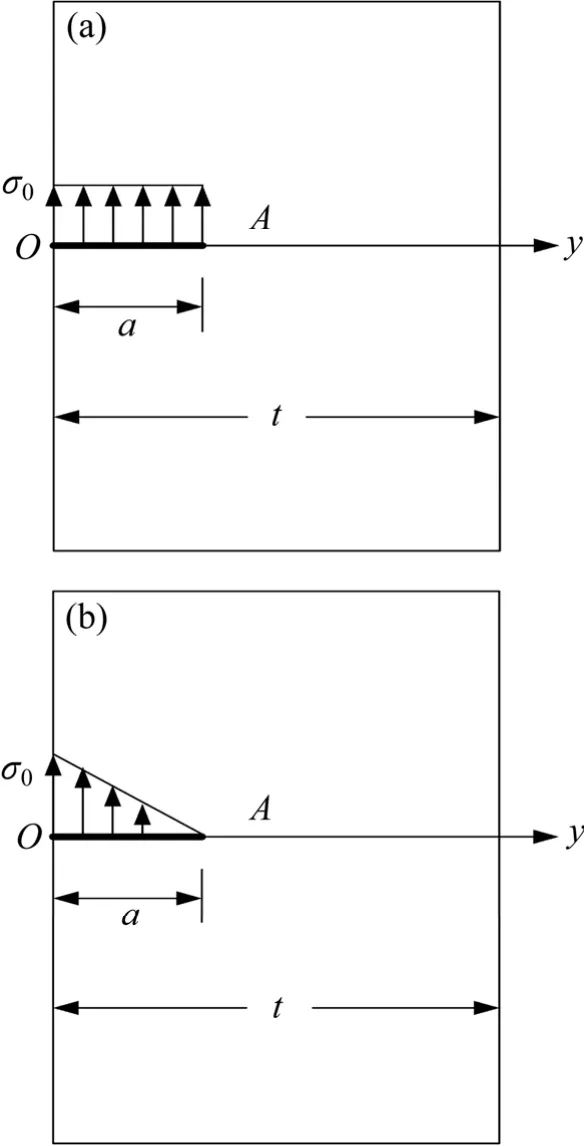
图3 裂纹表面的应力分布Fig.3 Reference stress fields of surface cracks: (a)Uniform stress field; (b)Linear stress field

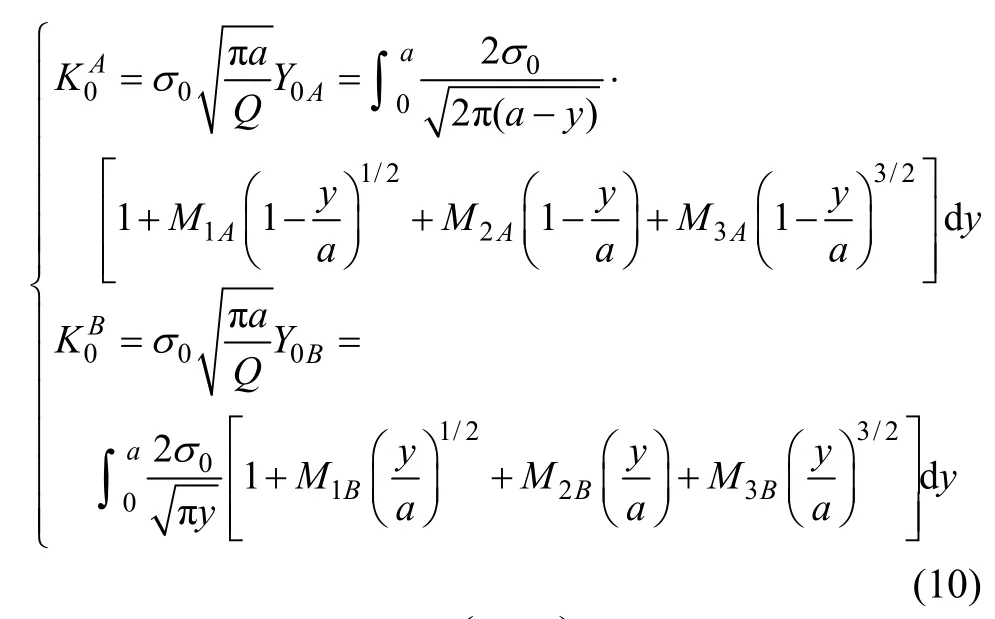
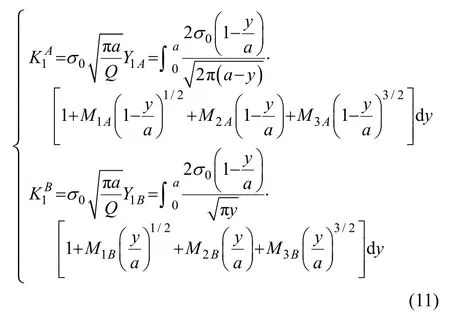
结合式(6)和(7)，可以得到A、B两点权函数系数的表达式：

根据SHIRATORI和MIYOSHI[4]的有限元计算结果，在的变化范围内，将Yi,j表示为a/t和a/c的函数：

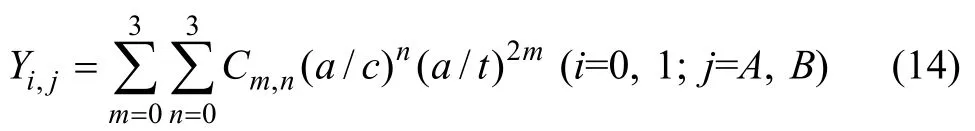
式中：Cm,n为各项系数，具体数值见表1。

解出MiA和MiB后，便确定了应力场中半椭圆裂纹A、B两点的权函数，结合式(5)便可求得A、B两点处在淬火残余应力场中的Ⅰ型应力强度因子。

3 结果与讨论

为了验证权函数的正确性，可以用文献[4]中有限元结果来检验。文献[4]中提供了几种典型的裂纹表面应力分布的数据，分别与本文权函数法计算出的结果进行对比。裂纹表面应力分布为

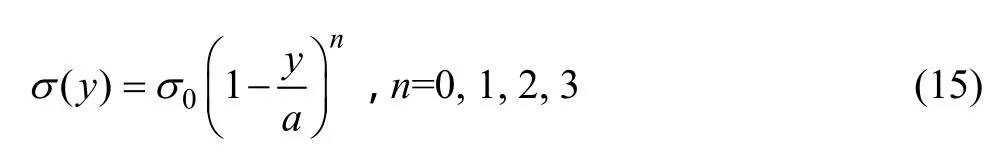
将应力强度因子无量纲化：

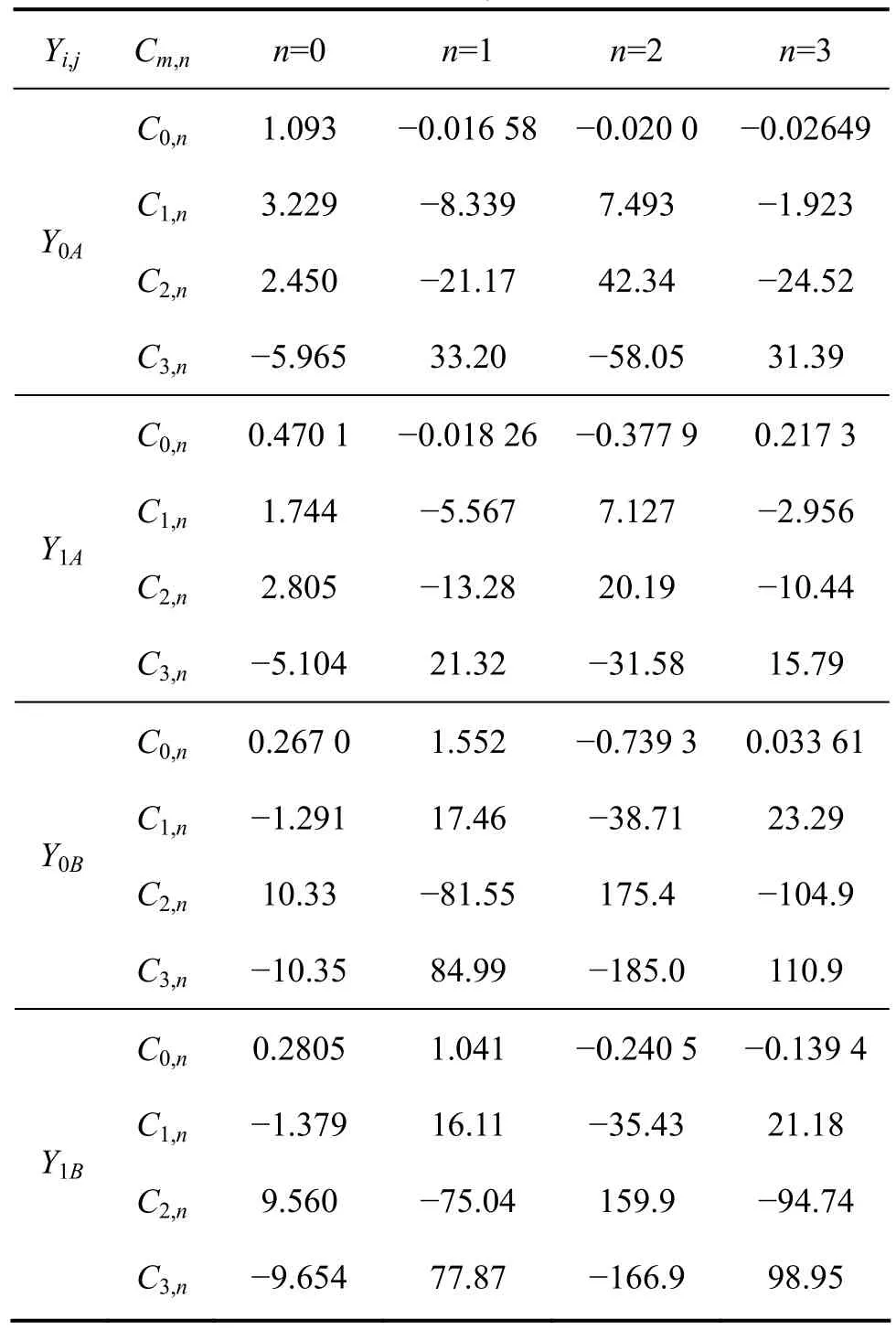
表1 Yi,j的各项拟合系数Table 1 Fitting coefficients of Yi,j

A、B两点无量纲应力强度因子的计算结果对比图分别见图4和 5，图中

从图4和5中可以看出，在4种裂纹表面应力分布的情况下，权函数法所得结果与Shiratori的有限元结果吻合良好，最大误差不超过 4%，证明所建立的权函数计算裂纹表面不同应力分布的应力强度因子精度比较高。图6所示为铝合金板A、B两点处Ⅰ型残余应力强度因子的计算结果，其中

从结果中可以看出，A点无量纲应力强度因子随着椭圆裂纹短半轴与长半轴的比值a/c增大而减小，而B点处的变化规律却相反。当裂纹短半轴与长半轴的比值a/c增大时，A点的无量纲应力强度因子先增大后减小，而B点的基本保持增大的趋势，这是因为随着裂纹的扩展，A点裂纹表面的残余应力会进入淬火残余应力的压应力区域，而B点始终位于淬火残余应力的拉应力区域。

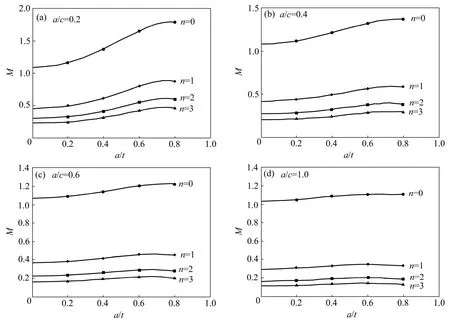
图4 A点应力强度因子计算结果与有限元数据的对比Fig.4 Comparison of weight function based stress intensity factors for point A with finite element data

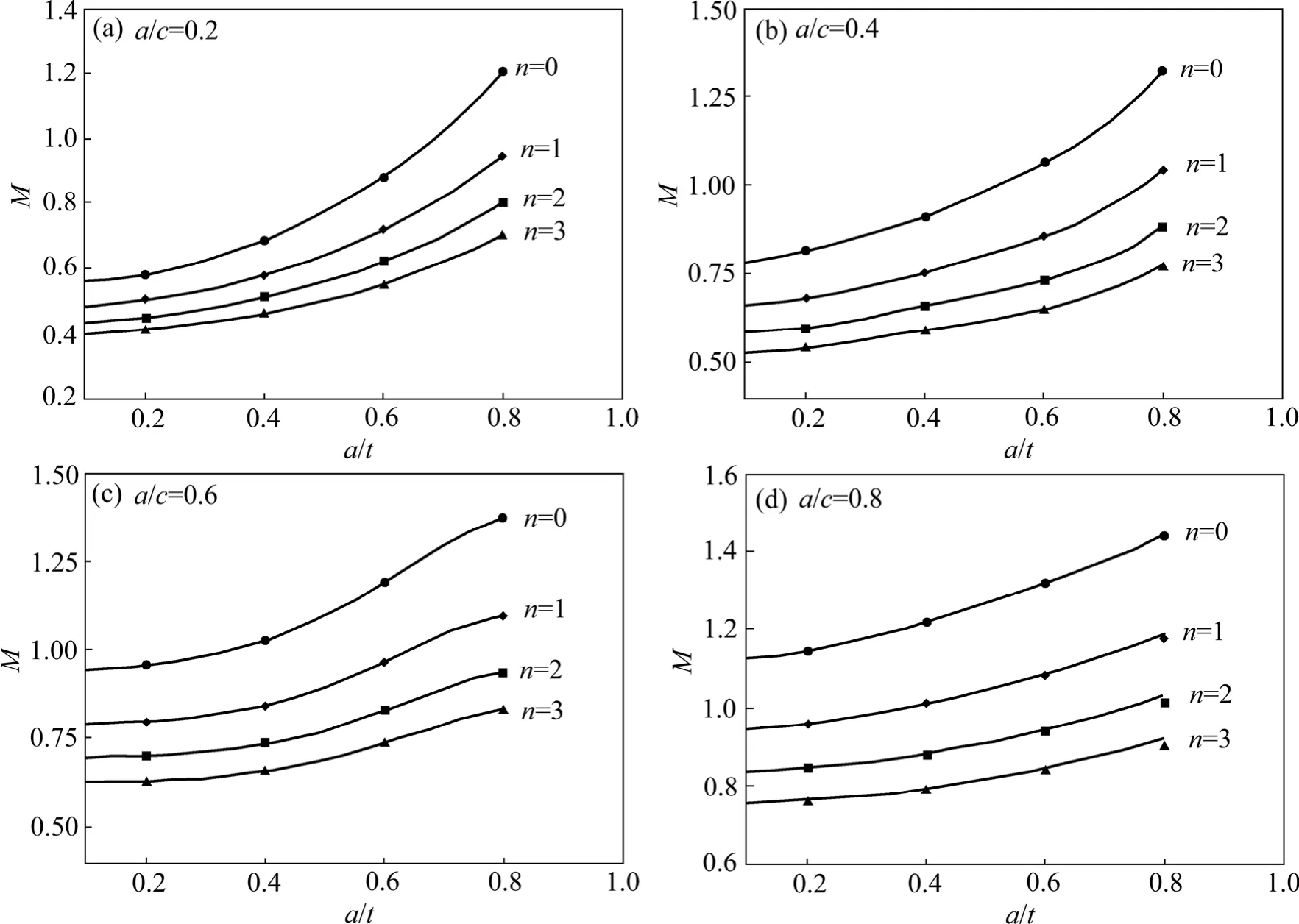
图5 B点应力强度因子计算结果与有限元数据的对比Fig.5 Comparison of weight function based stress intensity factors for point B with finite element data

图6 A点和B点处的应力强度因子Fig.6 Stress intensity factors of points A(a)and B(b)

4 结论

1)利用裂纹表面均分布和线性分布应力对应的应力强度因子确定了铝合金板椭圆裂纹Ⅰ型应力强度因子的权函数，计算了裂纹表面应力为均匀分布、线性分布、平方分布和立方分布时的应力强度因子。

2)通过实验数据和Shiratori的有限元模拟结果，将铝合金板淬火残余应力分布拟合成函数表达式，结合所确定的权函数，计算铝合金板的裂纹在淬火残余应力场中的Ⅰ型应力强度因子，结果表明，由于有淬火残余应力的影响，裂纹A点的无量纲应力强度因子随裂纹的扩展而增大的趋势与裂纹B点的趋势并不一样。

3)所建立的权函数方法不仅能有效地计算裂纹在淬火残余应力场中的应力强度因子，同时也适用于焊接应力、热应力等复杂应力场中裂纹应力强度因子的计算。

[1]柯映林, 董辉跃.7075铝合金厚板预拉伸模拟分析及其在淬火残余应力消除中的应用[J].中国有色金属学报, 2004, 14(4):639-645.KE Ying-lin, DONG Hui-yue.Pre-stretching process and its application in reducing residual stress of quenched 7075 aluminum alloy thick plates[J].The Chinese Journal of Nonferrous Metals, 2004, 14(4): 639-645.

[2]朱才朝, 罗家元, 李大峰, 钟 渝, 李 云.基于流变应力特性的铝合金淬火残余应力数值模拟及试验研究[J].机械工程学报, 2010, 46(22): 41-46.ZHU Cai-chao, LUO Jia-yuan, LI Da-feng, ZHONG Yu, LI Yun.Numerical simulation and experimental investigation of the aluminum alloy quenching-induced residual stress by considering the flow stress characteristic[J].Journal of Mechanical Engineering, 2010, 46(22): 41-46.

[3]NEWMAN J C, RAIU I S.An empirical stress intensity factor equation for the surface crack[J].Eng Fract Mech, 1981, 15:185-192.

[4]SHIRATORI M, MIYOSHI T.Weighting function for a semi-elliptical surface crack in a plate under basic mode of stress distribution[M].Oxford: Pergamon Press, 1992: 725-730.

[5]BUCKNER H F.A novel principle for the computation of stress intensity factors[J].Zeitschrift fur Angewandte Mathematik und Mechanik, 1970, 50: 529-546.

[6]RICE J R.Some remarks on elastic crack-tip stress field[J].International Journal of Solids and Structures, 1972, 8: 751-758.

[7]PETROSKI H J.ACHENBACH I D.Computation of the weight function from a stress intensity factor[J].Eng Fract Mech, 1978,10: 257-266.

[8]VAINSHTOK V A, VARFOLOMEYEV I V.Stress intensity factor analysis for part-elliptical cracks in structures[J].Int J Fract, 1990, 46: 1-24.

[9]WU S R, CLARSSON A J.Weight functions and stress intensity factor solutions[M].Oxford: Pergamon Press, 1991.

[10]GLINKA G, SHEN G.Universal features of weight functions for cracks in mode Ⅰ[J].Eng Fract Mech, 1991, 40: 1135-1146.

[11]SHEN G, GLINKA G.Weight functions for a surface semi-elliptical crack in a finite thickness plate[J].Theoretical and Applied Fracture Mechanics, 1991, 15: 247-255.

[12]ZHENG X J, GLINKA G, DUBEY R N.Stress intensity factors and weight functions for a corner crack in a finite thickness plate[J].Eng Fract Mech, 1996, 51: 49-61.

[13]LAMMI C J, LADOS D A.Effects of residual stresses on fatigue crack growth behavior of structural materials: Analytical corrections[J].International Journal of Fatigue, 2011, 33:858-867.

[14]BAO R, ZHANG X, YAHAYA N A.Evaluating stress intensity factors due to weld residual stresses by the weight function and finite element methods[J].Engineering Fracture Mechanics,2010, 77: 2550-2566.

[15]张园园, 吴运新, 李丽敏, 张明容.7075铝合金预拉伸板淬火后残余应力的有限元模拟[J].材料热处理技术, 2008, 37(14):88-91.ZHANG Yuan-yuan, WU Yun-xin, LI Li-min, ZHANG Ming-rong.Finite element simulation of residual stress in pre-stretching thick-plates of 7075 aluminum alloy after quenching[J].Material & Heat Treatment, 2008, 37(14): 88-91.

[16]林高用, 郑小燕, 冯 迪, 杨 伟, 彭大暑.铝合金厚板淬火残余应力的研究进展[J].材料导报, 2008, 22(6): 70-74.LIN Gao-yong, ZHENG Xiao-yan, FENG Di, YANG Wei,PENG Da-shu.Research development of quenching-induced residual stress of aluminum thick plates[J].Materials Review,2008, 22(6): 70-74.

[17]WANG X, LAMBERT S B.Stress intensity factors for low aspect ratio semi-elliptical surface cracks infinite thickness plates subjected to nonuniform stresses[J].Eng Fract Mech, 1995,51: 517-532.

[18]WANG X, LAMBERT S B.Stress intensity factors and weight functions for high aspect ratio semi-elliptical surface cracks infinite-thickness plates[J].Eng Fract Mech, 1997, 57: 13-21.