数值求解一类空间分数阶扩散方程源项系数反问题

阮周生，张文，王泽文

（1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，江西 抚州 344000；2.东华理工大学 理学院，江西 南昌 330013）

数值求解一类空间分数阶扩散方程源项系数反问题

阮周生1，2，张文1，2，王泽文2

（1.东华理工大学 放射性地质与勘探技术国防重点学科实验室，江西 抚州 344000；2.东华理工大学 理学院，江西 南昌 330013）

数值求解一类空间分数阶扩散方程源项系数反问题.利用函数变换，将源项系数反问题转为对应的定解问题，利用隐式差分格式，求解对应定解问题，然后利用数值积分，求得待定系数函数的数值解，并且证明了隐式差分格式的绝对稳定性.通过数值算例表明，该数值方法具有较高的计算精度.

反常扩散；空间分数阶导数；反问题；有限差分格式；稳定性

MSC 2010：35K05

反常扩散现象在自然界广泛存在，反常扩散过程本质上是时间上有记忆性和空间非局域性的过程，故利用整数阶扩散方程不能准确地描述这类反常扩散过程，分数阶扩散方程在描述自然界反常扩散现象中起着非常重要的作用，其基本思想是利用对时间（或空间）的分数阶导数代替整数阶时间（或空间）导数，从而能够较精确地描述有记忆和遗传、路径依赖性质的物理过程，在半导体、核磁共振、多孔介质、高分子聚合物、湍流、固体表面扩散、胶体中的输运、量子光学、分子光谱、经济金融都有广泛的应用［1-6］.常福宣等利用分数阶对流-弥散方程的Lévy分布解来模拟空间点溶质浓度的时间变化过程比用传统的二阶对流-弥散方程所得的高斯分布解来模拟效果更好［2］；孙洪广等对空间分数阶导数“反常”扩散方程的3种数值算法进行比较［3］；王晟等将Fick扩散定律的Fourier三角级数算法推广成多孔材料分形扩散模型的Fourier-Bessel级数算法，并把它应用于化学工程中吸附问题涉及的浓度分布与相对吸附量的计算中，取得一些规律性认识［4］.

近年来，分数阶对流扩散方程反问题越来越引起国内外学者的关注，谷文娟［5］等利用最佳摄动量法研究了一维时间分数阶扩散方程中同时确定分数微分阶数与扩散系数的数值反演问题.Battaglis［7］等求解了分数阶热传导反问题.Murio［8］建立了一类分数阶扩散方程反问题的稳定数值方法；Murio［9］分析了Caputo's时间分数阶热传导问题.Sivaprasad［10］等利用反灵敏分析研究了分数阶动力衰减系统.Cresson［11］讨论了分数阶微分方程反问题，并得到了一些微分方程的拉格朗日结构，最近魏慧利用最佳摄动量方法数值求解了一类分数阶抛物型方程扩散系数反问题［12］.

本文考虑下面系数反问题，即找｛p（t），u（x，t）｝，使得满足问题

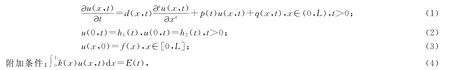
其中扩散系数d（x，t），源项q（x，t），边界条件函数h1（t），h2（t），初始条件函数f（x）为已知函数，k（x）表示求解区间［0，L］内1已知函数，E（t）为测量数据，p（t）为未知系数函数.问题（1）～（4）可视为源项控制反问题，通过在求解区域内源项产生能量的变化规律来反演源项系数p（t）.

程系数p（t）反问题已经有许多学者研究过，见文献［13-17］.

1 问题转换

2 隐式差分格式的建立

在时间方向上采用一阶向前差商，离散上述反常扩散方程中的一阶时间偏导数，有在空间上使用修正的向前Grünwald-Letnikov定义来表示空间α阶导数［3］，

3 系数函数p（t）数值求解

4 数值等例

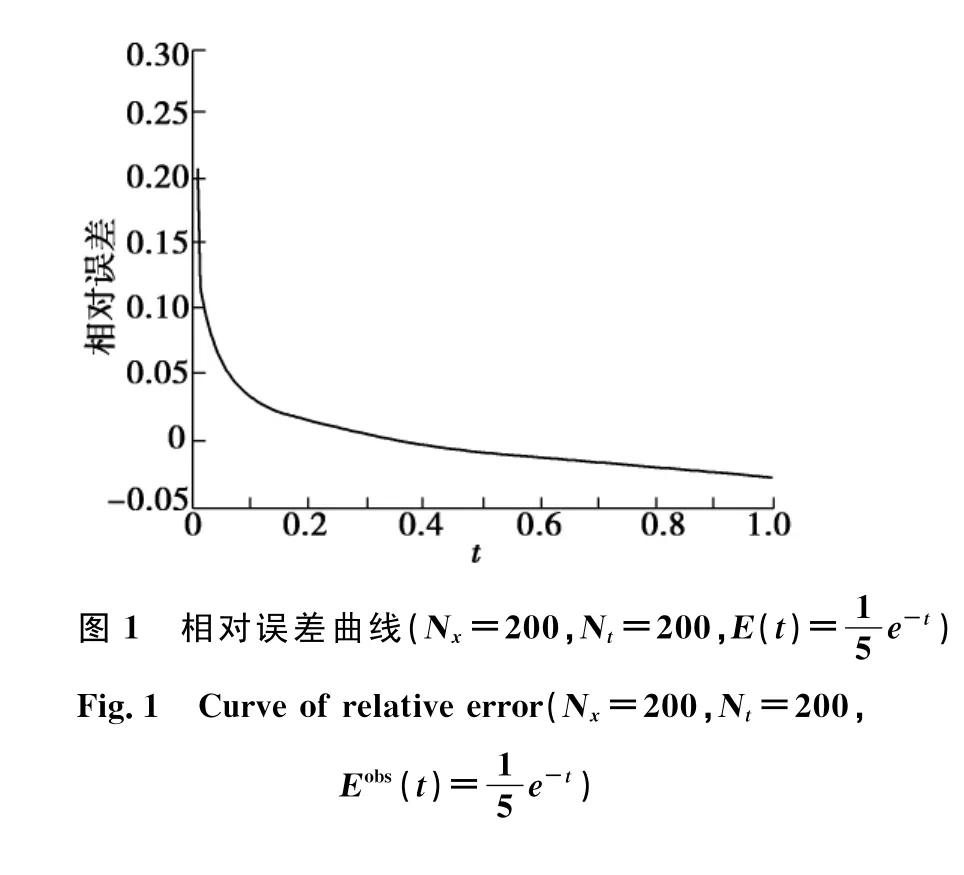
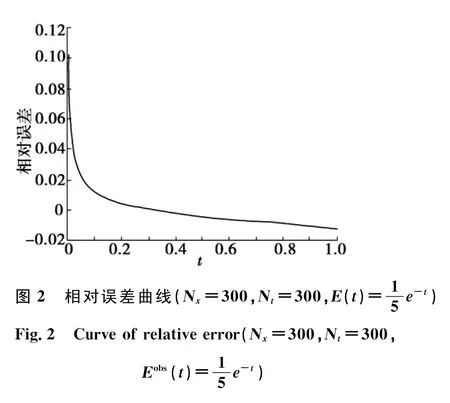
5 结论

研究了一类一维分数阶扩散方程源项系数反问题的数值计算方法，证明了差分格式的无条件稳定性.从数值模拟来看，当Nx与Nt的取值越大时，精度越高.本文的数值方法同样可以应用到二维分数阶扩散方程源项系数反问题.

［1］ PODLUBNY I.Fractional differential equation［M］.San Diego：Academic Press，1999：50-78.

［2］ 常福宣，吴吉春，戴水汉.多孔介质溶质运移的分数弥散过程与Lévy分布［J］.南京大学学报：自然科学版，2004，40（3）：287-291.

CHANG Fuxuan，WU Jichun，DAI Shuihan.The fractional dispersion in pore medium and lévy distribution［J］.Journal of Nanjing University：Natural Sciences，2004，40（3）：287-291.

［3］ 孙洪广，陈文，蔡行.空间分数阶导数“反常”扩散方程数值算法的比较［J］.计算物理，2009，26（5）：719-724.

SUN Hongguang，CHEN Wen，CAI Hang.Comparative study of numerical algorithms for‘anomalous’diffusion equation with spatial fractional derivatives［J］.Chinese Journal of Computational Physics，2009，26（5）：719-724.

［4］ 王晟，马正飞，姚虎卿.多孔材料分形扩散模型的Fourier-Bessel级数算法及其应用［J］.计算物理，2008，25（3）：289-295.

WANG Sheng，MA Zhengfei，YAO Huqing.Fourier-bessel series algorithm in fractal diffusion model for porous material［J］.Chinese Journal of Computational Physics，2008，25（3）：289-295.

［5］ 谷文娟，李功胜，殷凤兰，等.一个时间分数阶扩散方程的参数反演问题［J］.山东理工大学学报：自然科学版，2010，24（6）：22-25.

GU Wenjuan，LI Gongsheng，YIN Fenglan.Parameters inversion for a time fractional diffusion equation［J］.Journal of Shandong Unirersity of Technology：Natural Science Edition，2010，24（6）：22-25.

［6］ 王济平.一维热传导方程不适定问题的解法［J］.河北大学学报：自然科学版，1988，8（3）：6-11.

Wang Jiping.The solution of an ill-posed problem for one-dimension heat transport equation［J］.Journal of Hebei University：Natural Science Edition，1988，8（3）：6-11.

［7］ BATAGLIA J L，COIS O，PUIGSEGUR L，et al.Solving an inverse heat conduction problem using a non-integer identified model［J］.International Journal of Heat and Mass Transfer，2001，44：2671-2680.

［8］ MURIO D A.Stable numerical solution of a fractional-diffusion inverse heat conduction problem［J］.Computers ＆Mathematics with Applications，2007，3：1492-1501.

［9］ MURIO D A.Time fractional IHCP with Caputo fractional derivatives［J］.Computers ＆ Mathematics with Applica-tions，2008，56：2371-2381.

［10］ SIVAPRASAD R，VENKATESHA S，MANOHAR C S.Identification of dynamical systems with fractional derivative damping models using inverse sensitivity analysis［J］.CMC，2009，298：1-29.

［11］ CRESSON J.Inverse problem of fractional calculus of variations for partial differential equations［J］.Communications in Nonlinear Science and Numerical Simulation，2010，15：987-996.

［12］ WEI Hui，CHEN Wen，SUN Hongguang，et al.A coupled method for inverse source problem of spatial fractional anomalous diffusion equations［J］.Inverse Problems in Science and Engineering，2010，18：945-956.

［13］ CANNON J R，LIN Y，XU S.Numerical procedures for the determination of an unknown coefficient in semi-linear parabolic differential equations［J］.Inverse Probl，1994，10：227-243.

［14］ MEHDI D.Finding a control parameter in one-dimensional parabolic equation［J］.Applied Mathematics and Computation，2003，135：491-503.

［15］ MEHDI D.Determination of a control function in three-dimensional parabolic equations［J］.Mathematics and Computers in Simulation，2003，61：89-100.

［16］ MEHDI D.Finite difference schemes for two-dimensional parabolic inverse problem with temperature overspecification［J］.International Journal of Computer Mathematics，2000，75：339-349.

［17］ MEHDI D，MEHDI T.Determination of a control parameter in a one-dimensional parabolic equation using the method of radial basis functions［J］.Mathematical and Computer Modeling，2006，44：1160-1168.

Numerical solution of source terms coefficient inverse problem for a kind of space fractional diffusion equation

RUAN Zhousheng1，2，ZHANG Wen1，2，WANG Zewen2
（1.Key Laboratory of Radioactive Geology and Exploration Technology Fundamental Science for National Defense，East China Institute of Technology，Fuzhou 344000，China；2.College of Science，East China Institute of Technology，Nanchang 330013，China）

A numerical method for source coefficient inverse problem of a kind of one-dimensional space fractional diffusion equation is concerned.The inverse problem of source coefficient is converted to the corresponding definite problem through function transformation.Applying the implicit difference，the solution of the corresponding definite problem is founded.Using the numerical integral，the numerical solution of the undetermined function is founded，and the unconditional stability of difference scheme is proved.The numerical example shows that the proposed method has high accuracy.

anomalous diffusion；spatial fractional derivative；inverse problem；finite difference scheme；stability

O175

A

1000-1565（2012）05-0458-06

2011-10-11

国家自然科学基金资助项目（41001320，11161002）；江西省自然科学基金资助项目（2009GZS0001）；江西省教育厅科技资助项目（GJJ11151）；放射性地质与勘探技术国防重点学科实验室资助项目（2010RGET12）

阮周生（1980-），男，江西吉安人，东华理工大学讲师，主要从事偏微分方程正反问题的算法与理论研究.

E-mail：zhshruan＠ecit.cn

王兰英）