导电加热切削有限元仿真及试验研究
刘 新 徐文骥 孙 晶 张 琳
大连理工大学,大连,116024
0 引言
导电加热切削(electric hot machining,EHM)是一种利用刀具和工件构成回路,通以低压大电流使局部切削区材料软化,从而提高材料切削加工性能的绿色切削技术[1]。
EHM 延长刀具寿命和提高已加工表面质量的关键是通过调整加热电流,使切削过程工作在最佳切削温度区间内[2-3]。赵学智等[4-5]针对Kainth模型[6]的缺陷,提出了改进的加热电阻模型和经验公式。EHM是一个热、力、电不断耦合的复杂过程,对EHM进行建模和有限元仿真有助于建立适合EHM的加工参数数据库,有助于分析切削用量和电参数对EHM过程的影响。但当前对EHM进行三维建模和有限元仿真的工作才刚刚起步。
近年来,用有限元法对金属切削过程进行仿真发展迅速,但针对EHM的有限元仿真仅有基于非稳态热传导方法建立的EHM钻削温度的有限元模型[7]。采用该模型进行有限元仿真时,将一特定的温度作为整个工件初始温度,忽略了加热电流变化对焦耳热产生温升的影响,因此其热量的加载方式不尽合理。另外,对车削中应用EHM有限元仿真的研究未见报道。有必要针对车削中EHM加热电阻热加载方式和三维有限元模型进行深入研究,实现对EHM热力耦合场较为准确的有限元仿真。
本文在分析EHM基本原理的基础上,通过正交回归试验建立EHM加热电阻经验公式;利用加热电阻经验公式,将加热电阻焦耳热作用于切削区进行有限元分析,归纳出EHM使切削区产生温升的经验公式;利用三维切削模型和本构方程,对EHM切削过程的热-力耦合场进行有限元仿真与试验验证。
1 EHM基本原理
EHM的实质是对切削区温度进行正补偿,以提高工件材料的切削加工性能。当金属切削过程在适当的切削区温度下进行时,可以使刀具和工件材料保持较大的硬度差,减少刀具磨损,延长刀具寿命,同时抑制积屑瘤和鳞刺,提高已加工表面质量。
EHM基本原理如图1所示。电源正极与工件相连,电源负极与刀具相连,在工件与刀具之间通以加热电流。当电流流经切削变形区和刀具尖端时,切削区工件材料在切削热和加热电阻焦耳热的共同作用下发生加热软化效应,从而使切削变得顺利。
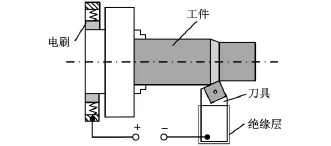
图1 EHM原理图
2 加热电阻
对EHM的热-力耦合场进行有限元仿真,首先需确定EHM切削区热量的来源及大小。除切削生热外,加热电阻的焦耳热是切削区热量的主要来源。
2.1 加热电阻三维模型
EHM加热电阻主要由金属材料电阻、接触电阻和收缩电阻组成。EHM过程中切削区加热电阻的三维模型如图2所示。AA'O'O为剪切面,OO'D'D所在表面为前刀面,OO'C'C所在表面为后刀面,箭线表示电流流经的路径。图2中,切屑的变形区AA'B'BOO'和刀尖多面体OO'D'DCC'的材料电阻构成金属材料电阻;刀屑接触面OO'B'B和刀工接触面OO'C'C上的电阻构成接触电阻;电流由工件流向刀具时,导电面积急剧变小,电流线密度发生收缩,形成收缩电阻[8]。
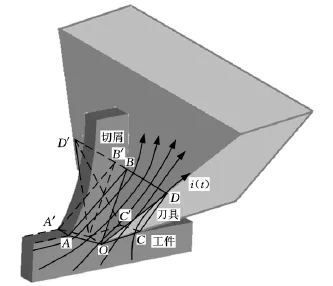
图2 EHM加热电阻三维模型
2.2 加热电阻经验公式
研究各加工参数对加热电阻的影响,建立加热电阻的经验公式,是对EHM热-力耦合场进行建模和有限元仿真的前提条件。采用图3所示的试验装置,通过机床主轴尾部的集流环采集刀具和工件之间的电压降,用伏安法测量加热电阻。
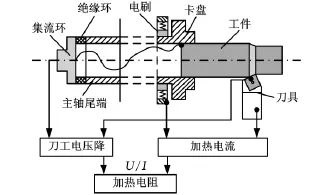
图3 EHM加热电阻检测装置示意图
试验在普通车床上进行,工件的材质为GCr15(52100),外径为87mm,硬度为 HRC60;刀具采用机夹可转位车刀,牌号为YT726,刀片型号为41605H;刀杆主偏角 κr=75°,前角 γ0=20°,后角α0=-8°。采用L16(45)正交表进行检测加热电阻的正交试验,试验数据见表1。
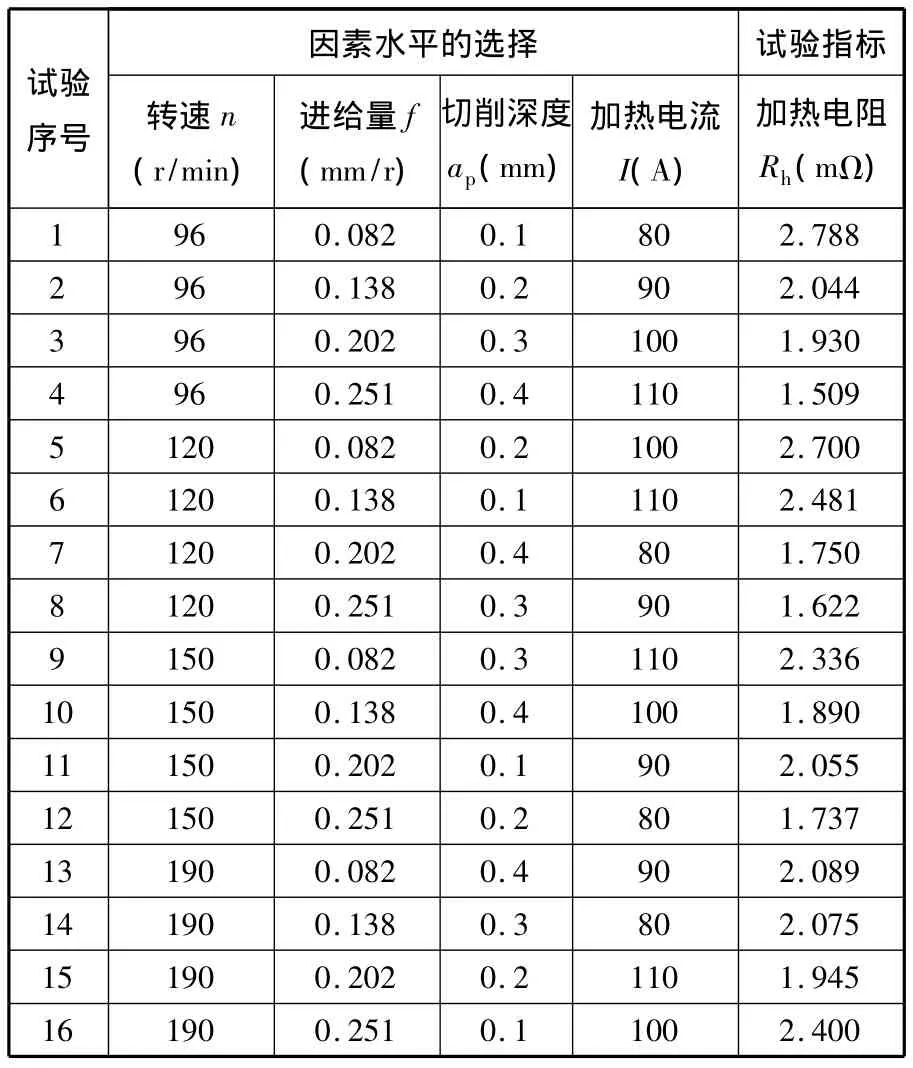
表1 检测加热电阻的正交试验数据
对表1中数据进行多元线性回归,得到EHM加热电阻经验公式:
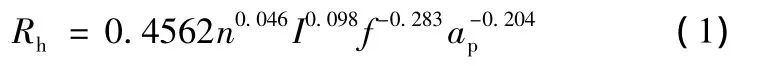
由式(1)可得,EHM的加热电阻随着进给量、切削深度的增大而减小,随着切削速度、加热电流的增加而增大;其中,加热电流对加热电阻的影响最大,进给量的影响最小,切削速度和切削深度对加热电阻的影响相近。加热电流通过加热电阻的焦耳热直接影响切削区温度场的分布,一方面温度和电场分布的变化会改变刀具-工件、刀具-切屑接触面的接触状态,影响接触电阻;另一方面切削温度的变化直接通过金属材料电阻率的变化影响加热电阻,因此加热电流对加热电阻的变化影响最大。
利用各因素和误差的变动平方和S以及自由度U求出平均变动平方和S/U,则F比的值为各因素和误差平均变动平方和之比。给出显著度α=0.05,将各因素的F比和F检验的临界值进行对比,即可判断某因素的显著性。对表1的正交试验数据进行方差分析,结果如表2所示。
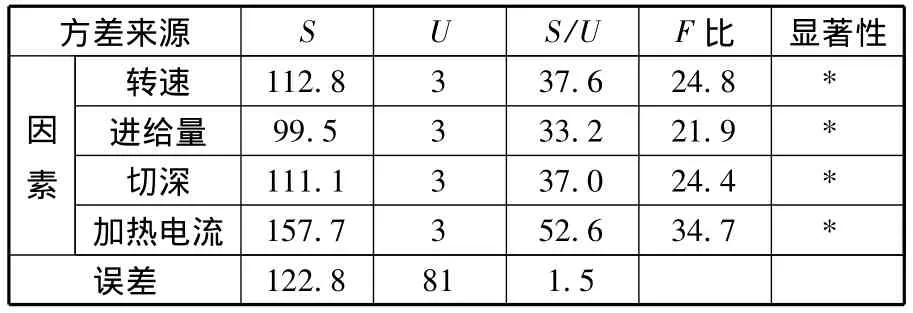
表2 EHM加热电阻正交试验方差分析结果
表2的方差分析结果表明,多元线性回归的效果是显著的,式(1)可较为准确地表示加热电阻与各因素之间的变化关系,可以应用此经验公式对EHM加热电阻进行分析与计算。其他刀具和工件材料的组合也可以用此类正交回归试验的方法获取EHM加热电阻经验公式。
3 EHM三维有限元仿真
EHM过程中,加热电流对局部切削区材料进行快速加热时,加热电阻生成的焦尔热与塑性变形生热、摩擦热等共同影响着切削区的温度场分布;温度通过材料的本构方程影响着切削区的应力分布;与此同时,刀具和工件的相对运动会引起局部切削区应力分布和接触面摩擦状态的改变,从而影响塑性变形热、摩擦热和电接触状态。因此,EHM是一个电、力、热相互耦合的复杂过程。对EHM进行有限元仿真将有助于分析切削用量和电参数对EHM的影响,有助于建立适合EHM的加工参数数据库。
EHM切削区温升是加热电阻焦耳热所产生的温升与切削本身所产生的温升叠加的结果。因此,本文将EHM过程看作是导电加热和切削两个过程的叠加,将加热电阻焦耳热所引起的切削区温升作为工件材料的初始温升。
本文有限元仿真的条件:室温为25℃,工件材料为GCr15(AISI52100),刀具材料为YT726,刀具几何角度 γ0=20 °,α0= -8 °。
3.1 工件材料的初始温度
EHM加热电阻产生的切削区温升由加热电阻的焦耳热产生。使用ANSYS单元PLANE55和图2所示的加热电阻三维模型,借助式(1)对EHM中加热电流引起的切削区材料温度场变化进行有限元分析。
为简化问题,作出如下假设:
(1)金属切削时消耗的能量除转化为热能外,有1%~2%的能量以形成新表面和晶格扭曲等形式形成潜能[9]。由于此能量相对较小且很难估算,故假设切削耗能全部转换为热量。
(2)干式切削时,切削区向周围介质直接传出的热量不到切削产热总能量的1%[10],忽略不计。
(3)加热电阻生成的热量载荷全部均匀作用于图2中切削变形区材料AA'B'BOO'和刀尖材料CC'D'DOO'处,以热传导的形式加热切屑、工件以及刀具,待热平衡后,将此时的切削区温升作为因加热电流产生的切削区材料的平均温升。
经有限元分析可知,焦耳热引起的切削区材料的平均温升随加热电流的变化如图4所示。加热电流小于100A时,加热效果并不显著;加热电流大于100A时,切削区材料的平均温升随着加热电流的增大而迅速增大。将切削区材料的平均温升视为工件材料的初始温升,对图4的数据进行最小二乘法拟合,得到工件材料初始温度θp(℃)的经验公式:
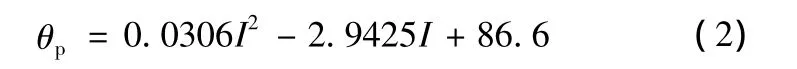
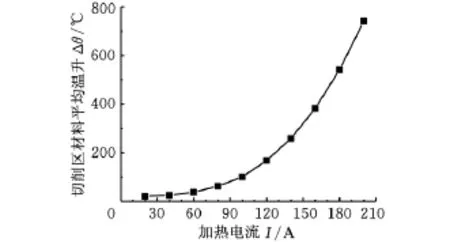
图4 加热电流对切削区材料平均温升的影响
3.2 三维切削有限元模型
采用有限元软件DEFORM-3D对EHM切削过程进行三维有限元仿真。建立切削模型时,材料的本构方程和刀具角度是最重要的输入参数。刀具的几何模型使用三维绘图软件绘制,将其转成STL格式后导入DEFORM-3D。
假设切削过程中,工件和刀具之间的相对运动状态不随时间变化。把工件外表面切削层展开,根据有限元离散的思想,把工件看成是许多平板的叠加。从主运动方向来看,在平行于基面的平面上,被切削材料就是一个矩形平板。
划分网格时,将工件划分为70 000个实体单元。为得到较高的仿真精度,将网格中剪切变形区附近的实体单元划分得较为密集。最后,在工件下表面施加全约束,将工件的旋转运动转化为刀具沿着主运动方向的直线运动。同时,把进给速度施加在进给运动方向上。三维正交切削有限元模型如图5所示。
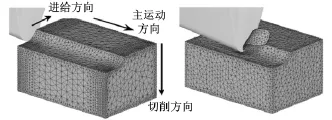
图5 三维切削模型示意图
3.3 工件材料本构方程
材料的本构方程是用来描述等效应力与应变、应变率、温度之间的关系的。选择合理的工件材料本构方程是保证有限元仿真准确性的基础。
EHM主要靠加热电流软化切削区材料,降低其强度和硬度。当硬度改变后,材料的流动应力会随之改变。因此,本文选择了与硬度相关的Umbrello 本构方程[11]:
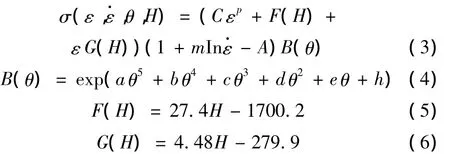
式中,σ为流动应力;ε为等效应变;ε·为等效应变率;H为工件的洛氏硬度;θ为工件温度,℃;C、p、A、m、a、b、c、d、e、h为流动应力模型参数,C=1092,p=0.083,A=0.0567,m=0.1259,a=3.8121 × 10-15,b= - 3.2927 × 10-12,c= - 6.9118 × 10-9,d=5.4993 × 10-6,e= - 1.2419 ×10-3,h=0.024 43。
3.4 切削力有限元仿真
利用式(2)计算出工件材料的初始温度,采用Umbrello本构方程(式(3)~式(6)),通过图5所示的三维直角正交切削有限元模型,对EHM过程的切削力和温度场分布进行有限元仿真。
加热电流对主切削力产生的影响如图6所示。随着加热电流的增大,主切削力逐渐减小:I<80A时,主切削力下降较为平缓;80A≤I<160A时,主切削力下降较快;I≥160A后,主切削力的变化不大,此时EHM的主切削力已较不加入电流时下降了约30%。在图6的切削用量下,加热电流I≥160A可以得到较小的切削力。同理,对EHM的三维有限元仿真可以得到不同加工条件下的切削力,获取具有较小切削力的加工参数。
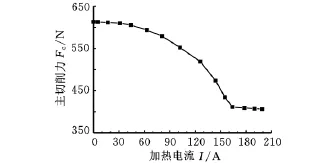
图6 加热电流对主切削力的影响
3.5 切削区温度场有限元仿真
假设加工参数为n=150r/min,f=0.138mm/r,ap=0.4mm,I=126A,对 EHM 的切削区温度场分布进行三维有限元仿真。随着EHM切削的进行,切削区温度场的演变过程如图7所示。
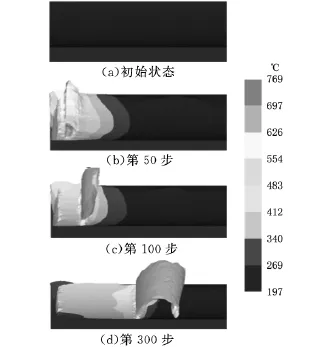
图7 EHM过程切削区温度场分布
图7a所示为工件的初始状态,由式(2)可求出,加热电流 I=126A时,工件初始温度 θp=201.6℃。切削初期如图7b所示,切削刃附近的工件材料因受挤压而产生塑性变形,切削区温度迅速升高。如图7c、图7d所示,随着切削的进行,温度场变化趋于平稳,剪切变形区温度约500℃,切屑处出现切削温度最高值,超过626℃。这是因为切屑与刀具前刀面剧烈摩擦,产生大量的摩擦热。同时,切屑与刀具前刀面接触面因摩擦形成了收缩电阻[12],通过电流后此处会迅速生成大量焦耳热。另外,EHM是干式切削,没有使用冷却介质,热量主要随切屑的流出而消耗,因此切屑处会出现切削变形区的最高温。
3.6 最佳加热电流
EHM通过对切削温度进行温度补偿改善工件材料的切削加工性能。当EHM温度补偿使切削温度处于一个最佳范围时,可以抑制积屑瘤和鳞刺,提高已加工表面质量,同时使刀-工材料间保持较大的硬度差,延长刀具寿命,使EHM处于最佳切削温度范围的加热电流称为EHM最佳加热电流。
使用硬质合金刀具进行切削时,最佳切削温度范围为600~800℃[13],使θ保持在此区间内的加热电流即最佳加热电流。
对EHM不同加热电流下前刀面接触区的平均温度θ进行有限元仿真,结果如图8所示。由图8可知,加热电流为168~190A时,前刀面接触区平均温度θ为600~800℃,即在最佳切削温度的区间内。因此,此切削用量下EHM最佳加热电流为168~190A。同理,对EHM的温度场进行三维有限元仿真,可以得到不同切削条件下的EHM最佳加热电流。
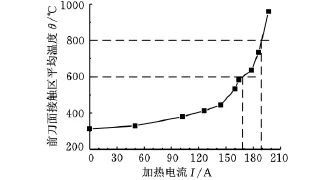
图8 加热电流I对前刀面接触区平均温度θ的影响
4 有限元仿真试验验证
金属切削有限元模型对实际切削过程做了一定的简化和假设,与实际切削情况存在差异,需要验证该模型的准确程度。切削力是反映切削状态的一个重要指标,方便测量且可重复性强。下面将对EHM的切削力进行测量,通过对比EHM切削力的有限元仿真值和试验值的差异,验证本文所建立EHM三维有限元模型的可靠性。
验证试验的切削与加热装置与图3中相同。切削力测试仪器为YDCB-Ⅲ05压电式测力仪。试验中使用云母片作为绝缘介质,将刀具与测力仪、测力仪和车床进行电气隔离,以保证测力仪的电荷信号不受干扰。采用L16(45)正交试验,因素及水平值的选取如表3所示,分析EHM切削力的有限元仿真值与实测值之间的差异。对比结果如图9所示。
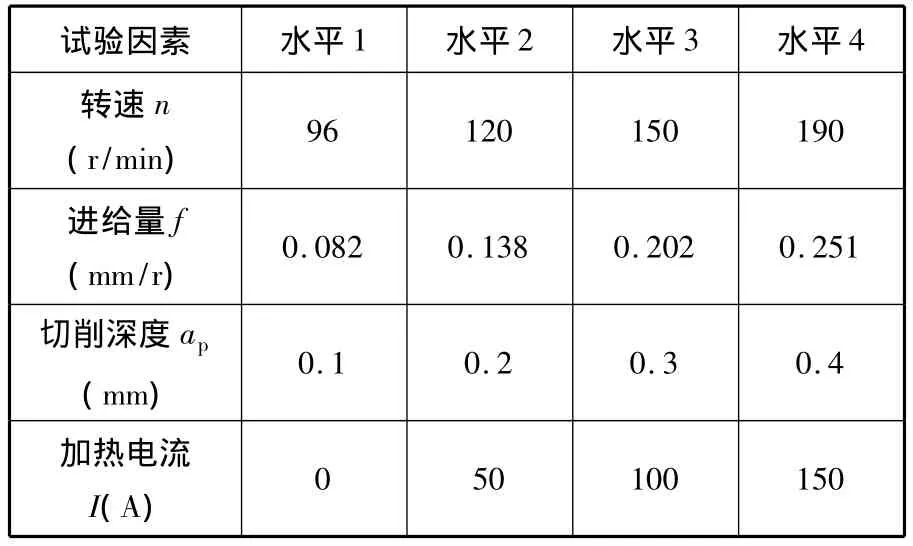
表3 验证试验正交试验表
如图9所示,在试验选取的切削用量下,EHM切削力有限元模拟的结果与验证试验的结果基本符合,具有相同的变化趋势。因此,可以认为本文所建立的EHM三维有限元模型基本符合EHM切削加工中热-力耦合场的实际情况,EHM有限元仿真的结果具有一定的可信度。
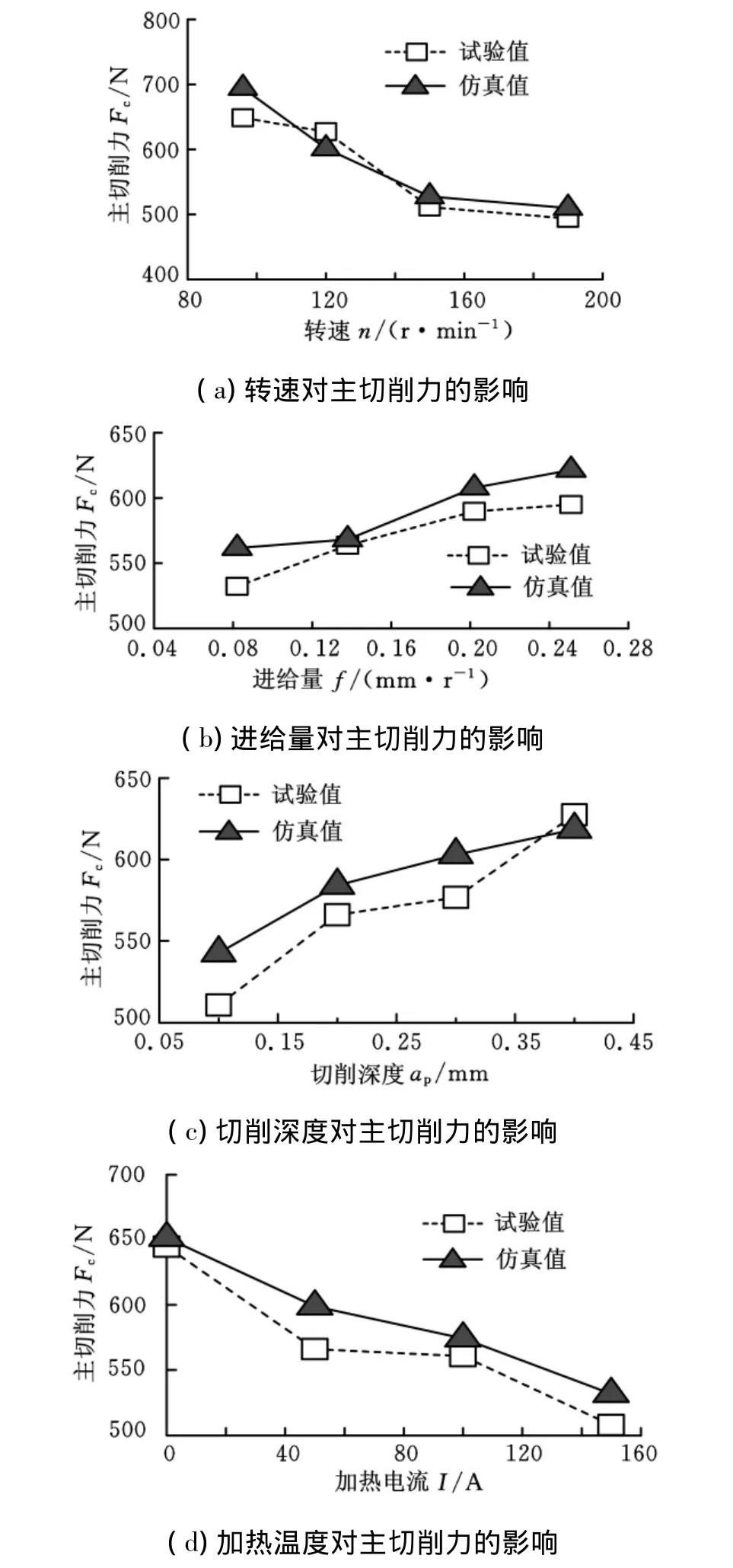
图9 主切削力的有限元模拟结果与试验结果对比
5 结论
(1)通过正交回归试验得到的加热电阻经验公式表明,EHM的加热电阻随着转速、加热电流的增大而增大,随着进给量、切削深度的增大而减小,其中,加热电流对加热电阻的影响最大,进给量的影响最小。
(2)利用加热电阻经验公式对EHM加热电阻焦耳热所产生的温升进行有限元仿真的结果表明,加热电流大于100A时,切削区材料的平均温升随着加热电流的增大而迅速增大。根据仿真结果归纳出EHM工件材料初始温度的经验公式。
(3)使用EHM三维正交切削模型和Umbrello本构方程,对EHM的切削力和温度场分布进行三维有限元仿真的结果表明,EHM加热电流I≥160A可以得到较小的切削力;EHM切削变形区的切屑处会出现切削区的最高温度;对应最佳切削温度的EHM最佳加热电流为168~190A。
[1]叶邦彦,周泽华.难加工材料导电加热切削机理的研究[J].华南理工大学学报(自然科学版),1994,22(5):93-99.
[2]叶邦彦.导电加热切削最佳加热电流的确定及其控制[J].机械开发,1996,25(3):26-29.
[3]吴拓.利用导电加热切削改善已加工表面质量的研究[J].肇庆学院学报,2001,22(2):18-21.
[4]赵学智,叶邦彦,陈统坚.导电加热切削中切削区加热电阻的检测及特性[J].华南理工大学学报(自然科学版),2009,37(2):7-13.
[5]赵学智,叶邦彦,陈统坚.导电加热切削切削区加热电阻模型及试验分析[J].机械工程学报,2009,45(1):115-123.
[6]Kainth G S,Chaturvedi M N.Theoretical Investigation of Temperature in Hot Machining[J].International Journal of Machine Tool Design and Research,1975,15(4):241-256.
[7]徐兰英.难加工材料小孔导电加热钻削机理的研究[D].广州:华南理工大学,2009.
[8]Braunovic M,Myshkin N K,Konchits V V.Tribology of Electrical Contacts[M].Boca Raton,USA:CRC Press,2006.
[9]Astakhov V P.Tribology of Metal Cutting[M].London:Elsevier Science,2006.
[10]陈日曜.金属切削原理[M].北京:机械工业出版社,1994.
[11]Umbrello D,Hua J,Shivpuri R.Hardness - based Flow Stress and Fracture Models for Numerical Simulation of Hard Machining AISI 52100 Bearing Steel[J].Materials Science and Engineering A,2004,374(1/2):90-100.
[12]Holm R,Williamson J B P,Holm E.Electric Contacts:Theory and Application[M].4ed.New York:Springer,1999.
[13]吴拓,叶邦彦,赵学智.利用导电加热切削抑制积屑瘤和鳞刺的研究[J].工具技术,1998,32(12):8-10.

