罩式退火炉炉台密封圈的有限元分析

祁卫东，宋锦春

(1.东北大学机械工程与自动化学院，辽宁 沈阳 110004;2.宝钢集团有限公司，上海 201900)

0 引言

罩式退火炉是冷轧薄板特别是一些高性能的产品进行退火生产的主要设备之一。宝钢在80年代引进的氮氢罩式炉结构比较简单，技术水平相对比较落后。近年来，随着炉台设备的老化，钢卷的氧化色缺陷和出炉氧化问题日趋增加。通过分析，发现氮氢保护气体中的O2、CO2及H2O等氧化性介质含量较大时，钢卷退火就会发生表面氧化，而炉台密封失效是造成这一结果的主要原因之一。现场检查的结果表明，炉台密封圈处产生气体渗漏成为外部空气渗入炉内的唯一途径。由于罩式退火炉的工作温度较高，退火时间较长，温差较大，且密封圈承受的压力较大，密封圈在热应力和结构应力的作用下很容易发生疲劳失效。目前宝钢罩式退火炉采用国产密封圈，对密封圈的使用更换完全依靠经验，因此有必要对炉台密封圈的更换制定一定的标准。另外，即使炉台密封圈未失效，如果因密封圈的材料性能不够好，密封效果不理想的话，当炉内产生负压区时，也会造成炉外气体渗入炉内［1-2］。

鉴于以上分析，本文采用有限元分析软件ANSYS对炉台密封圈进行有限元分析，找出密封圈老化失效的原因机理，以便选用更合适的密封材质或改进密封圈的结构，达到强化密封效果的目的［3］。

1 有限元模型的建立

罩式炉的炉台环形密封圈的几何形状、热力学边界条件都是对称于中心轴的，同时物理系数是各向同性的。在理想情况下，密封圈沿轴线方向的载荷也是轴对称的。因此，可以把对密封圈的研究由三维问题简化为二维问题，只需研究坐标平面XOY上的截面部分。

炉台环形密封圈的失效主要发生在密封圈与内罩的接触面以及密封圈与安装槽的接触面上。由于密封圈相对内罩和安装槽来说是柔性体，其它的都是刚性体，而密封圈在被施加载荷之前已经在安装槽内有一定的压缩量，为了方便计算，可仅对环形密封圈进行分析。

环形密封圈的截面外径大于密封圈槽的直径，故密封圈安装之后会有一定的压缩量，且密封圈与安装槽接触的部分近似不可动，故为计算方便可设置该部分密封圈的边缘部分为全约束;同时，密封圈的上表面L2和L3则与内罩刚体L1相接触，且接触面随L1的位移其面积发生变化，该问题属于接触问题，故需设置L2和L3与L1为一个接触对。据此可建立环形密封圈的有限元分析模型如图1所示，经过网格划分后的模型如图2 所示［4-8］。

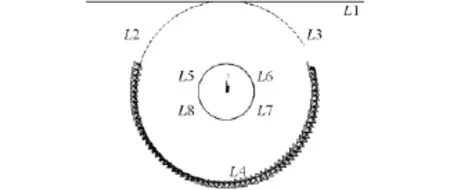
图1 环形密封圈模型Fig.1 Model of round seal ring

2 有限元分析

根据炉台密封圈的实际工作条件，在对其进行热－应力耦合分析时，按照载荷的加载顺序，可把载荷分为三个载荷步:(1)密封圈首先由于内罩的压力作用而受到5 mm的位移载荷，同时还受到密封圈中心的空腔里的空气作用在密封圈截面内径上的0.1 MPa的压力载荷。该载荷步所用的时间为0.01 h。(2)密封圈左侧边缘L2受到内罩外的0.1 MPa气体压力作用，而L3上承受的保护气体压力相对较小，可忽略不计。该载荷步所用的时间为0.01 h。(3)在前两步的基础上，密封圈底部L4因受到冷却水冷却而作用有30℃的温度载荷，密封圈上沿L2和L3的温度载荷与内罩的温度变化一致，如图3所示。

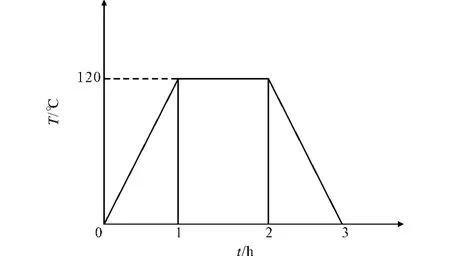
图3 密封圈上沿的温度变化Fig.3 Temperature variation of seal ring's top edge

对橡胶一类的超弹性体进行非线性分析，目前应用比较普遍和行之有效的方法是Mooney-Rivlin理论，对于罩式退火炉的炉台密封圈的有限元分析，可选取基于统计热力学的Neo-Hookean应变能函数，它是当Mooney-Rivlin模型的两个主要材料常数C1和C2中的C2为0时的一种特殊类型。该模型和材料的应变能偏量部分有关的材料常数可由从实验获得的经验公式中根据橡胶材料的硬度 (或弹性模量)计算得出［9-10］。本文中对炉台环形密封圈进行分析所选的密封圈参数见表1，其材料常数是见2和见3。其他参数:橡胶泊松比为0.499 99，密度为1 106 kg/m3，摩擦系数为0.2，比热为1 785 J/kg.K，导热系数为0.359 W/m.K。

表1 炉台环形密封圈参数Tab.1 Parameters of round seal ring for coil base

表2 橡胶在不同温度下的线胀系数Tab.2 Linear expansion efficient of rubber under different temperatures

表3 橡胶在不同温度下的Neo-Hookean常数Tab.3 Neo-Hookean constants of rubber under different temperatures

下面分四种模型进行热－应力耦合有限元分析，模型1的密封圈截面内径为8 mm，模型2的密封圈截面内径为10 mm，模型3改变模型2的材料Neo-Hookean常数见表4，模型4的密封圈截面内径为6 mm，材料的Neo-Hookean常数见表4。

表4 橡胶在不同温度下的Neo-Hookean常数Tab.4 Neo-Hookean constants of rubber under different temperatures

根据以上分析和参数的设定，对模型1的炉台环形密封圈进行轴对称问题热－应力耦合非线性有限元分析的结果如图4～9所示。(限于文章篇幅，对模型2～4不再给出具体分析过程)

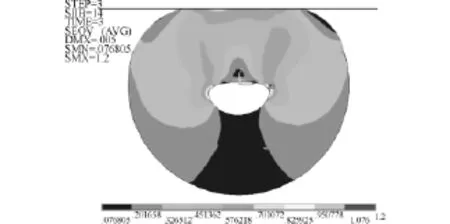
图4 密封圈von Mises应力分布图Fig.4 Von Mises stress distribution of seal ring

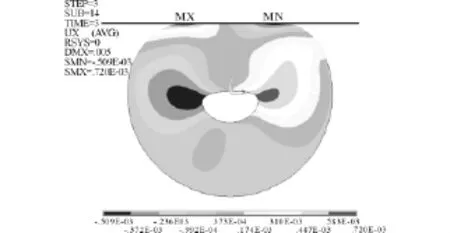
图5 密封圈X方向的位移Fig.5 Displacement of seal ring in X direction

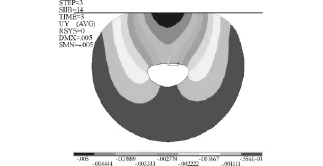
图6 密封圈Y方向的位移Fig.6 Displacement of seal ring in Y direction

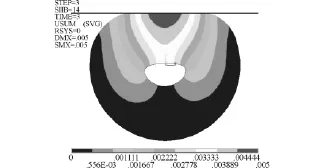
图7 密封圈总位移矢量Fig.7 Total displacement vector of seal ring

图8 密封圈综合剪应力Fig.8 Comprehensive shear stress of seal ring

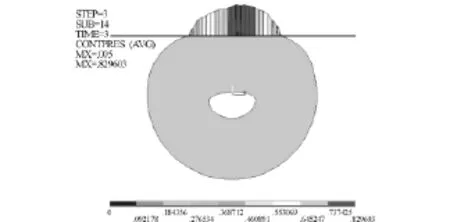
图9 密封圈接触压力Fig.9 Contact pressure of seal ring

3 结果分析

通过对模型1～4进行有限元分析，得到各模型分析结果的主要参数对比见表5。

表5 各模型的主要参数对比Tab.5 main parameter contrast of each model

通分析以上结果可得:

(1)由图4可见，炉台环形密封圈在热、位移及压力载荷的共同作用下，其内部的应力分布不均匀，密封圈上半部分应力较大，而下半部分应力较小。同时，在密封圈与内罩接触的面上出现应力集中区，此处的应力值达到0.701 072 MPa，其周围的应力值也达到0.576 218 MPa。最大应力值出现在环形密封圈的中心孔的左右两个大变形区，该处应力值达到1.2 MPa。由于密封圈左边L2上受到大气压力的作用，使得密封圈左右两边承受的应力并不对称。

(2)由图5可见，由于L2上的大气压力的作用，密封圈上各处的X方向的位移差别也很大。最大位移发生在密封圈与内罩接触面上的最左端，此处的位移区域较大，几乎达到密封圈的对称中心。而接触面的最右端则由于不受气体压力作用而位移几乎为零。另外，在密封圈的中心孔左右两边，位移量的差别也很大，中心孔右边由于受到因L2上的大气压力的作用而引起的密封圈内部的挤压作用而发生较大位移，同时位移量向密封圈右边的全约束边界的边缘延伸，使得该处密封圈向外部延伸。

(3)由图6可见，由于受到内罩的压缩和L2上大气压力的作用，密封圈左右两边的Y方向位移量并不均匀，右侧边缘部分的位移量较小。整个密封圈的Y方向位移量从上往下逐渐减小，这与L4上的全约束条件是一致的。

(4)由图7可见，炉台密封圈的位移矢量是沿Y方向的，其图像与密封圈Y方向的位移大致相同，说明密封圈的位移主要发生在Y方向，这与实际情况是一致的。

(5)由图8可见，密封圈左右两边承受的剪应力差别很大，右边的剪应力较大，最大值达到0.402 003 MPa。

(6)由图9可见，密封圈的最大接触压力为0.829 603 MPa，主要分布在中心线偏右侧。

(7)根据模型1的分析结果可见，密封圈与内罩的接触面上出现相对较大的应力集中，且接触面左侧因受到气体压力的作用而出现较大的位移量，该位移量引起密封圈内部应力和剪应力的分布都不均匀，密封圈右侧的X方向变形量、应力、剪应力都较大，而最易出现破坏的地方在于接触面上应力集中的区域和密封圈右侧与安装槽相接触的端点处，而又数前者的危险最大。

(8)通过模型2与模型1的分析结果对比可见，模型2与模型1的应力分布等基本一致，模型1的密封圈X方向的位移量较小，而接触压力较大，从而密封性能更好;但其最大剪应力也较大，更易于破坏。

(9)通过模型3与模型2的分析结果对比可见，模型3的最大剪应力较小，不易于发生破坏;由于弹性增加而造成最大X方向位移较大、最大接触压力较小，不利于密封，这一点可以通过增大密封圈的压缩量，即增大L1的位移来解决。

(10)由表5可见，模型4的最大接触压力最大，而最大X方向位移最小，最大剪应力也相对较小，最大接触应力增加不大。其中，最大接触压力和最大X方向位移是对密封性能影响较大的参数。因此，模型4密封圈综合密封性能是以上四个模型中最好的。

4 结论

综合考虑以上4个模型的分析结果，得出如下结论:

(1)炉台密封圈内部应力分布不均匀，在密封圈与内罩接触处有应力集中;

(2)密封圈沿X方向的变形量较大，几乎达到密封圈的中心线处;

(3)密封圈与内罩接触处的左侧边缘处，以及密封圈右侧与安装槽的接触点处较易发生破坏而影响密封质量;

(4)密封圈的截面内径越小、材料弹性越好，则其综合密封性能越好，但是限于工艺需求，密封圈截面内径不能太小，材料弹性也不能过高;

(5)模型4的密封圈密封效果较好，建议现场采用这种截面内径较小而弹性较好的密封圈，以提高炉台密封质量。

［1］王长周.LOI氮氢罩式退火炉钢卷氧化原因研究［D］，沈阳:东北大学，2006.

［2］Ho E，Nau B S.Gas emission by permeation through elastomeric seals ［J］. Tribology Transactions，1996，39(1):180－186.

［3］张振秀，聂军，沈梅，等.ANSYS中超弹性模型及其在橡胶工程中的应用 ［J］.橡塑技术与装备，2005，31(9):1－5.

［4］彭向和，高芝晖，曾祥国.O形密封环的弹塑性大变形和循环松弛分析 ［J］.重庆大学学报，1998，21(2):47－50.

［5］陈国定，Haiser H，Haas W，Lechner G..O形密封圈的有限元力学分析 ［J］.机械科学与技术，2000，19(5):740－744.

［6］廖日东，左正兴，邹文胜.O形圈轴对称超弹性接触问题的有限元分析 ［J］.润滑与密封，1996(5):30－33.

［7］陈宏，左正兴，廖日东.橡胶密封圈三维接触问题的有限元分析［J］.兵工学报坦克装甲车与发动机分册，1999，(4):30－32.

［8］刘溪涓，刘承宗，林钧毅，等.一种含超弹性接触问题的密封结构的有限元求解方法 ［J］.中国机械工程，2001，12(11):1211－1213.

［9］王伟，邓涛，赵树高.橡胶Mooney－Rivlin模型中材料常数的确定 ［J］.特种橡胶制品，2004，25(4):8－10.

［10］赵林.О形密封圈的合理使用 ［J］.机械工程师，2004(5):85－86.