基于多子空间线性判别分析的特征提取与分类
董 琰
(中石化胜利油田分公司ERP支持中心,山东东营257000)
0 引 言
特征提取和分类始终是模式识别研究的重要课题,在生物特征识别,基因图谱分析,遥感影像分类,空间数据挖掘等应用领域更有着广泛的实用价值。随着数据的复杂性和规模急剧增长,特征提取和分类的难点主要表现为数据集中样本的特征维数远远大于每类样本数量。由于样本的稀疏造成样本类的统计特征描述不充分,在利用经典的线性判别分析方法 (LDA)进行分类时往往因类内散度矩阵的奇异性而无法求解,即模式识别中的高维小样本问题[1]。而实践中常用Fisherface方法来解决高维小样本问题[2],它由主成分分析 (PCA)和线性判别分析 (LDA)组成,先通过PCA实现降维,从而消除类内散度矩阵的奇异性并有效降低运算复杂度,但是PCA的作为最佳描述特征的提取方法是以投影后方差最大为准则,并没有判别分析能力,降维时没有考虑样本的类属信息,在维度缩减的同时,也带来分类判别信息的缺失。LDA的目标是使特征提取后的样本类间离散度和类内离散度的比值最大化,即各类样本在特征空间中有最佳的可分离性。该方法利用最大散度比准则将所有类的样本投影到同一个特征空间中,而忽略了各类样本在特征分布上的差异;同时,对于一个特定的模式识别问题,表达和识别模式的特征具有不同的形式,而且在物理意义上也不是完全相同的,并且在数量级也有很大差别,简单基于距离的匹配划分难以实现客观的分类判别。
本文针对常用PCA和LDA在降维和判别分析上的不足,在算法设计中,一方面借鉴了PCA在维数缩减上的作用,另一方面尽可能多地保留类的判别信息。算法的简单思想就是通过对每类样本进行特征提取以有效地保留判别信息和降维。提出的多子空间线性判别分析,对不同样本类分别描述,针对每类样本提取最适合分类的特征子空间;分类时综合考虑投影后样本的概率分布模型,以概率距离作为隶属置信度,并以此作为分类的依据,选取最可能的类属划分。
1 相关技术
LDA[3]是统计模式识别中最基本和常用的分类方法,其准则函数如下

LDA使用最大散度比准则,目的是求使准则Jd(w)最大的投影w,在此投影下可以使样本的类间散度矩阵Sb与类内散度矩阵Sw的比值最大,使得经过特征提取后的样本有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。当Sw非奇异时,根据Lagrange乘数法可得w是由矩阵S-1wSb的特征向量组成的矩阵,但在高维小样本的情况下,Sw非奇异的前提常常无法满足。
根据子空间分析理论,解决高维小样本问题的关键是去除由冗余特征组成样本空间的稀疏部分,这些冗余特征所具有的判别信息往往很少或没有,是类内散度矩阵奇异的根源,针对LDA方法在解决高维小样本问题的困境,先后 有 Fisherface (PCA + LDA),Direct-LDA[4], Dual-LDA[5],Generalized LDA[6]等方法提出,其中PCA+LDA作为有效的方法广泛应用在人脸识别领域。在PCA+LDA处理中,首先利用PCA进行维度缩减,作为一种全局提取技术,PCA的目标是寻找一组正交向量使得所有样本经过投影后的方差最大,而PCA在降维过程中并没有考虑样本的类别标志,因此在以分类为目标的特征提取技术中并不是最优的,提取后的特征反而可能弱化了原始数据的分类能力[7]。下面以2维两类分类问题为例,说明PCA在以分类为目标的场合下,作为特征提取手段的不足。
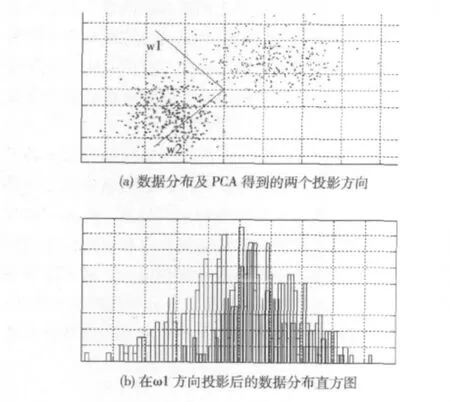
图1 PCA用于两类分类示例
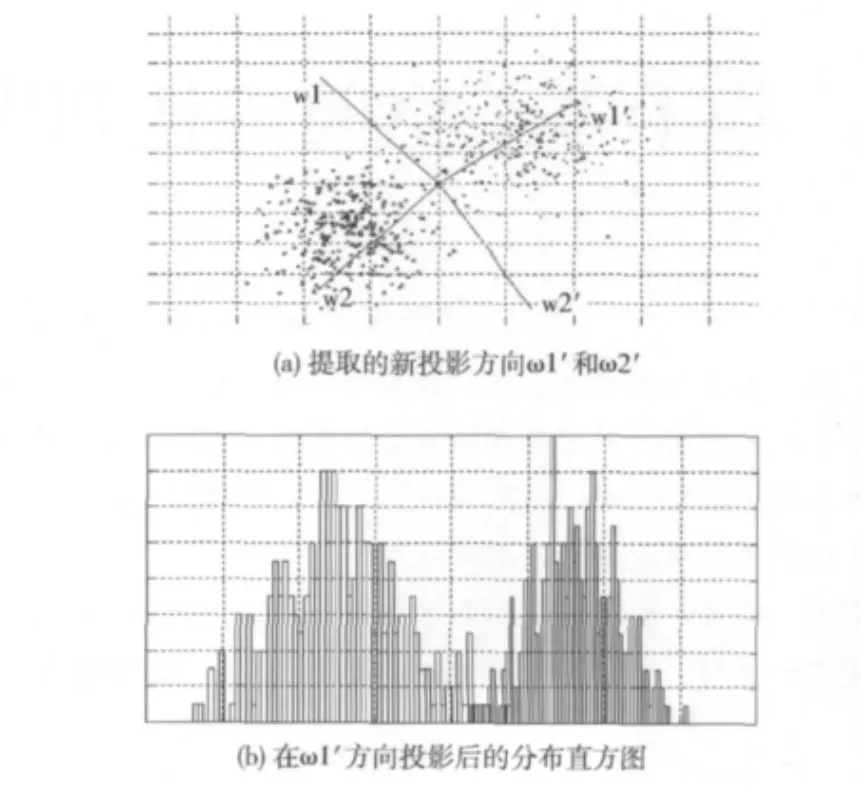
图2 考虑分类后的PCA及分类结果
图1 、图2中的浅灰和深灰 (其中图1(a),图2(a)中左下侧为浅灰,右上侧为深灰;图1(b),图2(b)中左侧浅灰,右侧深灰)分别代表不同类的数据样本,将样本数据分别投影到PCA第一主元方向ω1和新提取的投影方向ω1′,样本数据由2维降为1维。比较图1与图2降维后的数据直方图分布,可以看出在图2(b)中,两类数据在投影后得到更好的分离。由此可知PCA并不是面向分类的特征提取方法,一般情况下,由其得到的特征是最佳描述特征,而不是最佳分类特征。
2 算法提出
对于包含c类样本的分类问题,类中的所有样本是已知的对原始类最可能的描述。但是样本分类时,不仅依赖对类内共性的描述,更多的是依赖于对类间差异的描述。直观上,通过对每类单独描述,提取最能体现类内共性和类间差异的特征,可以提高对类模式描述的准确性和全面性,从而减小分类的错误。提出的算法分为2个步骤,即面向分类的特征提取和分类匹配,具体算法如下:
2.1 面向分类的特征提取
(1)computeSb
(2)initialize i=0
(3)for i=1+1
(4) computeSb-Swi
(5) compute eigenvectors toSb-Swi,return projection matrixWi
(6)until i=c
(7)returnW1,W2,…,Wc
(8)end
其中:Sb,Swi,Wi分别代表类间散度矩阵,第i类的类内散度矩阵以及用于特征子空间提取的投影矩阵,与经典的LDA最大散度比准则不同,每个投影矩阵的求解采用最大散度差准则

即求得使JF(w)最大的投影矩阵w,根据广义瑞利商极值特性,最优解是由矩阵Sb-Swi的前k个最大特征值对应的特征向量组成的投影矩阵。同传统的LDA相比,特征提取不需要对Swi求逆,有效地避免了因Swi奇异无法求解的难题,通过计算可以分别得到c个投影矩阵。
2.2 分类匹配
(1)initialize test samplex,i=0,feature subspace extraction matricesW1,W2,…,Wc
(2)for i=i+1
(3)projectxi=
(4) Initialize j=0
(5) for j=j+1
(6) calculate probability measurebetweenxiandrepresenting projection of classωjonto subspaceWi
(7) until j=c
(8)scan nearest measure over allcclasses in i-th subspace:J(i)=argma
(9)until i=c
(10)scan nearest measure over all c classes and c subspaces:I=argma
(11)returnI
(12)end
分类是通过两层遍历排序实现,内层遍历求得在某一特征空间内的分类匹配排序,外层遍历则求出在所有特征空间内的分类匹配排序,最终按照最大原则或者k紧邻原则判断测试样本的所属类别。与以往的基于距离的判别方法不同,在此按照贝叶斯规则[8],以概率距离作为对隶属置信度的衡量,判别时选择具有最高置信度的类别。概率度量d用于评价待测样本类别隶属的置信度,在此对类内样本的条件概率分布采用正态分布假设,即
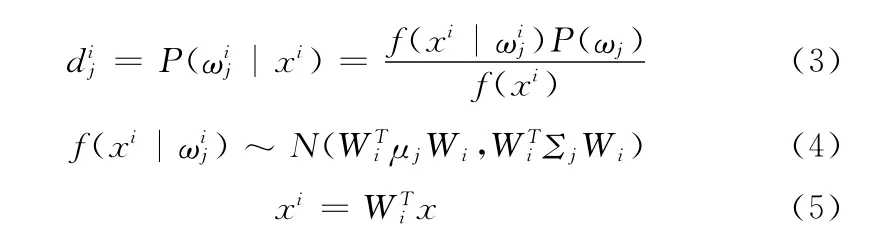
式中:Wi,,μj,Σj——第i类的投影矩阵和转置,以及第j类样本的均值向量和协方差矩阵。
3 试验与分析
实验数据来自于数据库UCI,选用的测试数据集描述如表1所示,其中Congressional Voting Records和Breast Cancer是简单数据,显而易见,分类的性能与训练样本数量和提取的特征数量有关。为了减小误差,实验采用10倍交叉验证进行评价。
为了对比算法性能,我们选择了线性判别方法:LDA和Fisherface[9-10]以及非线性判别方法:KPCA和KLDA作为比较对象。对比算法选择是基于可比性上的考虑[11],一方面选择的两种线性判别方法和提出的算法都是基于二阶统计特性,都需要计算样本的一二阶统计矩;除此之外三者子空间的提取都需要进行特征值分解而非其他复杂的线性分解技术;另一方面,作为一种拟合非线性判别分析的方法,与基于核方法的非线性判别分析KPCA和KLDA比较可以更充分说明问题。测试是在2.2GHz AMD CPU,1G内存的计算机上进行。结果列于表2,3,4;其中m代表提取特征的维数。
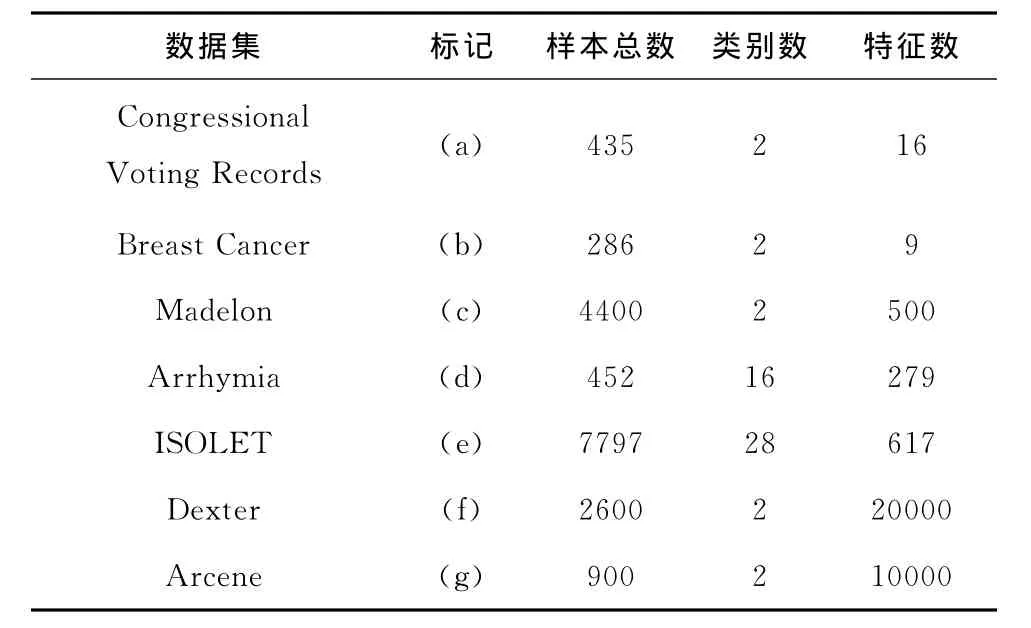
表1 测试数据集描述

表2 分类性能比较 (数据集a,b)
从表2可以看出在线性可分的测试集a和b上本文方法并没有突出优势,5种方法的性能差距<5%;从表3中可以看出,当原始特征维数增大后,KPCA和KLDA在分类性能提升明显;而在具有线性不可分的测试集f和g上,PCA和LDA由于线性判别的局限,效果并不理想;而KPCA也由于PCA的本质则更适合于特征描述而非分类,KLDA则在分类上优于KPCA;而本文的方法在平均处理时间上远低于KLDA和KPCA,且具有更高的分类识别率。

表3 分类性能比较 (数据集c,d,e)
在高维小样本分类问题中,尤其在生物特征的识别中,类模式往往是线性不可分的,更有效的是依靠非线性判别分析;然而在非线性判别分析中普遍存在着难以选择合适的非线性变换以及计算的高复杂性,这使得其在实际应用中受到限制。而提出的方法本质上是利用多线性判别分析分类分段拟合非线性判别分析,不但提高了分类的准确率而且保持了线性判别分析在计算上的简捷性,特别适合于存在类重叠的情形。另一个优于PCA、LDA等单子空间方法的方面在于其灵活性,在单子空间方法中特征空间中的特征向量维数是一致的,而在多子空间方法中可以根据每类样本的情况选择更适合的向量维数。算法存在的不足在于计算复杂度与类的数量c有关,特别是对每一个测试样本都需要进行c2次概率距离计算。
4 结束语
使用PCA方法和LDA方法都能大大降低原始特征空间的维数,结合这两种方法Fisherface方法已在人脸识别中得到了的应用;然而PCA方法得到的特征是最佳描述特征而不是最佳分类特征,LDA方法则难以处理类重叠。本文提出的方法首先利用最大散度差准则对每类样本进行线性判别分析,通过特征值分解获得各类的投影矩阵,从而可以获得面向分类的最佳描述特征,最后利用贝叶斯判别得到最高隶属置信度作为判别依据。这样,既利用了线性判别分析方法的线性计算的优点,又弥补了它们在处理类重叠和线性不可分上的不足,同时使分类器的设计更加简洁、有效,提高了对高维复杂数据的识别率。

表4 分类性能比较 (数据集f,g)
[1]Koel Das,ZoranNenadic.An efficient discriminant-based solution for small sample size problem [J].Pattern Recognition,2009,42(5):857-866.
[2]ZHU Minghan,SHAO Xiangyi.Based on the vector group Fisher linear discriminant analysis method [J].Computer Engineering and Applications,2011,47 (6):205-207 (in Chi-nese).[朱明旱,邵湘怡.基于向量组的Fisher线性鉴别分析方法 [J].计算机工程与应用,2011,47 (6):205-207.]
[3]SHI Jin,HU Ming,SHI Xin.Text segmentation based on model LDA [J].Chinese Journal of Computer,2008,31 (10):1865-1873 (in Chinese).[石晶,胡明,石鑫.基于LDA模型 的 文 本 分 割 [J]. 计 算 机 学 报,2008,31 (10):1865-1873.]
[4]LIU Jin,ZHANG Junying,ZHAO Feng.Radar HRRP target recognition in amplitude spectrum subspace based on direct LDA[J].Journal of Systems Engineering and Electronics,2008,30(10):1815-1818 (in Chinese). [刘敬,张军英,赵峰.基于direct LDA的幅度谱子空间雷达目标识别 [J].系统工程与电子技术,2008,30 (10):1815-1818.]
[5]WU Ting,CHENG Yaqi,ZHANG Yanjun.Improved real-time anti-aliasing perspective shadow maps algorithm and its implementation[J].Computer Engineering & Design,2011,32(10):3435-3437 (in Chinese). [吴婷,程亚奇,张延军.改进的实时反走样透视阴影图算法及实现 [J].计算机工程与设计,2011,32 (10):3435-3437.]
[6]ZHAO Chuanqiang,WANG Huiyuan.Face recognition method using improved D-LDA based on DCT [J].Computer Engineering and Applications,2007,43 (20):245-248 (in Chinese). [赵传强,王汇源.一种基于DCT的改进D—LDA人脸识别算法[J].计算机工程与应用,2007,43 (20):245-248.]
[7]Myoung SooPark,JinYoungChoi.Theoretical analysis on feature extraction capability of class-augmented PCA [J].Pattern Recognition,2009,42 (11):2353-2362.
[8]DENG Haisong,MA Yizhong,SHAO Wenze.Research on meta-modeling using bayesian hierarchical priors [J].Journal of System Simulation,2011,23 (11):2291-2295 (in Chinese).[邓海松,马义中,邵文泽.基于贝叶斯多层先验的元建模研究 [J].系统仿真学报,2011,23 (11):2291-2295.]
[9]WANG Huize,GONG Shengrong,LIU Chunping.Fisherfaces based on fusion of global and local features[J].Computer Engineering and Applications,2008,44 (24):194-196 (in Chinese). [王慧泽,龚声蓉,刘纯平.融合全局和局部特征的Fisherfaces方法 [J].计算机工程与应用,2008,44 (24):194-196.]
[10]ZHAO Song,PAN Ke,ZHANG Peiren.Face recognition using face symmetry:Symmetrical Fisherface[J].Journal of University of Science and Technology of China,2009,39(11):1183-1188 (in Chinese). [赵松,潘可,张培仁.对称性在人脸识别中的应用:对称Fisherface[J].中国科学技术大学学报,2009,39 (11):1183-1188.]
[11]Dacheng Tao.Discriminative linear and multilinear subspace methods[D].School of Computer Science and Information Systems,Birkbeck College,University of London,2009.

