软件风险评估量化分析研究

闫秋粉，南振岐，姚尔果，薛小虎

（1.西北师范大学 数学与信息科学学院，甘肃 兰州730070；2.新疆乌鲁木齐市军区测绘信息中心，新疆 乌鲁木齐830000）

0 引 言

风险是介于确定性和不确定性之间的状态，是指未来的消极结果或损失的潜在可能。采用传统的基于数学模型的风险评估方法［1－4］对评估结果的判定会产生较大的模糊性和主观性，通过对软件风险评估过程分析，提出了风险评估指标体系模型，运用模糊数学理论实现了对软件风险评估因素的量化。

BP（back propagation）神经网络通常采用梯度下降法，极易陷入局部最优值，收敛速度慢。粒子群优化算法（particle swarm optimization，PSO）是一种基于群体相互协作的智能优化算法，通过粒子群进化速率改进粒子群算法（dynamic particle swarm optimization，DPSO），提出惯性权重因子随每次迭代的搜索步长动态变化的方法，增强了全局搜索能力，提高了收敛的精度和速度。通过DPSO算法训练BP神经网络构建了进化神经网络模型，最后实例验证了基于进化神经网络模型的软件风险评估方法可实现对风险因素的量化评估，为决策者及时采取风险规避措施提供了客观依据，极大地减少了软件风险带来的损失。

1 软件风险评估

风险评估为风险管理［5－6］的重要环节，其过程见图1。

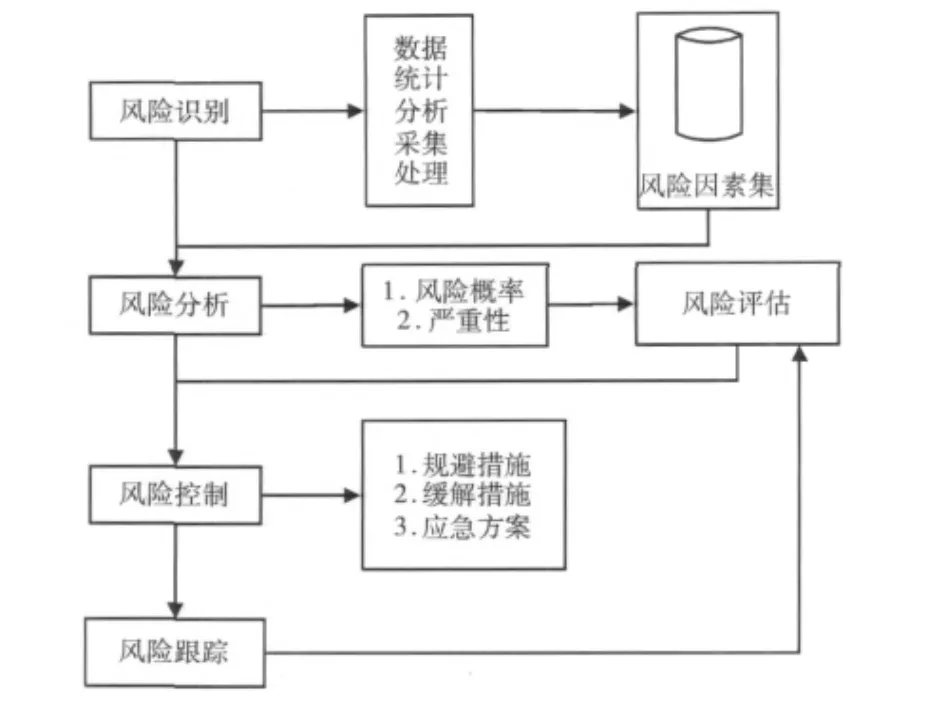
图1 风险评估过程

（1）风险识别：根据软件项目本身复杂性和内外部环境，结合风险知识库，识别主要的风险源，统计风险因素集。

（2）风险分析：根据已辨识的风险源发生的概率和严重性初步估算风险系数。

（3）风险控制：针对风险评估中风险系数超过规定范围的高风险项进行风险控制，制定规避措施，如若规避不成功，实施缓解措施，同时对较高风险因素制定应急方案。

（4）风险跟踪：定期关注风险状态，对已有的风险因素重新评估风险系数，同时识别新的风险源，制定风险措施。

通常风险量化［7－8］是指发生潜在损失的可能性与潜在损失两者的乘积，Boehm将之称为风险暴露，其关系为：RE＝P（UO）×L（UO），其中，RE为风险暴露，P（UO）为结果不满意的概率，L（UO）为由于结果不满意而给被影响方造成的损失。该风险模型存在的问题 “低概率，高损失”与 “高概率，低损失”的风险在数值上的表现是一样的。针对此问题，本文提出了风险评估指标体系，并定义了指标函数进行量化，结合粒子群算法改进BP神经网络模型，提出了基于进化的神经网络的软件风险定量评估模型，经仿真结果表明该模型对实际评估拟合性较好。

2 软件风险评估指标评判体系及评估模型的构建

基于风险管理的角度提出风险评估指标体系模型，将风险分为三类进行处理 （如图2所示）：发生概率高且产生影响大的风险作为最高级别风险，重点关注的风险；发生概率高但影响程度中到低的风险；高影响但风险发生概率低的风险为可忽略的风险。

2.1 软件风险评估指标评判体系的构建

本文提出的软件风险评估指标评判体系是从风险管理的角度构建而成，如表1所示。

定义1 产品规模风险RPS＝ ｛r1，r2，r3｝：

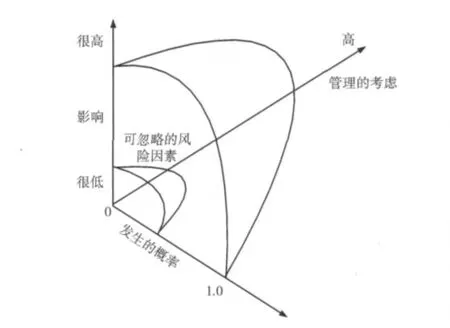
图2 风险管理分布概率

表1 风险评估指标体系

（1）规模估算偏差风险是指实际用例点数与估算用例点数间的偏差风险。r1＝∑ （AUC－EUC）／AUC×WUC，WUC为用例的平衡因子。

（2）技术复杂度风险，考虑了系统性能要求，内部处理复杂度以及复用程度等。为技术复杂度风险因素值，WiTF为该因素值的平衡因子。

（3）环境复杂度风险，是指项目开发过程中的硬件资源以及软件资源的不可用性风险。为环境复杂度风险因素值，为该因素的风险平衡因子。

定义2 相关干系人风险RS＝ ｛r4，r5，r6｝：

干系人风险包括内部干系人风险和外部干系人风险。

（1）开发人员数目及经验风险为内部干系人风险，直接关系着软件项目的质量和生产率。r4＝PN×WPN＋TE×WTE＋CC×WCC，PN为人员在项目开发过程中的架构分布，TE为团队开发经验，CC为团队遵守开发准则的复杂度，∑WPN＋WTE＋WCC＝1为各自的相关平衡因子。

（2）高层管理者决策风险为内部干系人风险，是指管理者在决策时选择最优决策产生的风险与选择当前决策产生的风险偏差。r5＝ （DMmax－CDM）／DMmax×WDM，DMmax为最优决策的风险，CDM为当前决策风险，WDM为决策平衡因子。

（3）客户特性风险为外部干系人风险，是指客户代表所做的需求模糊风险和不参与同行评审产生的风险。r6＝RF×WRF＋PR×WPR，RF为需求模糊风险，PR为不参与同行评审风险，∑WRF＋WPR＝1为各自的平衡因子。

定义3 过程风险RP＝ ｛r7，r8，r9｝：

（1）成本风险是指由于估算经验不足及使用的估算方法不成熟造成的实际消耗成本与估算成本偏差。r7＝EE×WEE＋EM×WEM＋CV×WCV，EE为估算经验不足造成的风险，EM为估算方法不成熟造成的风险，CV为成本偏差率，∑WEE＋WEM＋WCV＝1为各自的平衡因子。

（2）进度风险是指由于项目经理经验不足安排进度计划不合理和人员开发技术经验不足造成的风险。r8＝PME×WPME＋DE×WDE＋SV×WSV，PME为项目经理开发经验不足的风险，DE为开发人员技术经验不足的风险，SV为进度偏差率，∑WPME＋WDE＋WSV＝1。

（3）性能风险是指产品能够满足需求且符合于其使用目的的不确定的程度。

r9＝ （RFM－AFM）／RFM×WFM，RFM为需求功能模块，AFM为实际功能模块，WFM为平衡因子。

定义4 风险性能RRP＝ ｛r10，r11｝：

已识别风险 （identifiedrisk，IR）：是指目前没有发生但已识别出的风险，后期存在发生的可能性。

规避成功 （avoidsuccessrisk，ASR）：是指风险已识别，采取了规避措施，后期没有发生。

规避失败 （avoidfailurerisk，AFR）：是指风险已识别，采取了规避措施，但后期该风险仍然发生。

未识别风险 （unidentifiedrisk，UR）：是指风险未识别出，风险系数较小，后期项目中该风险发生，但对项目影响不大。

异常 （exception，E）：是指风险未识别出，风险系数较大，后期项目中该风险发生时对项目有较大影响。

风险总数 （risktotal，RT）：RT＝IR＋ASR＋AFR＋UR＋E。

（1）不可识别性风险指未识别风险与异常占风险总数的比例，r5＝ （UR＋E）RT。

（2）不可控制性风险是指规避失败风险占已识别风险、规避成功风险与规避失败风险三者之和的比例，r5＝AFR／（IR＋ASR＋AFR）。

2.2 软件风险评估风险等级划分

风险指标的风险等级划分为5个等级，如表2所示。

表2 风险等级划分

3 基于改进DPSO算法的BP神经网络模型

3.1 BP网络结构

BP神经网络是采用反向传播误差调整的学习方法，本文采用三层前馈神经网络，如图3所示。其基本思想是输入层为经预处理的风险指标，经隐含层的训练，输出系统的风险评估等级；隐含层用Sigmoid函数作为传递函数

输入层与隐含层的映射关系y0i＝C （X0i，Wji）。

隐含层与输出层的映射关系yk＝ （Wji，y0i，λ）。

输出信息与期望目标之间的误差e为

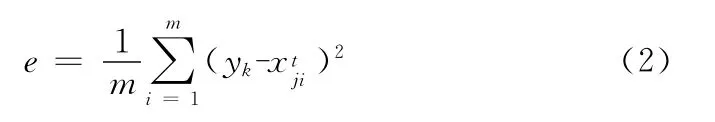
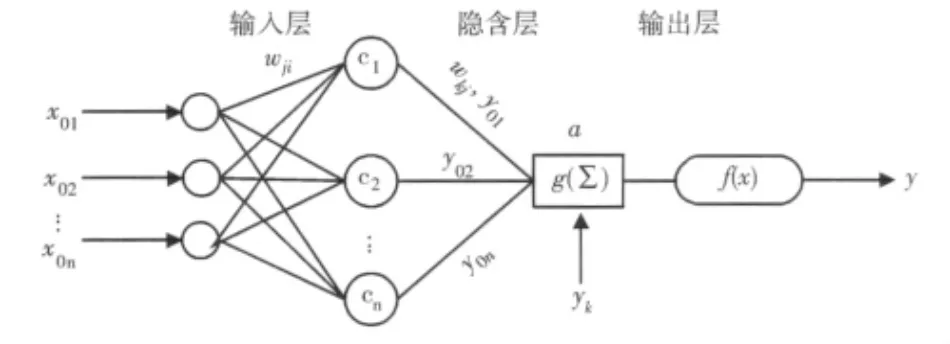
图3 BP神经网络模型

3.2 粒子群算法

粒子群优化算法为Kennedy和Eberhart两位博士于1995年基于鸟群觅食行为而提出的群体智能算法。此算法描述如下，作为本文的标准粒子群算法

式中：、——粒子i在第k次迭代中的速度向量和位置向量；c1、c2——学习因子；r1、r2—— ［0，1］之间的随机数；pbestij、gbestij——粒子的个体最优值和群体最优值；w——惯性权重因子平衡局部最优和全局最优。

3.2.1 改进的粒子群算法

在标准PSO算法中，每一个粒子都会向最好位置的方向聚集，导致搜索空间的多样性缺失，适应值停滞。文献［9］引入聚焦距离变化率的概念，将惯性因子表示为聚焦距离变化率的函数，从而动态改变惯性权重。文献 ［10］采用自适应均衡法调整惯性权重因子，通过压缩因子k逐渐减小w。本文在改进的DPSO中，提出粒子群进化速率，反映了粒子进化速度，使w值根据粒子进化速率动态变化，粒子i在第t次与第t＋1次迭代中随搜索的空间步长动态变化。

本文提出的粒子进化速率φ（t）直观地反应了粒子i在搜索位置上进化的程度，表示了粒子的目前位置与收敛位置之间的差异，如图4所示。

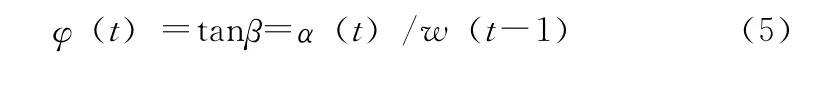
图4 粒子进化速率

当φ（t）＞1时，说明本次迭代发散，要求搜索步长增大以加强全局寻优能力。当0＜φ（t）＜1时，说明本次迭代收敛，要求搜索步长减小以加快粒子的聚集度加强剧本寻优。而当经过若干次迭代后，φ（t）保持值为0时，说明粒子已经找到了最优值或者算法停滞。

改进的惯性权重w按照下式变化

式中：f（xi（t））——第i个粒子在第t次迭代时对应的函数值：f（xi（t））＝f（xi，1（t），xi，2（t），…xi，k（t））。f（xbest（t））——最优粒子在第t次迭代时对应的函数值：f（xbest（t））＝minf（xi（t））。

3.2.2 算法测试

本算法DPSO与标准粒子群算法PSO相比较，测试该算法的优越性。以Sphere函数和Rastirgrin函数为基准测试函数，进行最小值寻优。维数为20维，参数设置如下：两种算法粒子群规模为40，学习因子c1＝c2＝2最大迭代次数1000。

表3给出了实验结果，图5与图6分别给出了Sphere函数和Rastirgrin函数随迭代次数增加函数收敛变化图。

表3 测试结果

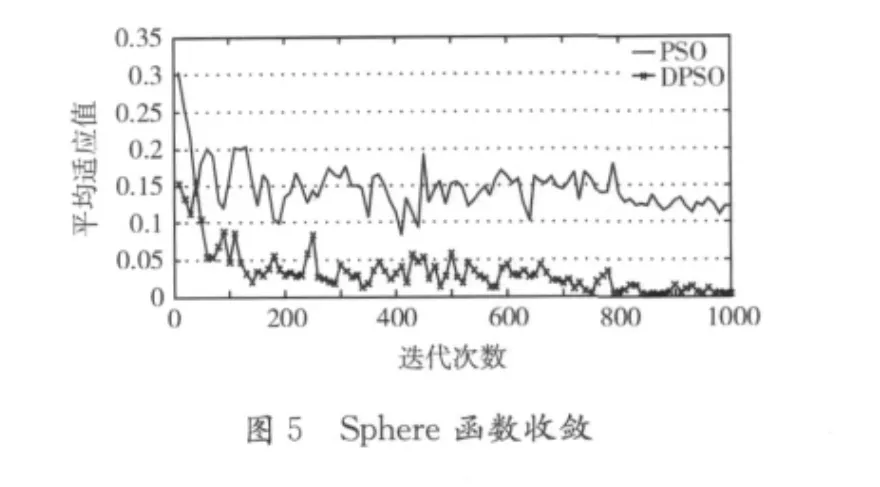
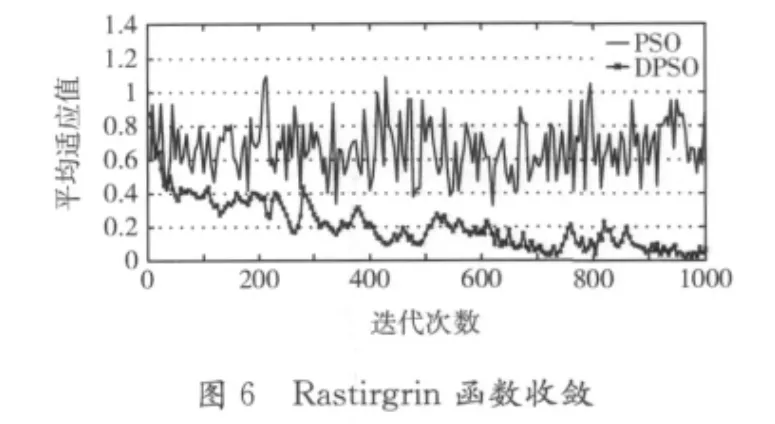
由图5和图6可以看出，DPSO算法具有更快的收敛性，其曲线基本趋于单调下降状态，而标准PSO算法上下波动幅度较大，多次出现水平不变。由此，改进的PSO算法不易陷入局部最优，可以进行全局寻优，寻找全局最优点。

4 基于DPSO－BP神经网络的软件风险评估模型的步骤及应用

风险因素集R＝ ｛r1，r2，r3…rn｝，对于ri∈R，按第i个属性进行评估，得到ri的评估值rij，从而构成模糊隶属度矩阵

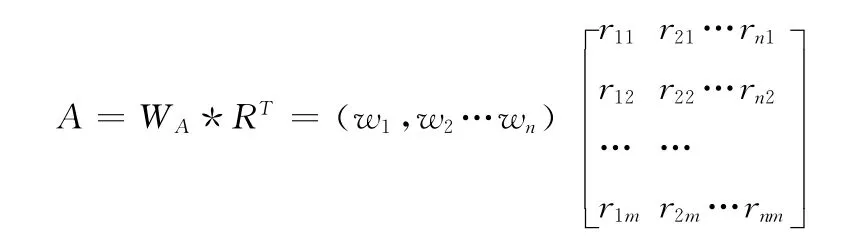
神经网络输入与输出层权值Wji和Wkj，学习样本Xi，期望输出值yk，输出值与期望目标之间的误差为e（xi），网络模型训练后的预设精度δ＝10－3。学习因子c1＝c2＝2，粒子群规模为N，搜索空间维数为D，迭代次数为iter，当前迭代次数t，搜索步长为η，粒子群训练后的预设精度γ＝10－6。粒子位置xij∈ ［－1，1］，粒子速度vij∈ ［－10，10］。

输入：A＝ ｛A1，A2，A3…A11｝。

输出：yk。

步骤1：初始化。c1＝c2＝2，N＝11，D＝40，iter＝500，η＝0.01。

步骤2：根据式 （2），经t次训练输出误差e（xi）。

步骤3：误差e（xi）作为粒子群的适应度值fitness＝e（xi），比较适应度值，记录每个粒子的历史最优位置和粒子群历史最优位置。

步骤4：根据式 （5），（6），（7）更新粒子位置和速度，若xij［－1，1］｜｜vij［－10，10］，转步骤4。

步骤5：若fitness≥δ｜｜t＝iter，Wji＝gbestmi，Wkj＝gbestnj。否则转步骤6。

步骤6：若e（xi）≤γ，算法结束，否则转步骤3。

将所在公司的10个评估试点项目数据作为训练样本，利用本文提出的软件风险体系评估模型进行风险评估，如表4所示。

表4 风险评估列表

经预处理后的风险指标因素值如表5所示。

表5 风险因素值

神经网络模型输出结果与实际结果间的误差变化如图7所示，经过进化网络模型输出的结果在55次迭代中就已经达到了预设的精度，最小误差达到了4.3826E－08，平均误差为0.1364E－04。

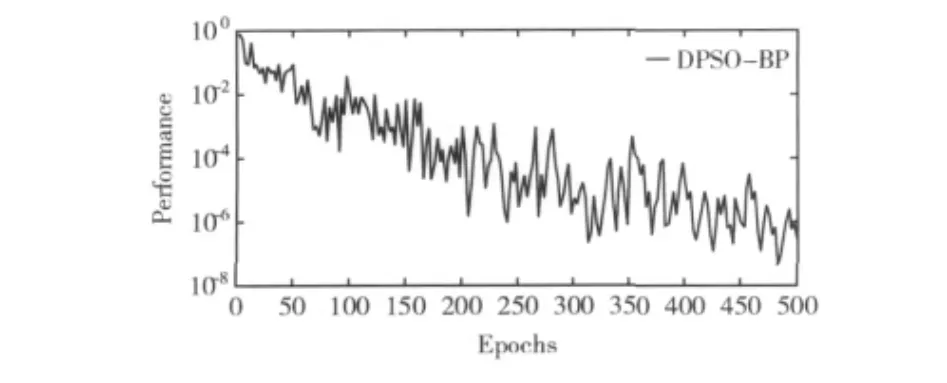
图7 误差变化

结果分析：采用本文构建的风险评估指标体系与依靠传统的专家打分相比，风险值评估结果合理，能够对发生的风险进行比较精确的评估。同时运用改进粒子群算法训练BP神经网络，减小了误差值，提高了模型的评估能力，为项目中及时调整项目计划，制定风险缓解措施，达到减少风险损失的目的起到了指导性作用。

5 结束语

本文提出了风险指标体系以及将风险值量化的方法，减少了凭借专家评估的模糊性和主观性，与定性分析和完全依靠专家评分相比较，数据比较客观。结合风险不确定性、非线性等自身特点构建的基于进化神经网络模型的软件风险定量评估模型，通过智能学习算法训练神经网络精度，与传统模型相比，有较好的性能，最后通过实例仿真结果表明此模型的评估结果比较客观。

［1］Iranmanesh H，Nazari Shirkouhi S.Risk evaluation of information technology project based on fuzzy analytic hierarchal process ［J］.World Academy of Science Engineering and Technology，2008，40 （2）：351－357.

［2］Avner Engel，Mark Last.Modeling software testing costs and risks using fuzzy logic paradigm ［J］.Journal of Systems and Software，2007，80 （6）：817－835.

［3］Reyes，Cerpa，Vejar.The optimization of success probability for software projects using genetic algorithms ［J］.Journal of Systems and Software，2011，84 （5）：775－785.

［4］DING Jianjie，HAO Kegang，HOU Hong，et al.Research of software project risk management based on set theory ［J］.Computer Science，2010，37 （4）：117－119 （in Chinese）. ［丁剑洁，郝克刚，侯红，等.基于粗糙集的软件项目风险管理研究 ［J］.计算机科学，2010，37 （4）：117－119.］

［5］Latifa Ben Arfa Rabai，Yan Zhi Bai，Ali Mili.A quantitative model for software engineering trends ［J］.Information Sciences，2011，181 （22）：4993－5009.

［6］Paul L Bannerman.Risk and risk management in software projects：A reassessment［J］.Journal of Systems and Software，2008，81 （12）：2118－2133.

［7］Lars Grunske，David Joyce.Quantitative risk－based security prediction for component－based systems with explicitly modeled attack profiles ［J］.Journal of Systems and Software，2008，81（8）：1327－1345.

［8］WANG Changfeng，WANG Hualan.Theoretical model for the security risk quantitative analysis of large software R＆D projects ［J］.J Tsinghua University （Natural Science），2009，49（S2）：2103－2107 （in Chinese）.［王长峰，王化兰.大型软件研发项目安全性风险定量分析理论模型 ［J］.清华大学学报（自然科学版），2009，49 （S2）：2103－2107.］

［9］REN Zihui，WANG Jian.New adaptive particle swarm optimization algorithm with dynamically changing intertia weight ［J］.Computer Science，2009，36 （2）：227－256 （in Chinese）.［任子晖，王坚.一种动态改变惯性权重的自适应粒子群算法［J］.计算机科学，2009，36 （2）：227－256.］

［10］Ali T Al－Awami，Azzedine Zerguine.A new modified particle swarm optimization algorithm for adaptive equalization ［J］.Digital Signal Processing，2011，21 （2）：195－207.