利用图像熵识别纸币扎把

张利明，范瑞春，赵喜清

（1.河北北方学院信息科学与工程学院，河北 张家口075000；2.中国农业银行股份有限公司张家口分行信息技术管理部，河北 张家口075000）

0 引 言

纸币管理是国内银行金融业的一项重要业务。目前，中国经济迅猛发展，纸币发行量逐年增多，致使银行及各级货币处理中心处理纸币的工作量逐年增大，但国家信用制度还不完善，而要求银行工作零差错，这就要求纸币处理的每一个环节（包括检伪、清分、清点、扎把、捆扎、塑封）都要严格把关。而纸币扎把的识别又是一个关键环节。纸币捆钞设备设计单位提出在捆钞机中附加纸币扎把识别功能，从而完善银行纸币管理。而其中对纸币图像处理的关键技术就是对纸币扎把的识别。由于纸币管理的严格性，在识别过程中如何提高识别率，特别是能够在实际环境中面对随机噪声的干扰如何达到几乎百分之百的识别率是提高识别速度一个需要认真研究的重要问题。

1 研究现状

目前纸币识别中扎把处理方式主要有两种，第一种方法是扎把图像颜色识别法，就是通过扫描扎把颜色来区分扎把，这种方式的缺陷在于必须保证扎把的颜色与背景色有非常大的区分且扎把的颜色一致。

第二种方法是图像噪声边沿法。对扎把图像通过平滑噪声来消除图像噪声点以平滑图像，然后进行锐化处理完成图像特征点的增强边沿检测，进而将扎把识别转换为直线识别问题。这种方法仍然需要保证扎把的颜色与背景色有较大的差异，但不再需要确定扎把的颜色。由于边沿的色彩差别会导致大量的噪声的存在，以及平滑噪声和边沿检测都需要复杂计算，因此实际过程中难以达到理想的识别速度。

2 熵与图像熵

熵（entropy）指的是体系的混乱的程度，它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。熵由鲁道夫·克劳修斯（Rudolf Clausius）提出，并应用在热力学中。后来，信息论的创始人克劳德·艾尔伍德·香农（Claude Elwood Shannon）第一次将熵的概念引入到信息论中来。他在其著作 《通信的数学理论》中提出了建立在概率统计模型上的信息度量，并把信息定义为 “用来消除不确定性的东西”。

将I（A）＝－logp（A）（其中p（A）为事件A发生的概率）称为事件A的自信息，来度量事件A发生所提供的信息量。把随机事件的N个可能的结果的自信息的平均值：

H＝－sum（p（i）/log（p（i））

称为熵（p1，p2，pn是个事件对应的概率），用作某事件不确定度的量度，是描述事物无序性的参数，熵越大则无序性越强，越不确定，熵为0的事件是确定的。

图像熵把图像的色彩作为随机事件用来确定熵值。使用图像熵表示图像集合的比特平均数，单位为比特/像素，也描述了图像信源的平均信息量。

H＝，其中p（i）代表了色彩度为i的图像的像元在所有像元中所占比例。

3 图像熵在纸币扎把中的应用

以上图像熵可以表示图像色彩分布的聚集特征，却不能反映图像色彩分布的空间特征，为此引入图像的二维熵。

选择图像的邻域色彩均值作为色彩分布的空间特征量，与图像的像素色彩组成特征二元组，记为（i，j），其中i表示像素的色彩值（0＜＝i＜＝255），j表示领域色彩（0＜＝j＜＝255），

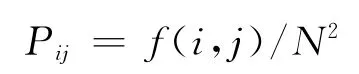
即可反应某像素位置上的色彩值与其周围像素的色彩分布的综合特征，其中f（i，j）为特征二元组（i，j）出现的频数，N为图像的尺度，定义离散的图像二维熵为：

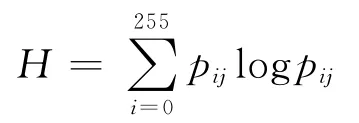
依此构造的图像二维熵可以在反映图像所包含的信息量的前提下，突出反映图像中像素位置的色彩信息和像素邻域内色彩分布的综合特征.

根据扎把的照片可以看到，纸币侧面的各种颜色非常丰富，而其扎把处颜色相对统一，因此通过图像熵的计算就能够区分扎把区域与其它区域的位置。

如将扫描后的图像划分为20×20个小区域，如图1，分别计算每个扎把小区域图像熵。其中，第5行到第16行与第5列到第16列扎把小区域图像熵如表1。

图1 将图形划分为20×20小区域

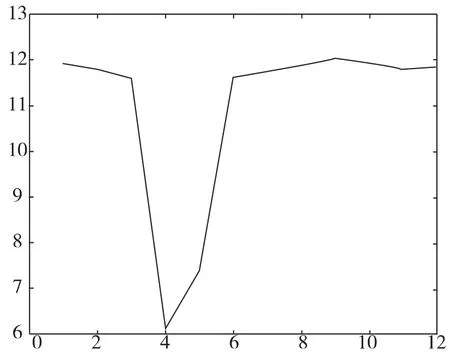
图2 第6行（5～16）列数据的熵值图形

以缩小2倍的列号为x轴，以图像熵值为y轴，做第6行第5列到第16列区域图像熵值二维回归线，如图2，明显看到第8列附近为扎把区。观察第6行与第11行代表图像熵值的各列数据发现，第9行与第10行区域的图像熵值显著性降低，可以容易地实现扎把区域的识别。

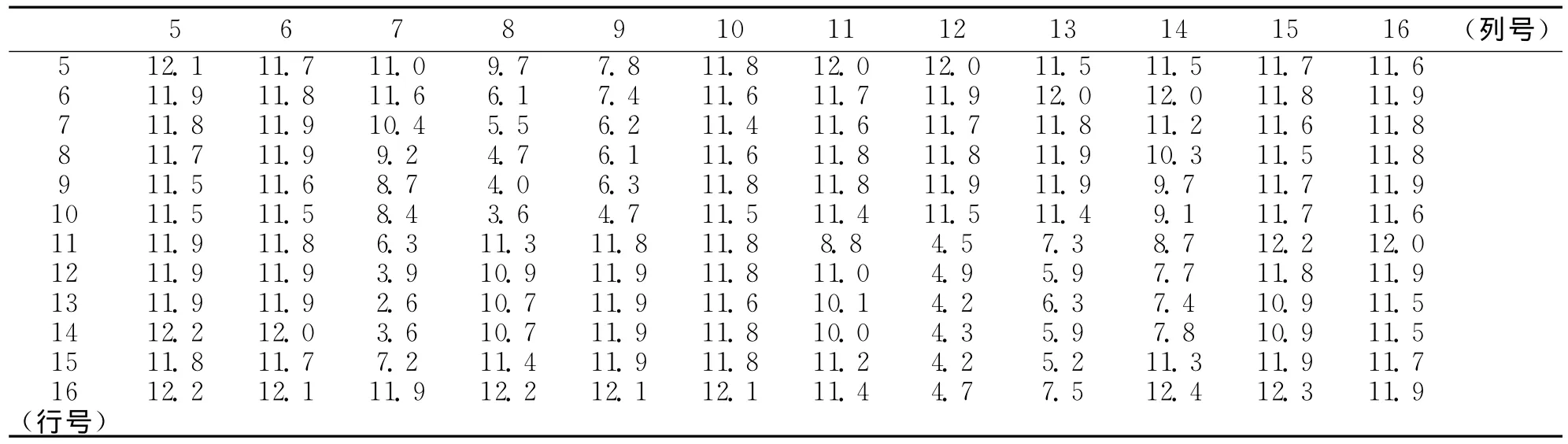
表1 区域图像熵值表

4 结 论

通过图像分块的图像熵计算方式来完成纸币捆中的扎把区域识别不需要指定扎把的颜色，同时其背景色的噪声也不会影响扎把区域的识别，放宽了条件，提高了识别速度，是一种可行的扎把识别方式，具有很好的实用功能。

[1]刘勇奎.计算机图形学的基础算法 [M].北京：科学出版社，2001：1－90.

[2]李伟青，谭建荣，彭群生.基于图段结构的整体识别方法的研究 [J].计算机学报，1998（08）：753－758.

[3]石峰等.信息论基础 [M].武汉：武汉大学出版社，2004：10－76.

[4]董开坤.一种基于图像熵向量的并行图像匹配算法 [J].黑龙江工程学院，2001，（01）：40－43.