标准门洞形过水隧洞正常水深的计算

陈 萍，滕 凯

（1.齐齐哈尔市水政监察大队，黑龙江齐齐哈尔161006；2.齐齐哈尔市水务局，黑龙江齐齐哈尔161006）

普通标准门洞形过水断面是水利水电供排水工程中应用较广泛的断面形式之一。由于该种断面正常水深计算涉及超越方程求解，无法直接获得，而常规解法［1-4］（图表法、试算法）过程繁、精度低，利用微机编程求解又不便实际工作［5］。为了解决了常规算法所存在的问题，有关学者通过大量的分析及研究工作，先后提出了多种简化计算方法［6-10］，具有代表性的研究成果主要为文献［8-10］，文献中提出的方法计算精度较高、公式的表达形式相对好于其他研究成果。但由于这些简化公式均存在2个系数项、1个常数及1个指数项，且数字位数较多，计算公式分段给出，即不便记忆也不够简单。为进一步简化普通标准门洞形过水断面正常水深的计算过程，依据优化拟合原理，以标准剩余差最小为目标函数，经逐次逼近拟合计算，获得了一种可直接完成求解计算的解析表达式，计算过程更加简捷、直观，便于实际应用。

1 正常水深的基本计算公式

根据水力学原理［11］，正常水深的基本计算方程：

式中Q为渠道通过流量（m3/s）；A为过水断面面积（m2）；X为湿周（m）；i为隧洞底坡降；n为隧洞内壁糙率。

1.1 门洞形过水断面水力要素

对于普通标准门洞形过水断面，如图1所示。当正常水深h小于门洞侧墙高度H（对于普通标准门洞形过水断面，H=r）时，可按求解矩形断面正常水深方法完成相关计算；当正常水深h大于门洞侧墙高度H时，过水断面水力要素为：

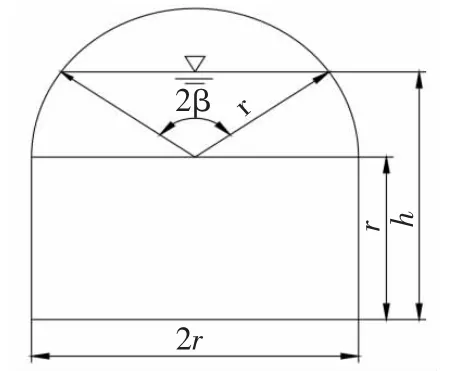
图1 标准门洞形过水隧洞断面示意

式中 r为顶拱圆形半径（m）；β为洞内水面以上圆弧所对圆心角之半（rad）；h为洞内正常水深（m）。

1.2 门洞形过水断面临界流方程

将式（2）至（3）代入式（1），即可获得求解普通标准门洞形过水断面正常水深的基本方程组为：

在式（5）中，设：

式中k为无量纲参数；x为无量纲水深。

经对式（5）方程组变形整理可得计算普通标准门洞形过水断面正常水深：

由式（7）可见，在理论上，x的取值范围为［1，2］，而在实际工程中，为了避免因洞内水位过高产生波状水面引起明满流交替现象，《水工隧洞设计规范》［12］规定，在低流速恒定流情况下，洞内水面线以上的空间不宜小于隧洞断面积的15%，且净空高度不应小于0.4m，由此可以求得x<1.55，本文考虑适当外延，将x的取值范围确定为［1.0，1.8］，相应参数的取值范围为［1.26，2.38］。

2 门洞形过水断面正常水深近似计算

2.1 拟合公式的建立

式（7）为含x的超越方程，无法直接获得解析解。为避免求解超越方程问题，在工程实用参数范围内（即1.0≤x≤1.8，1.26≤k≤2.38），假定函数x=f（k）可以替代式（7）；展绘x～k关系曲线（图略），依据曲线图形关系经数值回归计算，以标准剩余差最小为目标函数［13］，即

式中n为拟合计算的数组数。

经逐次逼近拟合［14］即可获得如下替代函数，即

2.2 拟合公式的精度分析

为比较式（8）与式（7）的拟合精度，在给定的工程实用参数范围内，选取不同的xi代入式（7）即可分别计算出与之相对应的ki，再将ki代入式（8）求得与之相对应的x′i（x′i为近似计算值），并由下式完成拟合相对误差计算，计算结果见表1所示。

式中zi为拟合相对误差（%）；i为拟合计算的第i个数据比较（1、2、3……n）。

由表1 比较可见，在工程实用范围内，即1.0 ≤x ≤1.8，1.26≤k≤2.38，本文式（8）的最大拟合替代相对误差仅为0.685%，完全可以满足实际工程的设计精度要求，而该公式在表达形式上则较文献［8-10］更加简捷、直观。

表1 拟合精度比较

3 应用举例

选文献［10］算例：已知某水库泄洪隧洞的设计泄洪流量为28m3/s，设计横断面为门洞形，顶拱半径2.5m，洞底坡降i=1/2500，洞内壁糙率n=0.014。试计算隧道内的正常水深h值。

根据已知参数即可求得值：

将参数代入式（8）即可求得无量纲水深x：

则可求得正常水深h=3.153m，精确解h=3.156m，公式计算相对误差0.095%。

4 结语

（1）公式的表达形式更加简单直观，常数、系数项及数字位数少，而且计算公式不分段，容易记忆，实际工作仅借助计算器即可方便快捷地完成解算，适于广大基层工程技术人员实际推广应用。可为较复杂断面（如马蹄形及蛋形过水断面）正常水深近似计算公式的建立提供有益的参考。

（2）通过精度比较及算例计算分析表明，虽然公式的计算精度不如文献［8］、［10］高，但最大计算误差也仅为0.685%，完全可以满足实际工程的设计精度要求。

［1］武汉水利电力学院水力学教研室.水力计算手册［K］.北京：水利电力出版社，1983.

［2］华东水利学院.水工设计手册［K］.北京：水利电力出版社，1986.

［3］张生贤，张步南.明渠均匀流临界流代换简捷计算法［A］.中国科学技术协会首届青年学术年会论文集［C］.北京：中国科学技术出版社，1992.

［4］马吉明，梁海波，梁元博.城门洞形及马蹄形过水隧洞的临界水流［J］.清华大学学报：自然科学版，1999，39（11）：32-34.

［5］吴军君，许小健，倪宝艳.城门洞形断面输水隧洞临界水深度的计算方法［J］.城市道路与防洪，2007（9）：12，160-162.

［6］滕凯，李建华，李振宇.标准门洞型过水断面简捷水力计算法［J］.海河水利，1998，92（4）：15-17.

［7］张宽地，吕宏兴，王光谦，等.普通门洞形隧洞正常水深的直接计算方法［J］.农业工程学报，2009，25（11）：8-12.

［8］文辉，李风玲，欧军等.城门洞形断面隧洞正常水深的近似算法［J］.给水排水，33（7）：25-28.

［9］赵延风，刘军，梅淑霞，等.普通城门洞形断面正常水深的近似计算方法［J］.武汉大学学报（工学版），2009，42（6）：773-75.

［10］张宽地，吕宏兴，赵延风.普通城门洞断面正常水深的近似计算式［J］.长江科学院院报，2010，27（2）：34-36.

［11］清华大学水力学教研室.水力学［M］.北京：高等教育出版社，1980.

［12］DL/T5195—2004，水工隧洞设计规范［S］.

［13］王慧文.偏最小二乘回归法及其应用［M］.北京：国防工业出版社，1999.

［14］阎凤文.测量数据处理方法［M］.北京：原子能出版社，1988.