恩格尔定律：理论与检验

王宋涛

（华南师范大学 经济与管理学院，广东 广州 510006）

一、引言

1857年，德国统计学家恩格尔对英、法、德、比等国的有关数据资料进行分析后发现，随着家庭和个人收入增加，收入中用于食品方面的支出比例逐渐减小，这一定律被称为恩格尔定律。由于恩格尔定律的实证可靠性，因此人们使用“食品消费支出占总消费支出比”指标来衡量居民生活水平的变化以及不同国家地区人民富裕程度，该指标被称为“恩格尔系数”。恩格尔系数既能反映收入水平，又能反映消费结构以及基本的消费价格（如食品相对价格），同时又能排除通胀（价格指数）数据有效性的影响。因此用于衡量人们的生活水平，其比居民收入、居民消费指标更有优势，在国际上被广泛应用。虽然国内有不少文献（如马崇明，1994；杭斌和申春兰，2005；姜国刚，2012）[1][2][3]质疑恩格尔系数在我国的适用性，但很多都是基于对恩格尔系数的误读①。由于恩格尔系数的重要性，其一直被我国统计部门作为衡量居民生活水平的一个重要指标，图1反映了随着我国居民收入增长，恩格尔系数也持续下降的事实，从图1可以看出恩格尔定律在我国基本是成立的。

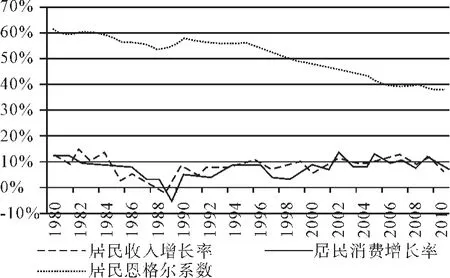
图1 改革开放以来我国居民生活水平变化

然而，恩格尔定律同样受到一些学者的质疑（谢健， 1993；段小兵，1999；张晓霞，2006）[4][5][6]。 由于恩格尔定律只是实证性定律，因此当使用数据进行验证时，数据的来源、处理及计量方法使用上的任一点瑕疵都会影响到结果②。有学者 （王少飞，2002； 张晓霞，2006）[7][8]以个别例子（如认为上海和新疆的居民收入水平差距很大，而恩格尔系数却大体相同）质疑恩格尔定律，国外有学者（Byrne and Capps，1996）[9]则认为恩格尔定律不适合所有的人群。因此，对恩格尔定律进行理论上的推导并进行严谨的实证检验显得尤为重要。当前教科书和相关文献都直接以“必需品”即食品消费的低收入弹性来诠释恩格尔定律，实际上只是同义重复，并没有提供其理论基础。本文对恩格尔定律进行了理论推导，并用我国省际面板数据进行了检验。

二、理论推导

记 cf（≥0）为个体食品消费，ce（≥0）为非食品消费，c=cf+ce为个体总消费；记 cf=f（c）为食品消费函数，则 0≤f（c）≤c，f（0）＝0。

定义f′（c）为“边际食品消费倾向”，即个体增加最后一单位消费所增加的食品消费，若，f″（c）＜0，则称“边际食品消费倾向递减”。

记 y（≥0）为个体的收入，c=g（y）为个体消费函数，一般而言，消费函数为增函数，即 dc/dy=g′（y）＞0。

由于恩格尔定律的可靠性，通过研究食品消费函数的特征，可以发现以下命题：

命题 1：若 f″（c）＜0，即边际食品消费倾向递减，则恩格尔定律成立。

证明：若 f″（c）＜0，则对任意 c0∈（0，c）都有：

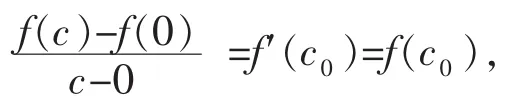
为了进一步获得边际食品消费倾向递减的理论依据，需要借助个体效用函数及个体效用最大化的微观基础。设个体的（CARR型）食品消费效用函数和非食品消费效用函数分别为：

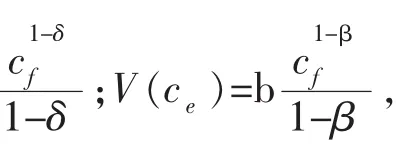
设效用函数具有可加性，即：W（cf，ce）=U（cf）+V（ce），则：

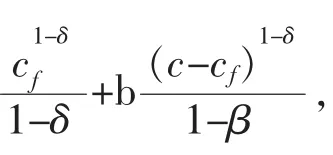
根据马斯洛（Maslow，1943）[10]的需求层次理论，个体的生理需求是最基本的需求，而食物需求则是最首要的生理需求，因此我们假设：

假设1：个体消费先用于食品消费，再用于非食品消费。

实际上，假设 1 意味着∂W/∂cf（0，0）＞0，这比稻田（Inada）条件∂W/∂cf（0，0）=+∞ 还弱，因此假设 1是非常合理的。利用假设1，容易证得以下命题。

命题2：边际食品消费倾向递减。

证明：个体的消费先用于食品消费，再用于其他消费，则在0点食品消费的边际倾向要大于非食品消费的边际倾向，即：

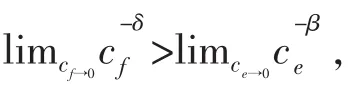
当个体消费c既定，其进行（效用）最大化进行决策时，有∂W/∂cf=0，即：

即：c－δf－b（c－cf）－β=0。 从而：

δ2cf/δc2＜0，即个体边际食品消费倾向递减。

由命题1和命题2可以知道，只要承认马斯洛的需求层次理论，承认食物为人们的第一需求，那么恩格尔定律就是成立的。

三、实证分析

使用1981～2010年我国居民省际面板数据③对边际食品消费倾向递减检验，从而间接论证恩格尔定律的成立；为了保证结论的稳健性，进一步直接检验居民收入与恩格尔系数的关系。由于我国城乡二元结构的特点，我们分别对所有居民、城镇居民和农村居民进行检验。

（一）居民边际食品消费倾向递减的检验——参数δ＞β的检验

根 据式 （1）有 Ln（c－cf）=（1/β）Ln（b）+（δ/β）Ln（cf），因此可设定面板回归模型：

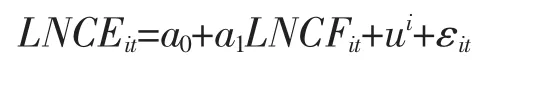
其中下标i表示省份，t表示年份；LNCFit为居民人均食品消费的对数值，LNCEit为居民人均非食品消费的对数值，用人均消费减去人均食品消费再取对数得到，ui表示个体效应，εit为随机误差项。a0+ui为 Ln （b）/β的估计值 （变截距），a1为 δ/β 的估计值。所有数据都使用定基价格指数（1981年为基期）进行了调整，居民总体的数据则分别用城镇居民和农村居民数据按人口比重加权得到④。原始数据来源于全国及各省历年统计年鉴。使用Hausman检验判断使用固定效应模型还是随机效应模型，检验结果支持固定效应模型，估计及检验结果见表1。

从表1可以看出，对所有居民的检验，回归系数在1%显著性水平都通过检验，F统计量在1%水平显著，调整R2为0.9611。从回归系数看，参数a1＞1，这意味着δ＞β，从而边际食品消费倾向递减，根据命题1，恩格尔定律成立。

对于城镇居民和农村居民的检验都有同样的结论，具体不再详述。

（二）我国居民恩格尔定律的直接检验

为了验证上文结论的可靠性，直接对恩格尔系数和居民收入进行检验。根据恩格尔定律的含义，建立对数线性的变截距面板回归模型：

LNENGit为居民恩格尔系数的对数，LNENCit为居民人均收入的对数。居民总体数据使用城镇居民和农村居民数据按照人口比重加权得到，城镇居民使用人均可支配收入指标，农村居民使用人均纯收入指标，收入数据使用居民消费定基价格指数进行调整得到可比值。数据来源同上。Hausman检验支持固定效应模型，检验结果见表1。

可以看出，对所有居民的检验，系数在1%的显著性水平通过检验，F统计量在1%水平显著性，调整R2为0.8974，低于上一个模型，说明上文基于理论推导的计量模型更有解释力。从回归系数值看，居民收入变化对居民恩格尔系数影响的弹性系数为－0.2605，说明恩格尔定律成立。由于我国居民恩格尔系数从1981年的0.593下降到0.384，下降了0.209，人均收入从277.53元上升到489.93元（可比价格），可以计算1981～2010年收入变化对引起的恩格尔系数下降0.245，贡献率为117%⑤。对于城镇居民和农村居民的检验同样表明恩格尔定律成立。

四、结论

本文基于马斯洛层次需求理论，利用效用函数推导出边际食品消费倾向递减的结论，并利用其对恩格尔定律进行了理论推导，从而为恩格尔定律这个“最可靠的实证性规律”增加了理论印记，即只要马斯洛层次需求理论对人类而言是普遍成立的，则恩格尔定律也必然成立。基于1981～2010年我国居民的省际面板数据的实证分析也进一步表明，恩格尔定律对于我国居民而言是成立的。

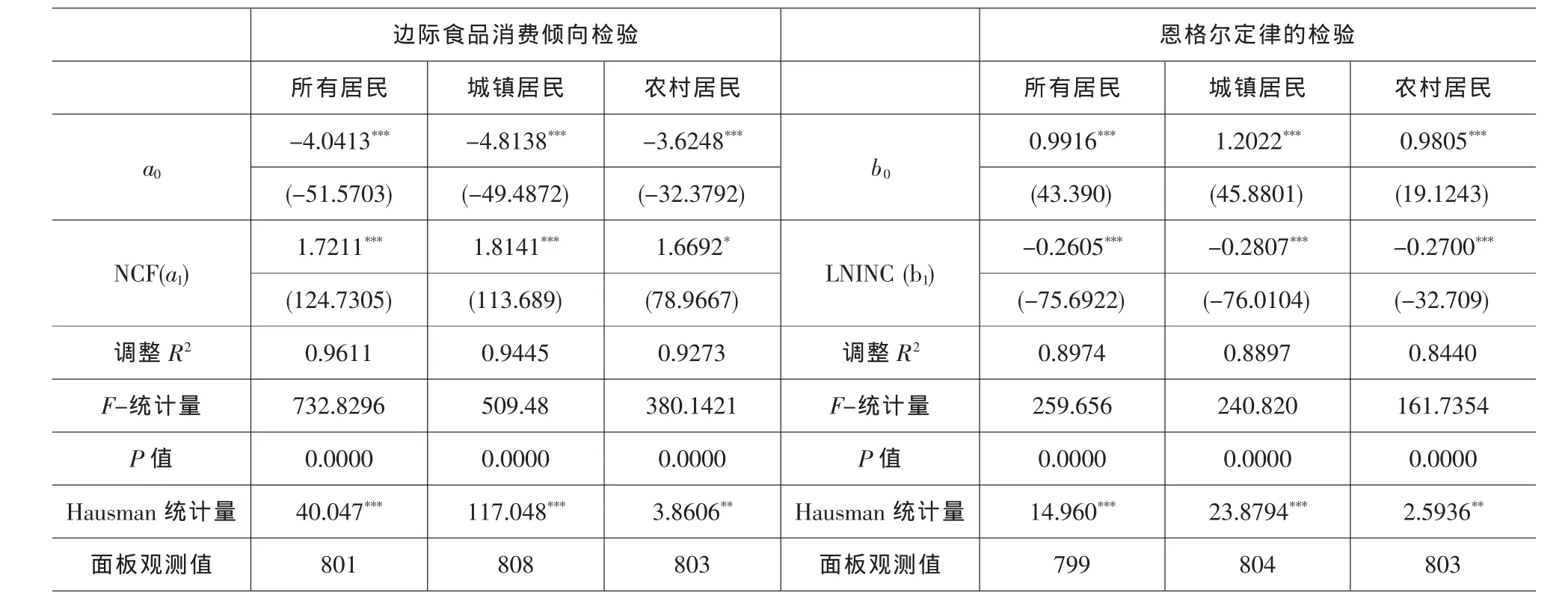
表1 模型检验结果

由于恩格尔定律的可靠性，人们使用恩格尔系数来衡量居民生活水平就具有更强的理论基础，其不但能反映居民收入变化，还可以反映居民的消费水平、消费结构以及价格变化信息，是一个综合的可以用来衡量我国居民生活水平的重要指标。

注释：

① 恩格尔系数在国际是一个通用的衡量居民生活水平的指标，而我国却有不少学者对其在我国的适用性提出了质疑，笔者仔细拜读相关文献后发现很多学者对其存在误读，但关于恩格尔系数的讨论并非本文重点。

② 如名义数据的价格调整、序列数据的自相关性、回归方程控制变量的引入等。

③ 我们使用中国内地的省际面板数据，由于海南、重庆后来才设省（直辖市），数据不全，故剔除；西藏和新疆由于统计数据不全，也剔除，最后共为27个省市的面板数据。由于剔除的省市人口较少，因此对总体结果影响较小。

④ 2000年以前的城镇化数据来源于参考文献[10]根据“五普”数据为基础所做的修补，2000年以后的城镇化率数据来自各省历年统计年鉴。

⑤ 影响恩格尔系数的因素还有食品相对价格、收入分配等因素，由于不是本文重点且数据可得性原因，故没纳入本文模型。

[1]马崇明.试论恩格尔系数在我国的局限性及其解决办法[J].当代财经，1994，（3）.

[2]姜国刚.恩格尔系数失灵的若干影响因素分析[J].华东经济管理，2012，（30).

[3]杭斌，申春兰.恩格尔系数为什么降的这么快[J].统计研究，2005，（1）.

[4]谢健.恩格尔定律的适用性及恩格尔系数的修正[J].统计研究，1993，（1）.

[5]段小兵.平价、分析居民消费水平和富足程度不可盲目照搬恩格尔定律[J]，甘肃金融，1999，（12）.

[6]张晓霞.恩格尔系数与恩格尔定律的正确解读[J].华北金融，2006，（7）.

[7]王少飞.用恩格尔系数衡量居民生活水平的可行性研究[J].统计研究，2002，（6）.

[8]Patrick J.Byrne and Oral Capps， Jr. “Does Engel's Law Extend to Food Away from Home?”Journal of Food Distribution Research.1996，（7）：22-32.

[9]Maslow， A.H. “A theory of human motivation.” Psychological Review， 1943， 50，（4）： 370-396.

[10]周一星，田帅.以“五普”数据为基础对我国分省城市化水平数据修补[J].统计研究，2006，（1）.