双寡头企业产量竞争的均衡质量安全水平研究——以受规制的食品企业为例

费 威

（东北财经大学 数学与数量经济学院，辽宁 大连 116025）

一、引言

随着生活水平的不断提高，消费者对产品质量的要求日益严格，产品质量而非产品价格逐渐成为消费者采购的决定性因素。食品是人类赖以生存和发展的物质基础，食品质量安全关系到人类的健康、社会的稳定和经济的发展。[1]近年来我国食品质量安全事件频发，食品质量安全问题成为社会关心的热点，人们食品消费支出的意愿受到严重影响。为此，我国颁布了《食品安全法》等相关法律法规来规范食品安全，政府相关部门也采取了各种政策措施对食品安全进行监管规制。政府相关部门的规制水平将直接影响到竞争环境中食品企业的生产决策，尤其是产品的质量安全水平决策。

近年来关于在寡头企业数量和价格竞争中引入产品质量分析的国内外研究较多。Choi和Shin[2]在消费者为均匀分布且不考虑质量生产成本情况下，分析了寡占市场中厂商的质量与价格最优决策，认为两家厂商分别会采用高、低不同的质量策略，并且高质量厂商利润大于低质量厂商。Motta[3]研究了不同成本不同竞争方式中均衡质量的选择。Banker等[4]在消费者需求是产品价格和质量水平的线性函数，并且产品成本是质量水平的二次函数条件下，分析了双寡头市场中产品价格和质量两因素的竞争模型，得出了价格和质量都均衡的结论。Aoki[5]研究了Cournot模型和Bertrand模型中不同竞争方式对质量的影响。Wang[6]在成本与质量正相关的假设条件下分析了寡占市场中厂商对质量与价格的决策，认为高质量优势是否存在是由成本随质量上升而增加的速度以及消费者偏好的分布而决定的。Lambertini和Tampieri[7]建立了垂直差异双寡头企业（两个企业非合作）的数量竞争模型，证明了当低质量企业作为领导者时子博弈完美均衡存在。Griva和Vettas[8]研究了在给定产品网络效应下双寡头企业的价格竞争，重点分析了消费者预期不受价格和受价格影响两种情况下生产高低质量产品企业的市场占有率。李丽君等[9]采用委托代理理论的方法探讨了双边道德风险条件下的质量控制策略。高建刚[10]分析了当厂商面对非均匀分布的消费者并且生产成本随质量变动时，厂商在利润最大化假设下的质量与价格决策。谢科范等[11]根据质量成本曲线的特殊性以及质量的时效性建立了质量竞争博弈模型，分析了质量竞争机理以及质量竞争过程中的企业风险。杨树等[12]分别利用Cournot模型和Bertrand模型分析和比较了数量竞争和价格竞争下的均衡质量，结果表明不同的市场条件会导致不同的比较结果。鲁其辉和朱道立[13]研究了二层供应链模型中供应链在产品质量和价格两个方面进行竞争时无协调、混合和协调的三个情景，分析表明协调策略对于每条供应链都是占优策略，并且质量成本优势越大的供应链，采用协调策略后收益越大。吴小节等[14]研究了企业将产品质量作为维持顾客忠诚度的双寡头企业竞争策略，认为产品质量是一个重要的竞争性变量，企业可以通过产品质量等方式形成商誉。龚日朝和刘玲[15]在考虑商品价格和质量水平的需求市场中，分析了双寡头企业的价格和质量竞争博弈，认为纳什均衡状态下两个企业必须采取一定的差异化策略。

现有研究都是针对一般性产品而言的，对于质量安全水平直接影响消费者身体健康的食品并没有具体研究。同时，结合我国当前食品安全监管的实际情况，消费者对食品质量安全的偏好或支付意愿直接受到政府相关部门监管规制水平的影响。在具有质量安全水平差异的双寡头食品生产企业竞争模型中，若考虑规制水平，那么其是否会影响企业的均衡质量水平及其相互关系？回答这一问题将为政府相关部门监管食品企业提供一定参考，也为企业实行质量安全生产决策提供一定依据。因此，本文在文献[8]基本模型设定基础上，引入政府相关规制水平这一变量，并对模型的相关假设进行了扩展变形，分析了生产高、低质量安全水平产品的双寡头企业分别在古诺 （Cournot）和斯塔克尔伯格（Stackelberg）博弈模型中的均衡质量水平及其相互关系。此外，本文的分析是在完全信息的假设下进行的，把同时生产高、低质量安全水平的两个企业之间进行的博弈分为了两个阶段：第一阶段，两个企业依据各自利润选择产品的质量安全水平；第二阶段，两个企业的决策变量是产品数量（即产量）。

二、基本模型分析

（一）假设条件和变量符号

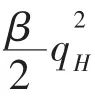
消费者对产品质量安全的支付意愿用θ表示，并假设消费者的支付意愿θ是服从0－1区间均匀分布的随机变量，即 θU［0,1］，0≤θ≤1。 因为不同消费者对产品质量安全的支付意愿是不同的，所以假设它是随机变量，同时为便于分析并不失一般性，假设其服从均匀分布。考虑到消费者对政府相关部门规制水平r的认知和信任程度这一因素，令α表示消费者对规制水平的认知和信任程度，其中0≤α≤1，当α=0时表示消费者对政府相关部门规制完全不认可和不信任，当α=1时表示消费者对政府相关部门规制完全认可和信任。在实际中，消费者对政府相关部门实行的规制措施越信任，就越会增强其对产品质量安全的实际支付意愿，因此令消费者对产品质量安全的实际支付意愿为θc=θ+αr。假设消费者最多购买1个单位产品，并且消费者是风险中性的，则可令消费者的效用函数是其消费产品所得净收益的线性函数，即 U=θcqi－pi。

整理式（1）有

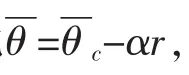
根据θ服从密度为1的均匀分布，可得市场对高质量安全水平产品的需求量为

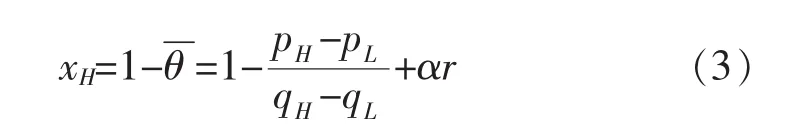
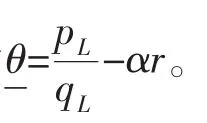
相应地可得市场对低质量安全水平产品的需求量为

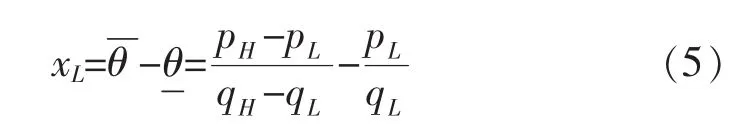
联立式（3）和（5）可得企业H和L的市场需求函数如下

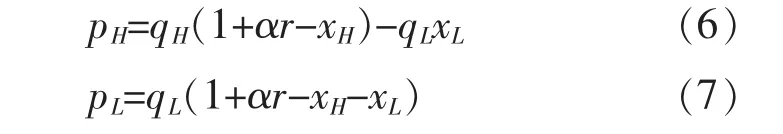
企业H和L的利润分别为

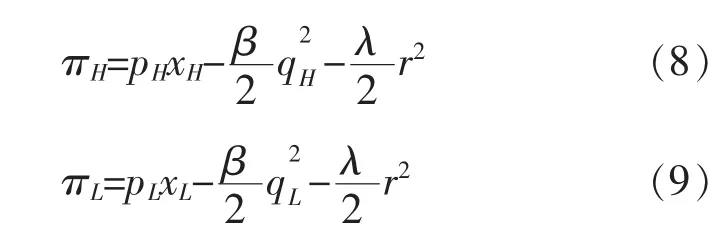
（二）古诺模型中的均衡质量安全水平分析

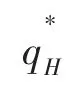
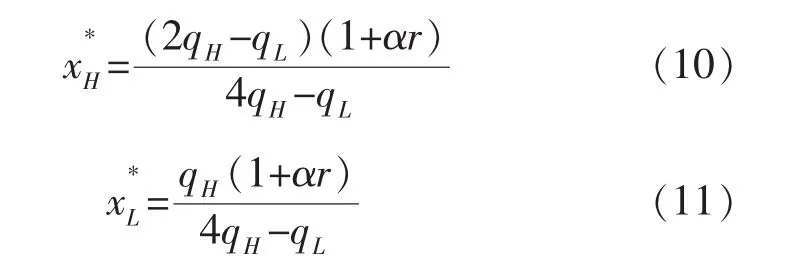
将式（10）和（11）代入式（8）和（9）可得

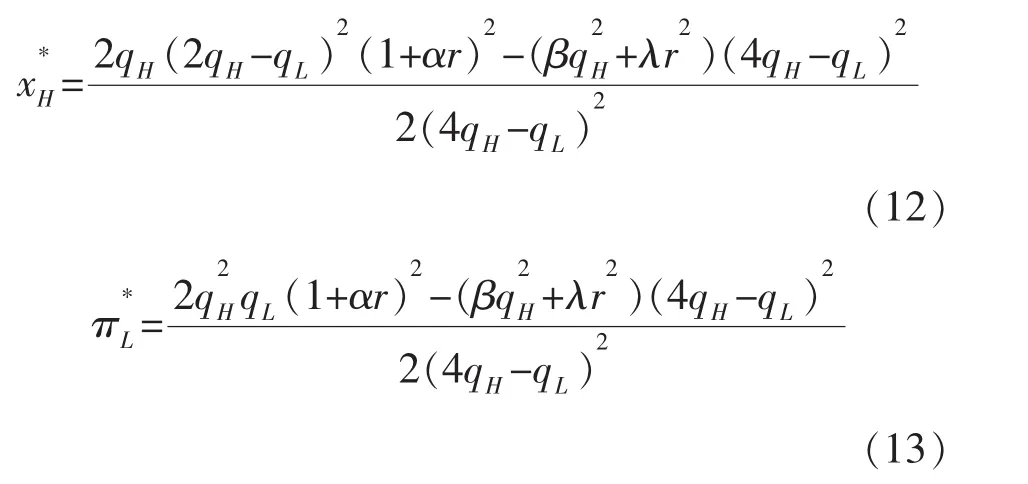
因此，对式（12）中qH和qL求二阶偏导数可得

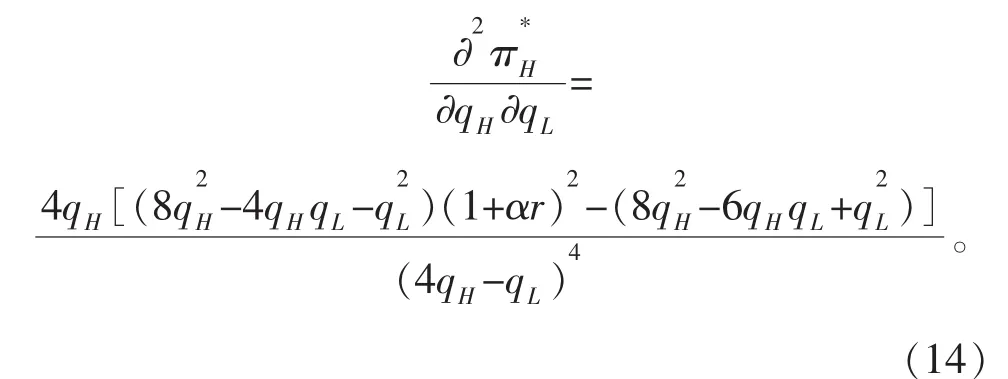
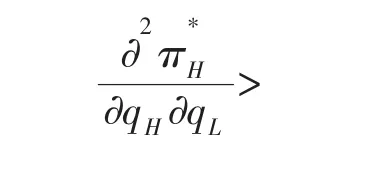
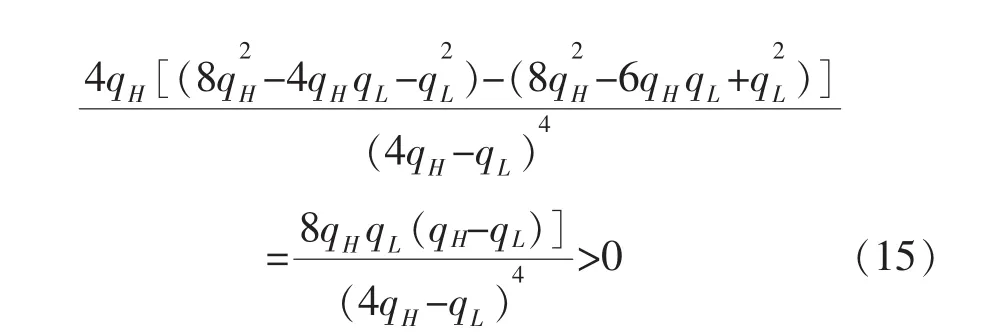
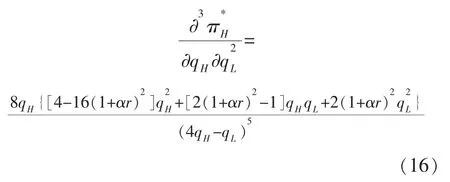
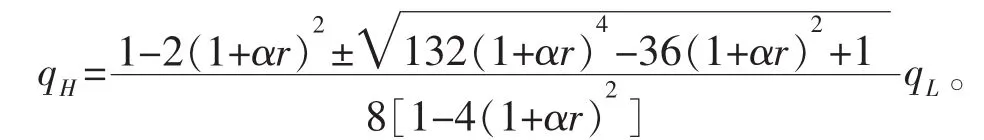
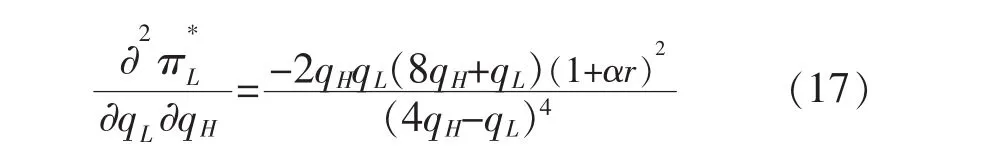
根据式（17）进一步对qH求导可得

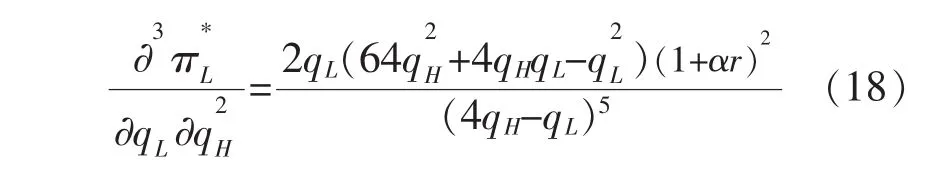
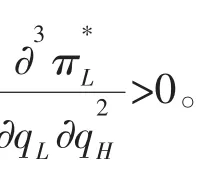
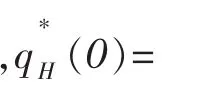
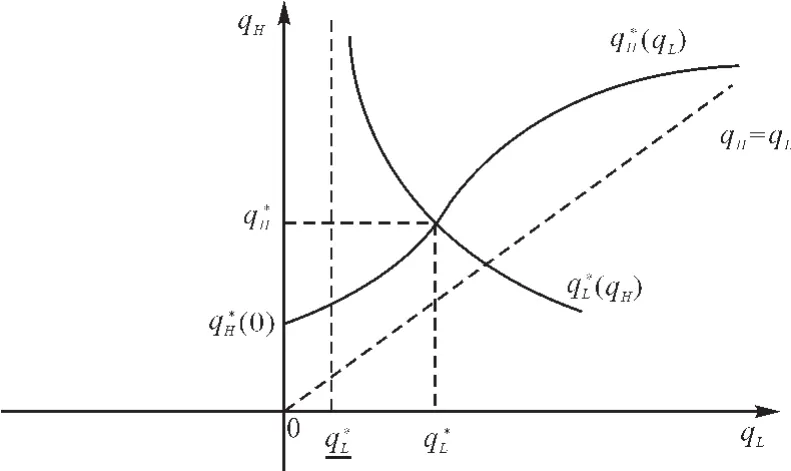
图1 古诺模型中两个企业的均衡质量安全水平

因此，在古诺模型中尽管两个企业没有行动先后而是同时按照各自利润最大化决定最优产量，进而最终确定各自的最优质量安全水平，但高质量安全水平企业的最优质量安全水平仍然受到低质量安全水平企业的质量安全水平的正向影响，即若低质量安全水平企业提高其最优质量安全水平，高质量安全企业也会相应提高其自身的质量安全水平。这主要是由于消费者对产品质量安全水平的偏好决定了两个企业产品的市场占有量。因此，低质量安全企业若提高其产品质量安全水平会刺激高质量安全企业进一步提高其产品质量安全水平，以确保一定的市场产品占有率。同时，低质量安全水平企业的最优质量安全水平受到高质量安全企业的质量安全水平的反向影响，即若高质量安全水平企业提高其最优质量安全水平，低质量安全企业会降低其自身的质量安全水平。这主要是由于两个企业本身存在一定的质量安全水平差距，而高质量安全水平企业进一步提高其产品质量安全水平，则进一步拉大了与低质量安全水平企业的产品质量安全差距，抢占了更大的市场份额，这种效应会大于低质量安全水平企业提高自身产品质量安全而带来的市场占有率的小幅增加，并且低质量安全水平企业提高质量安全水平还要付出相应生产成本，因此它会选择降低质量安全水平以节省一定成本补偿部分利润损失。

三、斯塔克尔伯格模型中均衡质量安全水平分析

（一）企业H作为领导者的均衡质量安全水平分析

在高质量安全水平企业H作为产量领导者的斯塔克尔伯格模型中，企业H根据低质量安全水平企业L的产量反应函数xL（xH）决定自身利润最大化的最优产量，低质量安全水平企业L的产量则由xL（）给定，最后两个企业分别依据各自利润最大化决定均衡的质量安全水平和

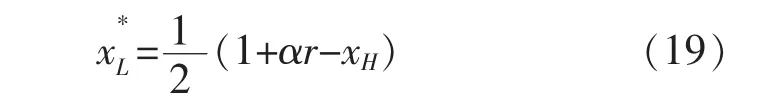
将式（19）代入式（6）和（8），由可得

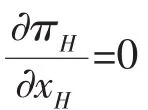
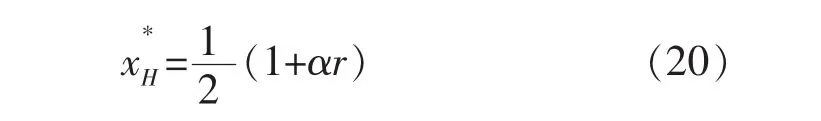
将式（20）代入（19）有

将式（20）和（21）代入 πL和 πH表达式，整理可得

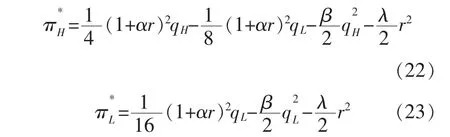
根据上述分析可得：在以生产高质量安全水平产品的企业H为产量领导者的斯塔克尔伯格模型中，当两个企业按照各自利润最大化决定最优质量安全水平时，存在两个企业的均衡质量安全水平；在均衡点处，企业H的质量安全水平是企业L的4倍，企业H的价格是企业L的7倍，企业H的产量是企业L的2倍，同时领导者企业H的利润高于企业L；当其他条件不变时，两个企业的最优质量安全水平、价格和产量都是政府相关部门规制水平的增函数。

（二）企业L作为领导者的均衡质量安全水平分析

在低质量安全水平企业L作为产量领导者的斯塔克尔伯格模型中，企业L根据高质量安全水平企业H的产量反应函数xH（xL）决定自身利润最大化的最优产量，高质量安全水平企业H的产量则由xH（）给定，最后两个企业分别依据各自利润最大化决定均衡的质量安全水平和

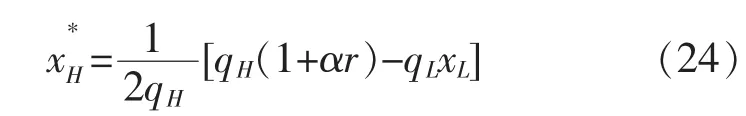
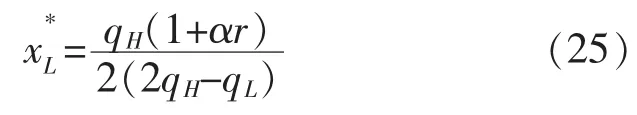
将式（25）代入（24）有

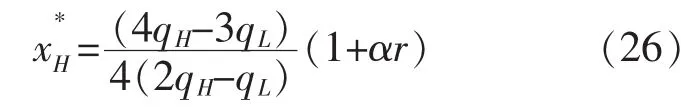
将式（25）和（26）代入πL和πH表达式，整理可得

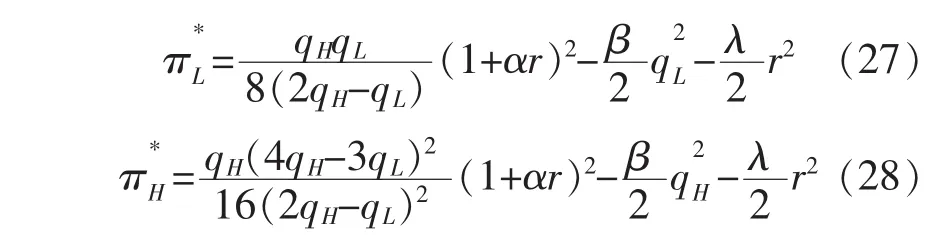
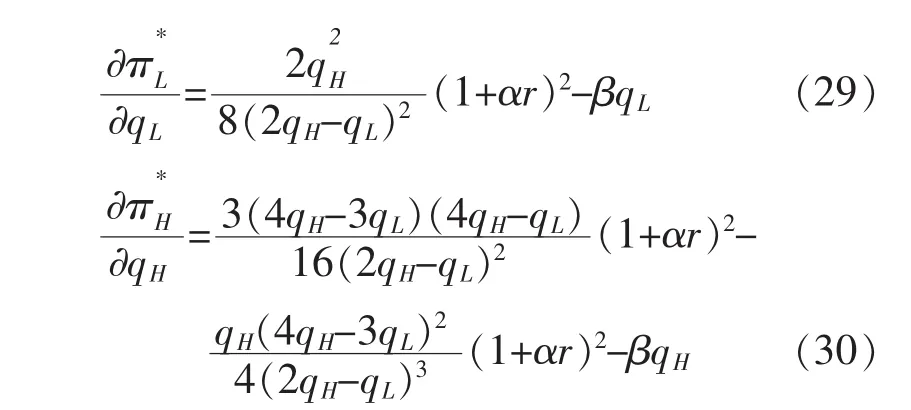
满足式（29）和（30）分别为企业 L和H的最优质量安全水平和。因为表达式较为复杂，在此没有给出具体的显性表达式。与2.2节类似，有

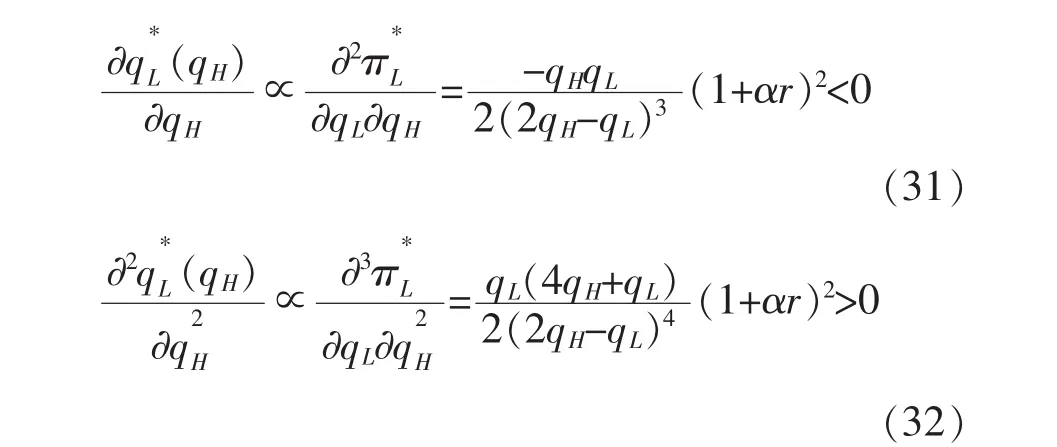
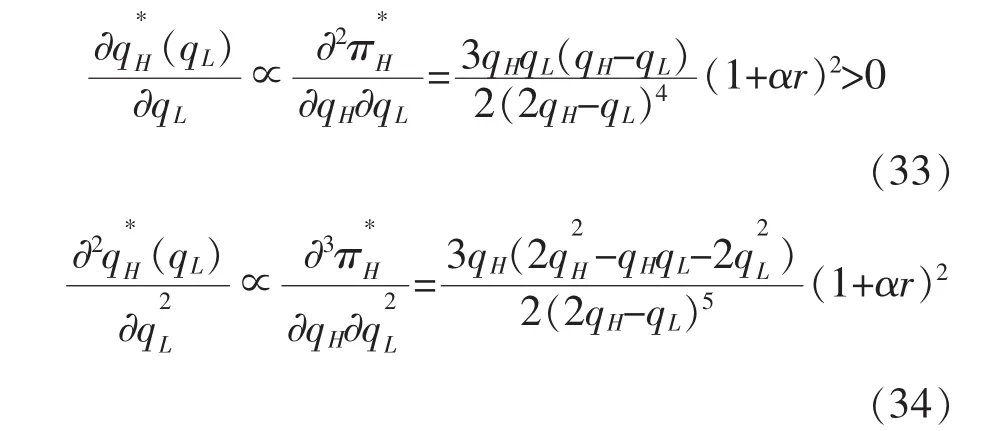
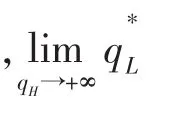
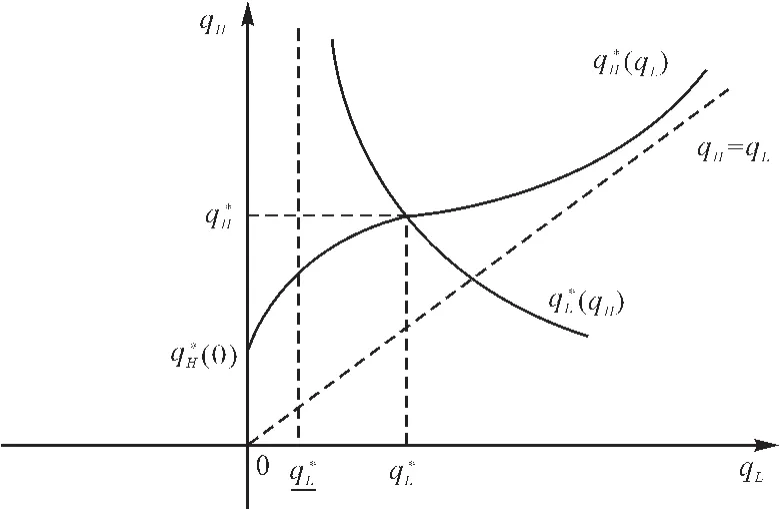
图2 低质量企业为领导者的两个企业最优质量安全水平反应函数

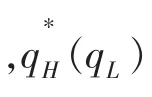
四、结论

本文分别利用古诺模型和斯塔克尔伯格模型对双寡头食品企业产量竞争中的均衡质量安全水平进行了分析，得出以下主要结论：

首先，在古诺模型中，当生产高、低质量安全水平的企业按照各自利润最大化决定最优质量安全水平时，生产高质量安全水平企业的最优质量安全水平是低质量安全水平的单调增函数，并且当其最优质量安全水平较低时是低质量安全水平的凸函数，当其最优质量安全水平较高时是低质量安全水平的凹函数；生产低质量安全水平企业的最优质量安全水平是高质量安全水平的单调减和凸函数；并且两个企业都可以实现最优质量安全水平，即存在均衡点，在这一点处对应两个企业的均衡质量安全水平。

其次，在斯塔克尔伯格模型中，当生产高、低质量安全水平的企业分别作为产量领导者时，会得出不同的均衡质量安全水平结论。以生产高质量安全水平产品的企业为产量领导者时，存在两个企业的均衡质量安全水平，并且在均衡点处，作为领导者的企业生产的产品质量安全水平是追随者企业的4倍，其价格是追随者企业的7倍，其产量是追随者企业的2倍，同时领导者企业的利润远高于追随者企业。而且当其他条件不变时，两个企业的均衡质量安全水平、价格和产量都随着政府相关部门规制水平的提高而上升。以生产低质量安全水平产品的企业为产量领导者时，生产高质量安全水平企业的最优质量安全水平是低质量安全水平的单调增函数，并且当其最优质量安全水平较低时是低质量安全水平的凹函数，当其最优质量安全水平较高时是低质量安全水平的凸函数；生产低质量安全水平企业的最优质量安全水平是高质量安全水平的单调减和凸函数；并且两个企业都可以实现最优质量安全水平，即存在均衡点，在这一点处对应两个企业的均衡质量安全水平。

最后，比较两类模型中的均衡质量安全水平可见，古诺模型中高、低质量安全水平企业的均衡质量安全水平结论，与在斯塔克尔伯格模型中低质量安全水平企业作为产量领导者的均衡质量安全水平结论相似，其中只有一点不同，即在古诺模型中高质量安全水平企业的最优质量安全水平是低质量安全水平企业的质量安全水平的先凸后凹函数，而在低质量安全水平企业作为产量领导者的斯塔克尔伯格模型中却是低质量安全水平企业的质量安全水平的先凹后凸函数。这说明双寡头企业在产量竞争中采取的博弈方式不同将不仅影响其利润水平，还将直接影响它们均衡质量安全水平及其最优质量安全水平之间的关系。因此，在当前产品质量安全水平日益受到消费者关注和重视的情况下，双寡头企业在实际竞争中更应考虑竞争方式对它们产品质量安全水平的影响，进而作出与质量安全水平相关的生产决策。

[1]龙一平，徐宏伟.食品安全与政府管制[J].湖北经济学院学报（人文社会科学版），2006，（12）：93－95.

[2]Choi C.，H Shin.A Comment on a Model of Vertical Product Differentiation[J].Journal of Industrial Economics，1992，（2）：229－232.

[3]Motta M.Endogenous Quality Choice：Price vs Quantity Competition[J].The Journal of Industrial Economics，1993，（2）：113－131.

[4]Banker R.D.，Khosla L.，Sinha K.K.Quality and Competition[J].Management Science，1998，（9）：1179-1192.

[5]Aoki R.Effect of Credible Quality Investment with Bertrand and Cournot Competition [J].Economic Theory， 2003，（2-3）：653-672.

[6]Wang H.A Note on the High-quality Advantage in Vertical Differentiation Models[J].Bulletin of Economic Research， 2003， （1）：91-99.

[7]Lambertini L.，Tampieri A.Low-quality Leadership in a Vertically Differentiated Duopoly with Cournot Competition[J].Economics Letters， 2012，（3）：396-398.

[8]Griva K.，Vettas N.Price Competition in a Differentiated Products Duopoly under Network Effects [J].Information Economics and Policy， 2012， （1）： 85-97.

[9]李丽君，黄小原，庄新田.双边道德风险条件下供应链的质量控制策略[J].管理科学学报，2004，（1）：42-47.

[10]高建刚.双寡头模型下的产品质量竞争与厂商决策[J].山西财经大学学报，2006，（2）：8-13.

[11]谢科范，陈刚，彭华涛，施伟.双寡头企业质量竞争博弈分析[J].武汉理工大学学报 （信息与管理工程版），2007，（10）：105-108.

[12]杨树，梁樑，熊立.Cournot和Bertrand竞争下均衡质量的比较[J].系统管理学报，2008，（1）：104-109.

[13]鲁其辉，朱道立.质量与价格竞争供应链的均衡与协调策略研究[J].管理科学学报，2009，（3）：56-64.

[14]吴小节，汪秀琼，龙志和，宋铁波.基于商誉的双寡头企业广告与产品质量竞争策略[J].管理学报，2010，（8）：1152-1158.

[15]龚日朝，刘玲.企业差异化战略对价格和质量竞争博弈均衡解的影响研究[J].经济评论，2011，（1）：23-30.