基于三通道不可分对称小波的多聚焦图像融合

黄倩文,刘斌,李庄

(1.湖北大学数学与计算机科学学院,湖北 武汉 430062;2.武汉科技大学信息科学与工程学院,湖北 武汉 430081)

0 引言

随着传感器技术的迅猛发展,单一传感器获取的信息量已无法满足实际需要,对多源数据的处理使得数据融合技术快速发展起来.图像融合是数据融合中的一个非常重要的分支,它综合了信号处理、图像处理、人工智能等现代高新技术.Pohl等定义图像融合为通过一种特定的算法将两幅或多幅图像合成为一幅新图像[1].多聚焦图像融合是图像融合中的一种,由于光学成像系统聚焦范围的有限,使其无法获得场景中的所有目标都成清晰的图像,因此需要对同一场景不同目标进行多次成像,然后通过图像融合得到一幅场景中目标都成像清晰的融合图像.

根据近年来国内外图像融合领域的最新研究成果,基于多分辨率分析的多聚焦图像融合算法的方法主要有金字塔变换的融合和小波变换的融合算法[2-4],而金字塔分解结构中不同分辨率细节彼此相关,算法稳定性差.基于小波分解的融合方法注意到了图像的方向性,但是传统的基于张量积小波分解的图像融合方法只强调了水平方向和垂直方向,而忽略了其他方向.为了克服小波分解方向性的不足,产生了多种新的图像融合方法.目前主要有基于Curvelet的融合方法[5]、基于Contourlet变换的融合[6]和基于复小波变换等融合方法.

基于张量积小波变换的方法在图像分解时采用下二抽样,因此不具备平移不变性,并使得结果图像存在块效应和人工痕迹.除haar小波外,张量积小波都不能同时具有紧支撑性、正交性和对称性,但haar小波过于简单,处理图像效果不理想.其他小波,如Daubechies系列小波的不对称性会使图像发生偏移,双正交小波不具备正交性,在图像分解和重构时会产生信息的冗余.在非张量积小波理论框架下发展起来的不可分小波是一类新的小波,它不仅强调图像的多方向性,而且能很好地满足三性,即紧支撑、正交性和对称性,同时,此种小波能较好地提升融合图像的空间分辨率.目前,不可分小波有二通道、三通道、四通道小波,三通道不可分小波相对于同类小波具有更好的融合性能[7-9].

本文中选用二维三通道不可分对称的小波滤波器组,对多聚焦图像进行处理.相对于传统的只对小波分解后的低频部分进行处理,而对多个高频子带仅采用加权平均、绝对值取大或直接取代的方法,本文中对高频部分采用基于区域锐度特性的算子进行处理,实验分两组进行,分别对有参考图像和无参考图像的多聚焦图像对进行仿真实验,并用平均梯度、相关系数和空间频率等对融合结果进行客观评价.实验结果表明,在主观视觉效果和客观评价指标上该算法取得优于传统方法的融合效果.

1 二维三通道不可分小波滤波器组的构造

根据小波变换与多尺度分析理论,当抽样矩阵为M=[2,-1;1,1]时,M的行列式的值为3,故有3个通道,1个低通通道和2个高通通道,相应地有1个尺度函数和2个小波函数,从而对应地有1个低通和2个高通滤波器,若此时的尺度函数和小波函数都不能分解为一维的尺度函数和一维的小波函数的张量积,则称此小波为不可分小波.图1和图2给出了小波的两层分解及重构,实际上还可以进行多层小波分解与重构.

图1 图像的三通道NWF分解

图2 图像的三通道NWF重构

目前,三通道不可分小波已经在多光谱图像的融合及红外图像与可见光图像的融合处理中取得了较好的融合效果,但是将三通道不可分小波用于多聚焦图像融合的方法还不多见.根据高维小波的构造理论,利用本文中提出的基于抽样矩阵M=[2,-1;1,1]的二维三通道小波滤波器组的构造方法构造三维三通道不可分小波滤波器.

(1)

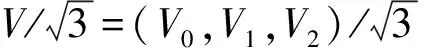
为构造三通道不可分小波的滤波器组,取K=1,构造正交对称矩阵U1和正交矩阵V,根据其正交性可求得矩阵中各个位置的参数值,下面给出一组U1和V的矩阵构造：

(2)

由(1)式可知,给出的U1和V的矩阵不同,产生的滤波器组也是不同的.上面给出的只是滤波器组的一种取值.则相应的滤波器组的时域形式如下：

(3)

显然,此滤波器组是对称的,也是不可分的.

2 改进的多聚焦图像融合规则

融合结果图像效果的好坏主要取决于融合算法和融合规则的选取是否得当.目前,基于不可分小波的融合规则分为绝对值取大选择法、加权平均法和取代法.这些传统的基于单像素点的方法有一定的适用情况,而基于区域特性的融合规则已成为现阶段的研究热点.本文中的算法也是在此基础上提出的.

2.1低频子带融合规则根据小波变换理论,小波分解后的低频波段表征图像的近似部分,经过不同传感器得到的同一场景的图像,其低频近似部分的系数差别不大.而多聚焦图像融合的目的是获取信息丰富的全聚焦图像,所以对低频部分的处理应主要考虑如何获取较丰富的图像信息.基于区域能量的融合规则能较好地保持源图像的丰富信息,故选取加权区域能量规则对低子带进行处理,具体算法如下.

(4)

(5)

(6)

2.2高频子带融合规则图像的高频子带表征图像的细节信息,高频波段的系数在零值左右波动,系数绝对值越大,表示该处亮度变化越剧烈,即可能包含图像的重要信息.并且,经过不同传感器得到的同一场景的图像,高频细节部分存在显著的差异.所以高频部分融合规则的选取对融合结果图像的清晰度有着至关重要的影响.平均梯度能较好地反映图像中的微小差异,因此,提出基于区域锐度的融合方法.具体算法如下：

(7)

(8)

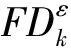
(9)

2.3主要的评价指标采用以下一些评价指标来评价融合图像的质量,在下列式中,F表示融合后的图像,M和N分别表示图像的行数和列数.

2.3.1 空间频率(SF)

(10)

(11)

(12)

空间频率反映了一幅图像空间域的总体活跃程度.空间频率越大,图像融合效果越好.

2.3.2 相关系数(CC)

(13)

2.3.3 标准差(SD)

(14)

式中标准差是由均值间接求得的,图像的标准差反映了图形的像素的分布情况.在某种程度上,标准差可以用来评价图像反差的大小.若标准差大,则图像的对比度大,图像包含更多的信息;若标准差小;图像反差小,则对比度小.

(15)

PSNR反映了融合图像与标准图像对应位置上的像素的差异.峰值信噪比的值越大,表示融合后的图像越接近标准图像,融合后图像效果越好.

2.3.5 信息熵(En) 图像的熵可以反映融合图像信息量的多少.图像信息熵的定义为

(16)

式中,L为图像总的灰度级数;Pi为灰度值为i的像素数Ni与图像像素N之比.

3 实验结果及分析

为了验证提出的方法的可行性,笔者进行了大量实验,这里展示两组实验结果.第一组是有参考图像的多聚焦图像book,图3(a)为参考图像,图3(b)为左聚焦图像,图3(c)为右聚焦图像,源图像大小为9 601 280;考虑到实际中无参考图像的情况更加普遍,另一组是无参考图像的pepsi图像,源图像大小为512 512,图4(a)是左聚焦图像,图4(b)是右聚焦图像.

为了验证算法的有效性,将本文中算法与DWT方法进行对比仿真实验.实验采用本文中构造的二维三通道不可分小波和db2小波分别对图像进行分解和重构,分解层数为3.全部仿真实验均在MATLAb7.1编程环境中实现.图3(d)、(e)和图4(c)、(d)分别为本文中算法的融合结果和DWT-db2的融合结果.从融合结果图像看出,本文中算法在图像清晰度和对比度方面都优于基于DWT算法.

图3 第一组有参考图像的多聚焦图像融合结果

图4 第二组无参考图像的多聚焦图像融合结果

表1和表2分别为第一组和第二组多聚焦图像融合结果的几个客观评价指标的比较.为了凸显提出的算法在不同方面的融合效果,两组实验分别部分采用了不同的评价方法.从表1和表2可以看出,在PSNR、En、CC、SF、SD这几个方面,本文中提出的图像融合算法都优于DWT算法.

表1第一组多聚焦图像的客观性能比较

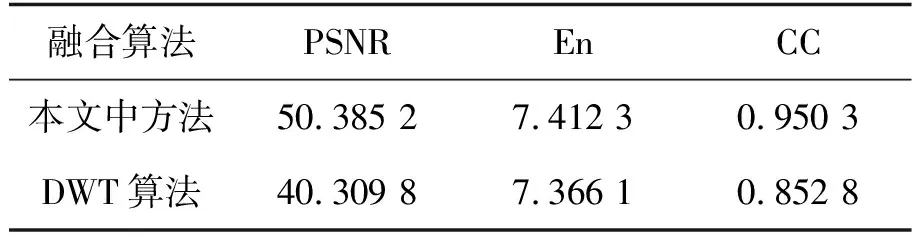
融合算法PSNREnCC本文中方法50.385 27.412 3 0.950 3DWT算法40.309 87.366 1 0.852 8

表2 第二组多聚焦图像的客观性能比较

4 结语

提出一种基于三通道不可分小波多聚焦图像融合新算法.针对源图像经不可分小波分解后在不同尺度与方向下的低频系数和高频系数,分别讨论低频系数和高频系数的融合规则.低频子带反映了图像的轮廓,集中了图像的大部分能量,而且低频系数之间存在区域相关性,因此提出区域能量融合规则来确定低频融合系数;在不同尺度与方向下的高频系数反映了图像的细节和边缘,并且经过不同传感器得到的同一场景的图像,高频细节部分存在显著的差异,因此提出基于区域平均锐度的融合规则来确定高频系数.实验结果表明,在主观视觉效果与客观评价指标上,本文中方法优于传统的方法,并且取得了更好的融合效果.

[1] POHL C, Van Genderen J L. Multisensor image fusion in remote sensing:concepts,methods and applications[J].International Journal of Remote Sensing,1998,19(5):823-854.

[2] 陈浩,王延杰.基于拉普拉斯金字塔变换的图像融合算法研究[J].激光与红外,2009,39(4):339-442.

[3] 李建林,余建成,孙胜利.基于梯度金字塔图像融合的研究[J].科学技术与工程,2007,7(22):5818-5822.

[4] 赵天昀,徐振强,李正文.基于小波变换的多聚焦图像融合方法[J].计算机应用,2004,6(24):157-159.

[5] 吴芳平,狄红卫.一种基于Curvelet变换的图像融合新算法[J].光电子激光,2008,19(7):953-957.

[6] Cunha Arthur L, Zhou Jianping, Do M N. The nonsubsampled contourlet transform:theory,design,and applications[J].IEEE Trans on Image Processing,2006,15(10):3089-3101.

[7] 刘斌,彭嘉雄.基于二通道不可分加性小波的多光谱图像融合[J].光学学报,2007,8(27):1419-1424.

[8] 刘斌,彭嘉雄.基于四通道不可分加性小波的多光谱图像融合[J].计算机学报,2009,2(32):350-356.

[9] 刘斌,刘维杰,彭嘉雄.基于三通道不可分对称小波的红外与可见光图像融合[J].红外与激光,20011,5(40):974-979.

[10] Chen Q H, Micchell C A, Peng S L, et al. Multivariate filter banks having matrix factorizations[J].SIAM Journal on Matrix Analysis and Applications,2003,25(20):517-531.