不确定性推理方法在油田应急指挥系统的应用

康朝海 (东北石油大学电气信息工程学院，黑龙江 大庆 163318)

滕 飞 (大庆油田有限责任公司第三采油厂，黑龙江 大庆 163113)

张东旭 (天津通卡公用网络系统有限公司，天津 300384)

公丽颖 (东北石油大学电气信息工程学院，黑龙江 大庆 163318)

不确定性推理方法在油田应急指挥系统的应用

康朝海 (东北石油大学电气信息工程学院，黑龙江 大庆 163318)

滕 飞 (大庆油田有限责任公司第三采油厂，黑龙江 大庆 163113)

张东旭 (天津通卡公用网络系统有限公司，天津 300384)

公丽颖 (东北石油大学电气信息工程学院，黑龙江 大庆 163318)

在比较几种不确定推理方法的基础上，并针对油田生产中，事故发生时所表征的现象证据往往不完善，且具有一定的模糊性这一问题，提出了一种带有比较因子的加权不确定性推理方法。油田实例分析说明，该方法既能保持推理精度又能加快推理的速度。

不确定性推理；可信度模型；加权因子；比较因子

推理就是从已知事实出发，运用已掌握的知识推导出其中蕴涵的事实性结论和归纳出某些新结论的过程。常规的推理一般是针对确定性知识的，但在油田生产中，事故发生时所表征的现象证据往往是不完善的，且具有一定的模糊性。目前，不确定性推理方法可以分为2大类：控制方法和模型方法[1]。控制方法的特点是通过识别领域中引起不确定性的某些特征及相应的控制策略来限制或减少不确定性系统产生的影响，这类方法目前没有处理不确定性的统一模型，其效果大大依赖于控制策略。模型方法的特点是把不确定性的证据和不确定性的知识与某种度量标准对应起来，并给出更新结论不确定性的合适的算法，从而构成相应的不确定性推理模型。模型方法又可分为数值方法和非数值方法。数值方法按照所依据的理论不同又分为基于概率的方法和模糊推理方法。

在数值推理方法中，由于概率论有着完善的理论，同时还为不确定性的合成与传递提供了现成的公式，因而成为度量不确定性的重要手段。但虽然纯概率方法有着严密的理论依据，它却需要给出事件的先验概率和条件概率，而这些数据又是不易获得的。为此，人们经过多年研究，在概率论的基础上，发展了一些新的处理不确定性的方法：主观Bayes方法、证据理论方法和可信度方法[2-3]。笔者在对几种常用的不确定性推理方法比较的基础上，提出了带有加权因子的不确定性推理模型(CCWR)。

1 几种不确定方法的比较

主观Bayes方法又称主观概率论，是一种基于概率逻辑的方法。主观Bayes方法的基本思想是针对不确定推理，将所有的知识规则连接成一个有向图，图中的各节点代表假设结论，弧代表规则，并引入用来度量规则成立的充分性和必要性的2个数值，通过与每一条弧相关联，建立起一个有向的推理网络。推理过程从图的端点(原始证据)出发，逐级计算概率最后推导出结论的概率[4-6]。

证据理论又称D-S理论，该理论满足比概率论弱的公理，能区分“不确定”与“不知道”的差异，并能处理由“不知道”引起的不确定性。在D-S理论中，知识的不确定性是通过一个集合形式的“可信度因子”来表示，而证据和结论的不确定性度量则采用信任函数和似然函数来表示。然而信任函数和似然函数是以概率分配函数为基础的，因此，证据理论的推理过程是首先求出结论的概率分配函数，然后再求出结论的信任函数和似然函数，从而得出结论的信任度[7-9]。

可信度方法是基于概率论一种不确定性推理方法。在某一专业领域中很难用较精确的数据模型来进行描述，并且应用先验概率及条件概率有时也比较困难，所以用可信度来表示知识及证据的不确定性则是一种相对较好的方法[10]。

在基于可信度不确定推理模型中，知识是以产生式规则的形式来表示的，引入可信度后，其一般的表示形式为：IfEthenH(CF(H,E))，式中，E是知识的前提条件或称为证据，它既可以是一个简单条件，也可以是用and及or把多个简单条件连接起来所构成的复合条件；H是结论，它可以是一个单一的结论，也可以是多个结论；CF(H,E)是该条知识的可信度，称为可信度因子或规则强度。

除了知识的不确定性外，在不确定性推理中证据的不确定性表示也非常重要，按照证据的个数不同其获取方法分为单个证据的不确定性获取方法和组合证据的不确定性获取方法。

1)单个证据的不确定性获取方法 在不确定性推理中，如果支持结论的证据只有一条，则其可信度值一般可由用户直接给出。

2)组合证据的不确定性获取方法 如果支持结论的证据有多个，则按照证据间的关系来进行求取。

①合取关系E=E1∧E2∧E3∧…∧En，即取其中可信度最小的证据。

②析取关系E=E1∨E2∨E3∨…∨En，即取其中可信度最大的证据。

不确定性的推理计算是从不确定性的初始证据出发，通过运用相关的不确定知识来推导出结论的可信度值。如果支持结论的知识只有一条，且证据E的可信度CF(E)和规则强度已知，则结论H的可信度计算公式：

CF(H)=CF(H,E)×max{0,CF(E)}

(1)

如果支持结论的知识有多条时，由于多条知识的综合可通过两两的合成来实现，所以先考虑2条知识的情况，则这时结论H的可信度的公式如下：

(2)

CF1(H)=CF(H,E1)×max{0,CF(E1)}CF2(H)=CF(H,E2)×max{0,CF(E2)}

(3)

2 带有比较因子的加权可信度推理方法

2.1CWR推理模型

在基于可信度的推理方法中，人们总是主观的认为已经存在或发生的事实证据对结论的支持程序都是相同的。其实不然。如：If流量波动增大 and 管线泄漏检测装置发生报警then发生管道泄漏事故。在这一条规则中，管线泄漏检测装置发生报警这一条证据对结论的支持程序远远大于前一证据，所以当这一证据出现时，流量波动是否增大已经不重要了，可以直接判断管道泄漏事故已经发生。

针对这一种情况，笔者在可信度推理模型的基础上，对支持结论的证据引入加权因子，构造加权可信度推理模型(CWR)，通过加权因子来说明证据对结论的支持程度，从而提高推理精度。

CWR推理模型表述如下：

Ife1(w1)∧e2(w2)∧…∧en(wn) thenH(CF(H,e),λ)

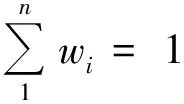
应该根据证据对结论的支持程度给出权值。证据相对独立且对结论支持较大时，证据所具有的权值较高。相反，证据对结论的支持度越小，权值也就越低。

在常规的产生式规则中，只有发生的事实证据与规则前件中已有证据完全符合时，才能推导出结论，而应用上述模型可以有效的解决证据不完整时的推理问题。当根据已知的事实证据可信度计算出来的组合证据可信度大于阈值时，就可以激活该规则，并推导出结论。

然而，当证据过多时，仍然采用上述推理模型，计算组合证据的可信度就会浪费大量的时间，虽然推理精度可以保证，但推理速度就会大大降低。如在油田生产中，事故发生时所表征出来的事故现象有些时候是多种多样的，所以在规则库中支持结论的证据会很多。针对这一问题的产生，笔者在加权可信度推理方法基础上引入比较因子，形成带有比较因子的加权可信度推理模型(CCWR)。

2.2CCWR推理模型

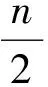
CCWR推理模型如下：

Ife1(w1)∧e2(w2)∧…∧en(wn) thenH(CF(H,e),λ,μ)

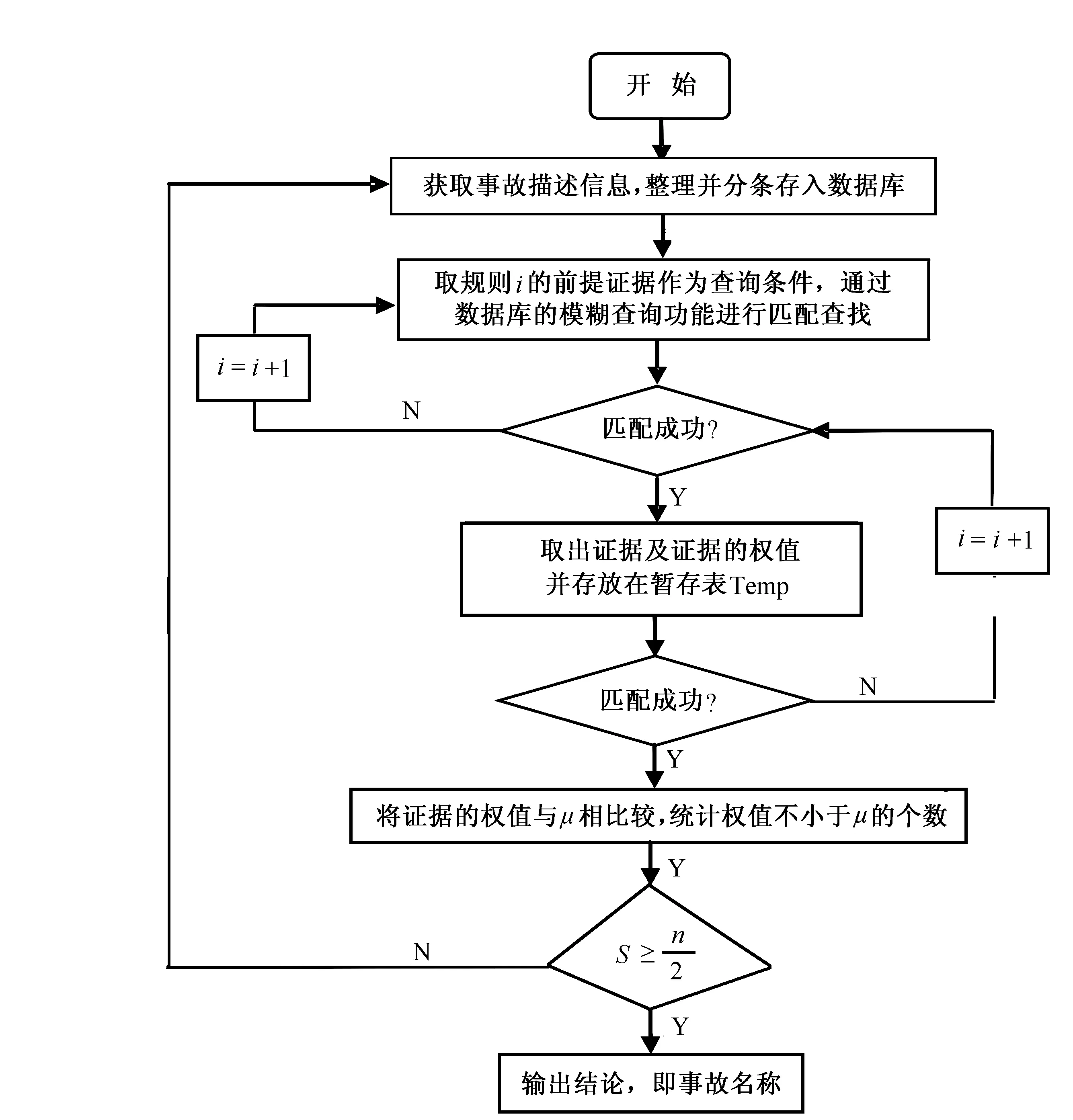
图1 CCWR不确定推理流程图

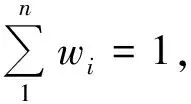
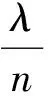
CCWR推理流程如图1所示。

3 实例分析

在油田生产应急指挥规则库中有这样一条加权规则：If 电源全停 (0.25) and 照明全停 (0.25) and 仪表指示失效 (0.15) and继电自动保护装置动作停止 (0.25) and 开关信息全无 (0.1) then 发生变电所失电事故(0.99，0.8，0.16)。

若现在根据现场人员汇报上来的事故描述在综合数据库中只有如下证据：电源全停CF(e1)=1，照明全停CF(e2)=1，仪表指示失效CF(e3)=0.9，继自装置动作停止CF(e4)=1。

3.1推理方法1：采用CWR模型

组合证据的可信度：

已知λ=0.8，由CF(E)>λ可知该规则已经被激活，CF(H,E)=0.99。

结论可信度：

CF(H)=CF(H,E)×max{0,CF(E)}=0.99×0.885=0.87615由此可以判断“发生变电所全所失电事故”的可能性为87.615%，可认为已发生事故。

3.2推理方法2：采用CCWR模型

由带有比较因子的加权可信度推理模型可知μ=0.16；将证据的权值与比较因子进行比较：

w1>μw2>μw3>μw4>μ

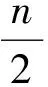
通过2种方法的比较，明显可以看出带比较因子的加权可信度推理更方便快捷有效。

4 结 语

在比较几种常用的不确定性推理方法的基础上，提出了带比较因子的加权不确定性推理模型(CCWR)，并给出了这种模型的推理方法。实例分析表明应用CCWR推理方法可以在维持原有精度的前提下有效地提高推理速度。

[1]高鹰，谢胜利.免疫粒子群优化算法[J].计算机工程与应用，2004,40(6)：4-6.

[2]刘洁.基于不确定信息处理的机器人地图创建[D].吉林：东北电力大学，2006.

[3]利珊.不确定性中的随机性和模糊性[J].金华职业技术学院学报，2010,10(3)：46-48

[4]于少伟.基于云理论的新的不确定性推理模型研究[J].山东大学学报(理学版)，2009，44(3)：84-87.

[5]孟福真.不确定性矿配问题的优化方法研究[D].长沙：中南大学，2009.

[6]杜江，任滢.故障智能诊断专家系统模型研究[J].光电技术应用，2009,24(4):73-79.

[7]胡睿.钻井工程事故诊断专家系统研究[J].中国石油大学胜利学院学报，2010,24(3):14-18.

[8]李德毅，杜鷁.不确定性人工智能[M].北京：国防工业出版社，2005.

[9]卢丹丹.基于人工智能的大学英语辅导教学专家系统[D].北京：北京化工大学，2009.

[10]陈颖，徐晓晖，李志全.基于免疫克隆原理的改进粒子群优化算法的研究[J].系统仿真学报，2008，20(6)：1471-1474.

10.3969/j.issn.1673-1409(N).2012.08.043

TP202.4

A

1673-1409(2012)08-N131-03

2012-05-20

黑龙江省教育厅科学技术研究项目(12511014)。

康朝海(1976-)，男，1998年大学毕业，硕士，讲师，现主要从事复杂系统的优化控制及故障诊断的方面的教学与研究工作。

张东旭(1984-)，男，2007年大学毕业，硕士，工程师，现主要从事智能控制及地理信息系统的应用方面的研究工作;E-mail:25327109@qq.com。

[编辑] 洪云飞