自行加榴炮药温精确测量研究

陆 欣，周彦煌，余永刚，陈劲操

(南京理工大学 能源与动力工程学院, 江苏 南京 210094)

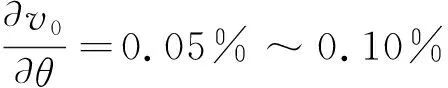
1 影响药温测量精度的因素分析

自行加榴炮的装药，其外形近似圆柱体，外部为药筒或包装筒，内部有钝感衬里、点传火组件及其它装药辅助元件，药粒散装或分成药包放于药筒内。在野战条件下，装药通常都处于热的非平衡状态，装药温度场为非稳态温度场，装药温度随环境温度的波动不断变化。可见，装药温度场与发射装药的组成结构、几何特性和物理特性有关，还与所处环境及初始条件有关。自行加榴炮计算射击诸元时所需的药温是指发射药的实时平均温度，即装药温度场的质量加权平均值。因此，用测量药筒表面或内部某一点的温度作为药温是无法满足精度要求的。根据以上分析，可以看出影响药温测量精度的因素主要包括：

1)装药温度场的质量加权平均值。由于装药温度场是非稳态的，平均药温随时间不断变化，为弹道解算提供的药温必须是装药温度场的实时平均值，这是保证药温测量精度的关键因素。

2)装药结构的几何特性和物理特性。装药的几何特性应考虑形状、尺寸和装药组成元件放置的部位；物理特性则包括火药品号、药量及装药元件的热物理特性，从而充分体现出药温与装药型号的相关性。

3)装药环境温度的非均匀性。野战条件下，装药环境温度不但随时间变化，而且在空间上也不可能完全一致，即使是车体内的药仓环境也是如此。因此，装药环境温度的非均匀性也是影响药温测量精度的一个重要因素。

4)装药初始温度。从传热理论可以知道，装药温度场不仅受环境条件影响，而且与初始条件也密切相关。装药初始温度设置的不准确将会导致在随后的一段时间内解算的药温出现较大偏差。因此，药温的精确测量也要保证装药初温的准确性。

2 装药的非稳态热传导模型及数值分析

发射装药可以看成是由多层壁面组成的多孔介质圆柱体，外壳为药筒，向内依次是钝感衬里和药包与筒壁之间的空气夹层, 主体是药粒堆积而成的多孔介质，中心为传火管。此发射装药的传热过程可用二维轴对称圆柱体的非稳态导热模型描述，微分方程为:

(1)

式中：θ为温度；ρ、c和λ分别为物质的密度、比热容和导热系数。

为了求解上述偏微分方程，还应给出初始条件和边界条件。取装药进入车体药仓时刻的温度作为初始药温，初始条件可以表示为:

θ(x,r,t)|t=0=θ(x,r,0)=θ0

(2)

考虑装药与外界环境的换热过程为自然对流，则边界条件为:

(3)

式中：n表示装药表面的外法线方向;α为表面换热系数;θw为药筒表面温度;θf为外界环境温度。

通过上述方程求得装药温度场中任意一点的温度θ(x,r,t)，则装药温度场的质量加权平均值可用如下表达式计算:

(4)

为了计算上述二维轴对称非稳态导热方程所描述的装药温度场分布，需要采用有限差分数值方法对偏微分方程进行离散化处理。本文采用控制容积法[3]，在时间间隔[t，t+Δt]内对装药中任一点积分，有:

(5)

假定非稳态项中温度随时间和空间都是阶梯形变化, 扩散项中则随空间分段线性变化, 随时间阶梯形变化, 并采用隐式格式, 则式(5)的积分结果如下:

(6)

对于Δx=Δr的均匀网格，式(6)可以写为:

(7)

装药平均温度的计算公式为:

(8)

式中：M、N分别表示径向和轴向的网格节点数。

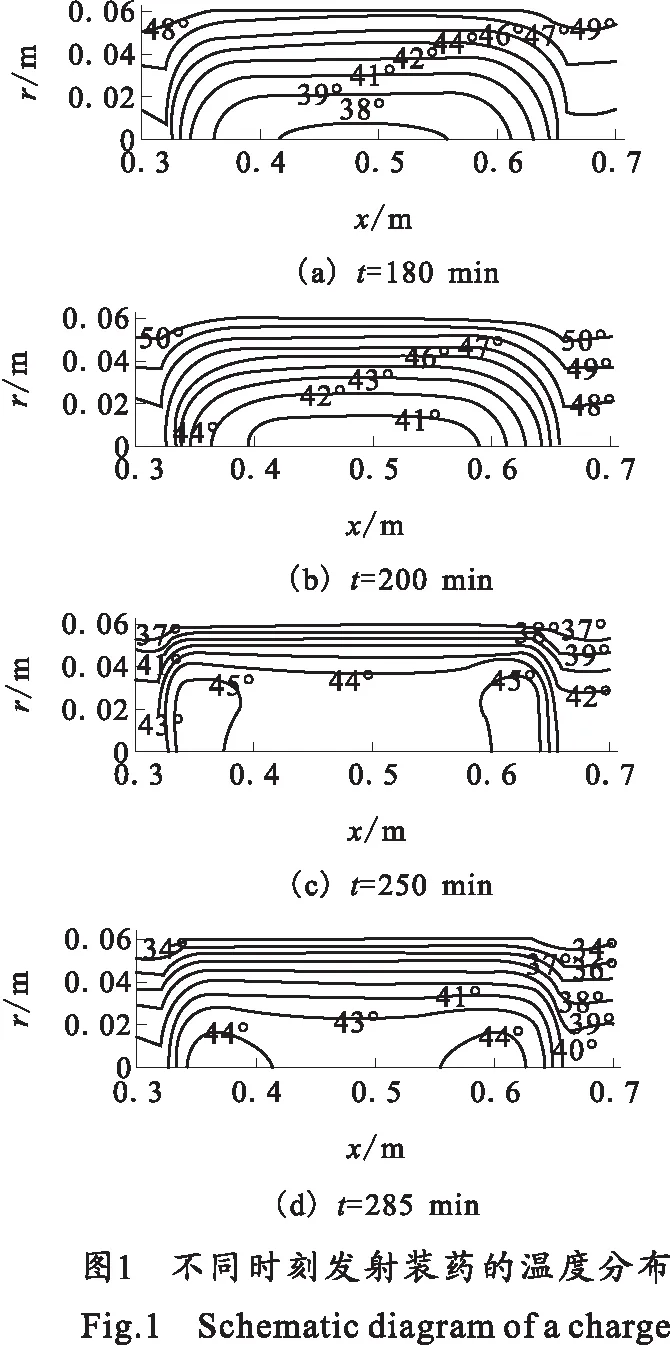
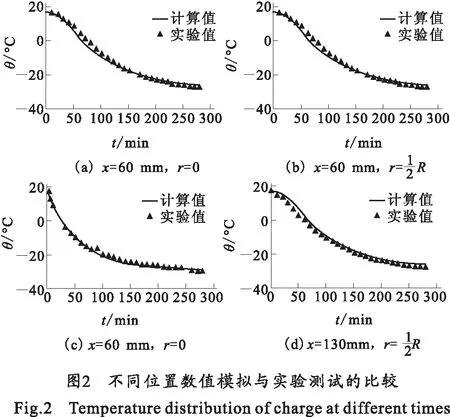
利用上述离散后得到的差分格式组成的代数方程组对装药温度场进行了数值模拟。图1给出了不同时刻实际装药区域的温度分布。图2是不同位置数值计算结果与实验测试结果的对比，实验是在实际装药内沿轴向和径向布置测试点，在这些测试点放置热电偶测量相应位置的发射药温度随时间的变化规律。从图中可以看出计算结果与实验结果吻合很好，说明所建的物理模型、采用的计算方法和调试的热物理参量是正确的，为研发非接触式全自动药温在线测量装置奠定了基础。

3 非接触式全自动药温在线测量装置的研发

在研究了发射药传热特性和建立了描述药温变化规律的非稳态热传导模型的基础上，本文为155 mm自行加榴炮开发了一种非接触式全自动药温在线测量装置，可对车内不同型号装药实现装药温度场和实时平均温度的精确测量。该测量装置的组成及工作原理如图3所示。

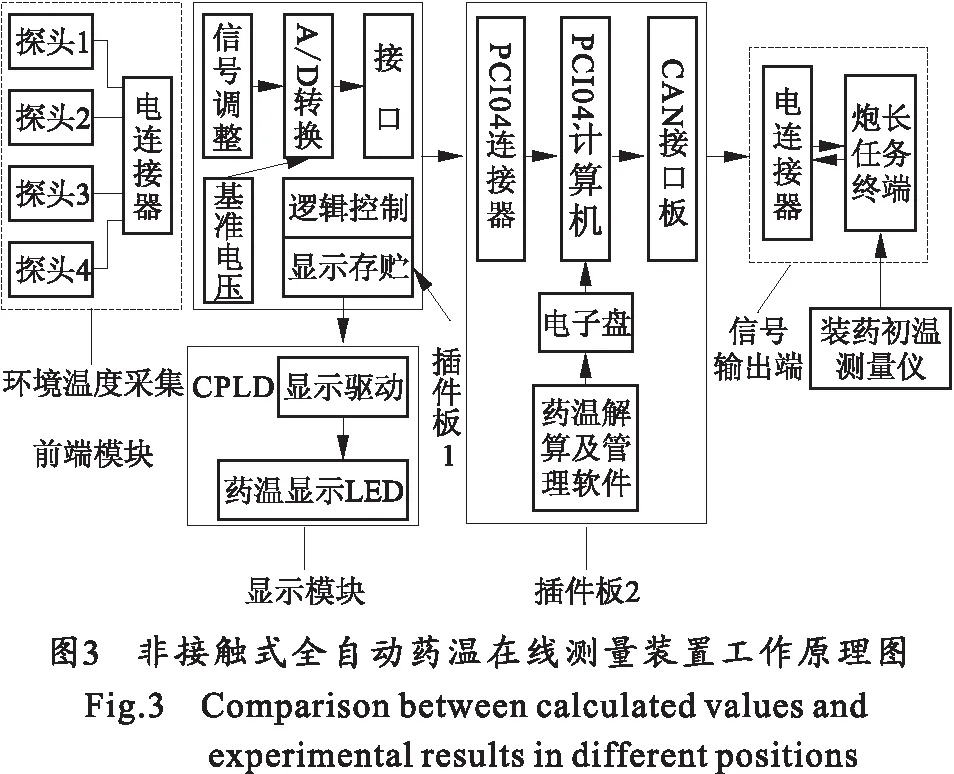
由图3可见，装置测量获得的温度信息通过CAN总线接口与炮长任务终端实现信息自动传输，时刻供弹道解算和诸元修正使用。本装置主要有主机和环境温度传感器电缆组成(见图4)，主机包括PC104计算机、CAN总线接口板、专用温度解算软件、电源模块和显示模块等。PC104计算机是装置的核心硬件，负责系统的运行、管理及与上位机炮长任务终端的通信。专用温度解算软件建立在装药非稳态热传导方程基础上，利用对抛物型偏微分方程离散化并运用有限差分方法得到的计算模型实现温度场的数值求解，再经过质量加权后得到药温的实时平均值。环境温度传感器则用来采集药仓内的空气温度，为专用温度解算软件提供计算装药温度场的边界条件。

图4是本非接触式全自动药温在线测量装置的实物照片。测量装置上电后，首先进行自检，之后自动进入工作状态，通过环境温度传感器采集药仓内的环境气温，确定出求解描述装药温度场的非稳态热传导方程所需的边界条件，初始药温则由炮长任务终端确定并通过CAN总线通信传输获得，专用温度解算软件得到初始条件和边界条件后就可以不断给出装药的温度分布和药温的实时平均值。环境温度传感器每隔3s采集一次药仓内的环境气温并提供给专用温度解算软件，因此得到的药温反应出了装药温度随环境温度的变化过程。检验和精度考核结果表明，本测量装置精度高、响应快、通信传输正确无误，能够用于自行加榴炮武器系统为弹道解算提供实时药温。

4 结 论

本文在分析发射药传热特性的基础上，建立了描述药温变化规律的非稳态热传导模型，数值模拟结果表明所建的物理模型、采用的计算方法和调试的热物理参量是正确的，可以反应装药温度随环境温度的实时变化过程。研制的非接触式全自动药温在线测量装置精度高、响应快，并能通过装置上的通讯接口将测量结果实时传输给火控系统的炮长任务终端，满足了自行加榴炮武器系统对数字化和信息化的要求。

[1] 周彦煌, 余永刚, 陈劲操. 现代箭炮装药实时温度精确测量的研究[J]. 弹道学报, 2001, 13(1): 56-61.

ZHOU Yan-huang, YU Yong-gang, CHEN Jin-cao. Significance and necessity of real-time precision measure of charge temperature for modern artillery and rocket[J]. Journal of Ballistics, 2001, 13(1): 56-61. (in Chinese)

[2] 郭锡福. 远程火炮武器系统射击精度分析[M]. 北京: 国防工业出版社, 2004.

GUO Xi-fu. Firing accuracy analysis for long range gun weapon systems[M]. Beijing: National Defense Industry Press, 2004. (in Chinese)

[3] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001.

TAO Wen-quan. Numerical heat transfer[M]. Xi’an: Xi’an Jiaotong University Press, 2001. (in Chinese)