基于模糊Petri网的某型舰炮系统故障诊断

张凌海, 王学军,王 青

(1.海军工程大学 兵器工程系, 湖北 武汉 430033；2.青岛4308机械厂，山东 青岛 266000)

某型舰炮结构复杂，自动化程度高，系统内外关联紧密和在实际使用过程中经常会出现各种故障。为防止贻误战机，保障其持续作战能力，系统故障诊断和排除就显得尤为重要。

Petri网最早是由德国Petri博士于1962提出的一种可以用于离散时间系统建模和分析的有效工具[1]，之后，Zisman M D将Petri网用于产生式规则系统[2]， Looney C G将知识表示的概念引入模糊Petri网[3]，Chen S M等在此基础上提出了基于Petri网可达图的模糊推理算法[4]，高梅梅等给出了此推理算法的形式化数学算法[5]，近几年该算法在故障诊断方面有了广泛的应用。

本文首先介绍了某型舰炮的故障类型及故障的规则表示，然后引入模糊网及其推理算法，结合舰炮故障实例建立模糊Petri网模型并进行推理计算，取得了较好效果。

1 某型舰炮故障的类型及表示

1.1 某型舰炮故障状态的类型

当舰炮处于不允许启动的非正常状态或处于会导致设备损坏状态时，系统的电器联锁控制、计算机控制系统和武器逻辑控制系统会根据设备状态和炮弹位置所反馈的信号进行判断，对舰炮实施紧急制动，使舰炮处于“故障”状态。因此，舰炮在工作过程中，由于机械、电气或液压部分失效或操作失误等均可能导致舰炮处于“故障”状态。根据故障出现的部位可以将“故障”分为以下7种状态：补供弹系统故障、随动系统故障、发射系统故障、液压系统故障、供电系统故障、补供弹系统报警和瞄准随动系统报警。

1.2 故障的规则表示

故障现象与故障原因之间的关系不但具有模糊性还具有传播性，一个或多个故障的产生会导致出现另一个或多个故障，在这里故障之间的模糊关系以及传递关系可以用模糊产生式规则来描述。假设R为一模糊产生式规则集，R={R1，R2，…，Rn}，其中Ri为R中的第i条规则，则Ri可用下式描述[6]：

Ri=IFdjTHENdk(CCF=μi)

其中，dj、dk表示系统状态特征的命题，在这里就是两种故障状态，CCF是这条规则的置信度，其值为μi，取值大小在0到1之间。这条规则可以理解为由故障dj导致故障dk产生的可信程度为μi。

上述规则为单输入单输出的模糊规则，是最简单的模糊规则。对于多输入多输出的模糊规则，可将其分解为多输入单输出的模糊规则，按照其多输入的类型可以将基本的故障产生式规则分为以下两种：

“与”规则 故障d1，d2，…，dn同时出现可能导致故障d的出现，即：

Ri=IF(d1andd2and …anddn)THENd(CCF=μi)

“或”规则 故障d1，d2，…，dn中的一种或几种出现可能故障d的出现，即：

Ri=IF(d1ord2or …ordn) THENd(CCF=μ1，μ2，…，μn)

其中μ1，μ2，…，μn与d1，d2，…，dn是一一对应的。

其Petri网表示形式如图1所示，可以看到“或”规则中包含了多个变迁。通常情况下舰炮武器系统的故障产生式规则多为“或”规则。

2 模糊Petri网

2.1 模糊Petri网的定义

模糊Petri网是在基本Petri网基础上拓展而来的，其库所、变迁以及流关系与普通Petri网都相同，只是所代表的意义不同。其框架代表基于产生式规则的知识结构，库所代表命题，库所上表示的托肯值代表命题为真的置信度，规则的推理过程用网中带置信度的变迁表示，命题之间的因果关系用库所和变迁之间的有向弧表示。在模糊Petri网中有以下几点不同于传统Petri网：

1)库所中的托肯值代表命题的真实度，因此，其大小位于0到1之间。

2)规则的触发意味着命题为真的繁衍，触发以后命题的输入库所的真值不变。

3)不存在普通Petri网中并发冲突的问题。

模糊Petri网(FPN)有很多不同的形式，本文采用基本模糊Petri网，它可以定义为一个6元组。

∑FPN=(P,T,I,O,f,θ)

其中：

P={P1,P2,…,Pn}表示命题的有穷集合；

T=(t1,t2,…,tn)表示变迁的有穷集合，即规则的点火触发；

I[O]：T→P∞表示输入(输出)函数，反映了变迁到输入(输出)命题的位置；

f：T→[0,1]是一个映射，反映变迁的可信度；

θ：P→[0,1] 是一个映射，反映命题的可信度。

2.2 模糊Petri网的推理算法

用数学形式将模糊Petri网中的信息表达出来。Δ为输入函数矩阵I(P→T)，Δ={δij}，δij为逻辑量，δij∈{0,1},当Pi是Ti的输入时，δij=1，否则δij=0(i=1，2，…，m，j=1，2，…，n)；Γ为输出函数O(T→P)的矩阵，Γ={γij}，γij为逻辑量，γij∈{0,1}，当Pi是Ti的输出时，γij=1，否则，γij=0(i=1，2，…，m，j=1，2，…，n)；U为变迁的置信度矩阵，U=diag(μ1，μ2，…，μn)，μi为变迁ti的置信度。

本文的推理算法为MYCIN的置信度方法，“与”规则的输入采用各输入的最小值，“或”规则的输入采用各输入的最大值。为方便进行计算，引入几个极大代数算子：

⊕:a⊕b=c,a,b,c为n维向量，则ci=max{ai,bi}；

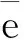
为方便表示，这里设几个中间变量[5]：

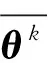
其中，k表示推理步数；θk为m维向量，表示在第k步中每个命题为真的置信度；neg(θk)表示在第k步中每个命题为假的置信度；νk为n维向量，表示变迁tj的前提为假的可信度(j=1，2，…，n)；ρk表示变迁tj的前提为真的可信度(j=1，2，…，n)，这个表达式的意思就是当一个变迁有多个输入命题(即为“与”规则)时，取置信度最小的输入命题作为变迁的输入命题。

根据模糊Petri网的特点，命题P的下一步的状态θk+1应为：

θk+1=θk⊕[(Γ·U)]⊗ρk

其中[(Γ·U)]⊗ρk表示同一个输出命题取其输入变迁的最大值，并令其输入命题托肯值置零，再与θk取⊕运算是为是使变迁触发以后输入命题置信度不变。

由此，可得推理算法：

步骤1.令k=0；

步骤2.根据式(1)求k+1；

步骤3.若θk+1≠θk，令k=k+1，重复步骤2；若θk+1=θk，推理结束。

3 基于模糊Petri网的舰炮故障诊断

以某型舰炮弹药盘点异常故障为例，其故障类型及传播方式主要有以下几个：

1)如果炮弹序列不连续P1或有弹传感器故障P2或电气插件故障P3，则可能出现炮弹数错P7，其置信度分别为0.93，0.98，0.90。

2)如果有弹传感器故障P2或电气插件故障P3或软件错误P4或机械凸轮与杠杆连接异常P5则可能出现计算机显示异常P8，其置信度分别为0.98，0.90， 0.96，0.92。

3)如果机械凸轮与杠杆连接异常P5或凸轮箱故障P6，则可能出现机械故障P9，其置信度分别为0.92，0.94。

4)如果炮弹数错P7或计算机显示异常P8或机械故障P9，则可能出现弹药盘点异常，其置信度分别为0.93，0.95，0.90。

用模糊产生式规则表示为：

IFP1orP2orP3THENP7(CCF=0.93，0.98，0.90)；

IFP2orP3orP4orP5THENP8(CCF=0.98，0.90，0.96，0.92)；

IFP5orP6THENP8(CCF=0.92，0.94)；

IFP7orP8orP9THENP10(CCF=0.93，0.95，0.90)；

根据以上规则建立的模糊Petri网模型如图2所示。

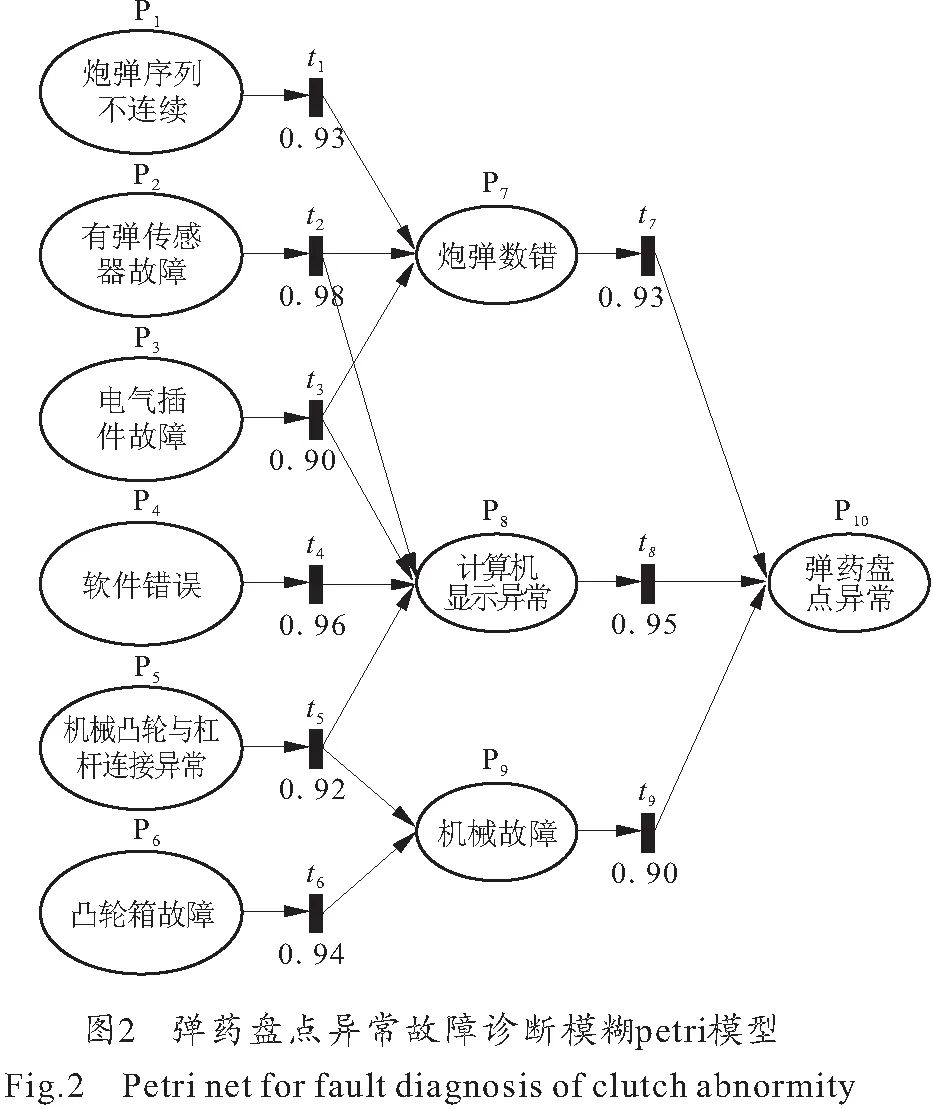
此时，输入输出矩阵分别为：

U=diag(0.93，0.98，0.90，0.96，0.92，0.94，0.93，0.95，0.90)；

设初始状态为：

θ0=(0.38，0.45，0.56，0.20，0.67，0.80，0，0，0，0)T。

由推理算法得：

θ1=(0.38，0.45，0.56，0.20，0.67，0.80，0.50，0.62，0.75，0)T。

θ2=(0.38，0.45，0.56，0.20，0.67，0.80，0.50，0.62，0.75，0.68)T。

θ3=(0.38，0.45，0.56，0.20，0.67，0.80，0.50，0.62，0.75，0.68)T。

由于θ2=θ3，故推理结束。弹药盘点异常的概率为0.68。从推理的过程可以看出，模糊Petri网的推理过程很好地体现了故障的传播过程，且具有并行性和模糊性，推理的步数与故障的传播深度直接相关，规则的多少并不直接影响推理的过程。

4 结 论

在对某型舰炮进行故障诊断时，利用模糊Petri网能有效地描述故障之间的传播关系，建立的图形化模型具有直观性，清晰易懂，充分体现了模糊Petri网描述系统动态性、并行性的能力，推理的过程也很好地反映了故障传播的模糊性。通过本文可以看出，在某型舰炮故障诊断系统中使用模糊Petri网进行推理诊断是行之有效的。

[1] 袁崇义．Petri网原理与应用[M]．北京：电子工业出版社，2005：2-6．

YUAN Chong-yi．Principles and applications of petri-net[M].Beijing：Publishing House of Electronics Industry，2005：2-6．(in Chinese)

[2] ZISMAN M D，Use of productiong system for modelling asynchronous concurrent processes[J]．Pattern Directed Inference Systems，London：Academic Press，1978:53-68．

[3] LOONEY C G．Fuzzy petri-nets for rule based decision-making[J]． IEEE Translations on Systems，Man And Cybernetics，1988，18(1)：178-183．

[4] CHEN S M．Knowledge representation using fuzzy petri-nets[J]．IEEE Translations on Knowledge and Data Engineering，1990，2(3)：311-319．

[5] 高梅梅，吴智铭．模糊推理Petri网及其在故障诊断中的应用[J]．自动化学报，2000，9(26)：677-680．

GAO Mei-mei，WU Zhi-ming．Fuzzy reasoning petri net and its application fault diagnosis[J]．Acta Automatic Sinica，2000，9(26)：677-680． (in Chinese)

[6] 张博，窦丽华，陈杰，等．一种基于模糊Petri网的操瞄系统故障诊断方法[J]．北京理工大学学报，2008，9(28)：790-793．

ZHANG Bo，DOU Li-hua，CHEN Jie，et al．A method for diagnosis in aiming systems based on fuzzy petri net[J]．Transactiongs of Beijing Institute of Technology，2008，9(28)：790-793．(in Chinese)