臂式输弹机的结构设计和仿真分析

曲振森, 薄玉成, 王惠源,曲 普

(中北大学 机电工程学院，山西 太原 030051)

国内外先进的自行火炮都广泛采用了自动或半自动的输弹机构，与人工装填相比，用输弹机构装填弹药，首先可以减轻炮手的劳动强度，其次可以解决高角射击时人工装填困难的问题，再次还可以保证较好的装填一致性，有利于提高火炮的射击精度。鉴于输弹机构装填弹药对火炮射速和射击精度的提高，对输弹机构的研究一直都具有重要的意义[1]。

1 臂式输弹机的结构及工作原理

如图1所示，输弹机构的主体结构采用的是齿轮结构，图中圆代表齿轮[2]。太阳轮1固定在托弹架8的侧板上不转动；摆臂a端与太阳轮中心连接，可绕太阳轮中心(a端)自由转动；惰轮2连接在摆臂上与太阳轮啮合，且能够自由转动；行星轮3连接在摆臂的b端并与惰轮啮合，也可以自由转动；输弹臂5的一端与行星轮固连，随行星轮转动；为了减小工作时输弹臂c端与弹底的摩擦力可在c端加上输弹轮6。

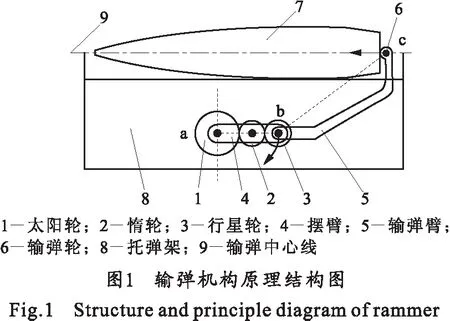
如图1的方向箭头所示，输弹机构工作时，电机驱动主动元件，由于各构件之间的相互约束，摆臂的b端就沿箭头方向转动，输弹臂在随摆臂转动的同时，其c端始终保持在输弹中心线上并按图中箭头方向运动。

当摆臂5转过90°，也就是直线ab处于竖直位置时，输弹臂也运动到位，此时输弹臂端点连线bc与摆臂中心线ab重合，推弹动作完成，弹丸进入惯性输弹行程，输弹机构运动构件复位。由于输弹机构完成一次输弹的动作(初位置→推弹→复位)的过程，与人手臂的蜷缩和伸展动作相似，故为该机构取名为臂式输弹机构。

该机构功能的实现，最关键的部分在于太阳轮和行星轮之间的传动比，传动比的确定要保证当摆臂4的端点连线ab转动至竖直位置时，输弹臂5的端点连线bc与之重合。只有确定了恰当的传动比，才能通过齿轮间的约束关系，使输弹轮的中心始终在输弹中心线上，从而保证弹丸的受力点和运动过程中受到的推力方向不变。

2 输弹机构的仿真及结果分析

2.1 输弹过程分析

输弹的整个过程分为强制输弹行程和惯性输弹行程，强制输弹行程是输弹机构对弹丸作用的过程，惯性行程是强制输弹结束后弹丸靠惯性继续运动直至定位的过程。要保证较好的装填一致性，避免“恒力”输弹对火炮射击精度的产生的不利影响，在不同射角时需要的强制输弹力是不同的[3]。

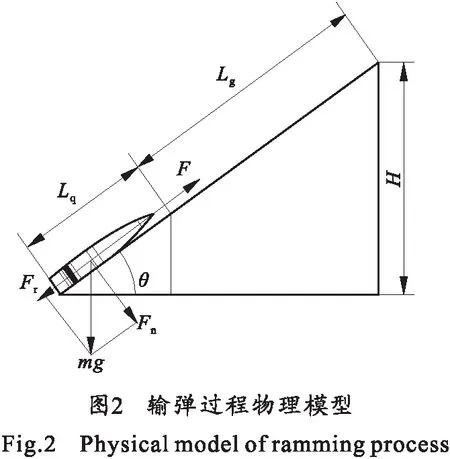
如图2所示，建立输弹过程的物理模型，其中:F为弹丸受到的强制输弹力;Lq为强制输弹行程;Lg为惯性输弹行程;H为弹丸上升的高度;Fn为弹丸重力垂直输弹中心线分力;Fr为弹丸重力在输弹中心线上的分力;Fr对弹丸进行受力分析，于是有：

Fn=mgcosθ

(1)

Fr=mgsinθ

(2)

由机械能守恒定理得出：

FLq-mgsinθ(Lq+Lg)-μmgcosθ(Lq+Lg)=

(3)

(4)

式中:θ为火炮射角;m为弹丸质量;μ为摩擦系数;vq为强制输弹结束时弹丸的速度;vk为弹丸定位所需的卡膛速度。

由公式(3)、(4)得：

(5)

(6)

输弹过程中强制输弹时间为T1，惯性输弹时间为T2：

(7)

(8)

由以上分析，在给定θ的值时，用公式(5)计算得到的F值是一个固定值，当结合到臂式输弹机构本身时，在强制输弹阶段又有自己的特点。

如在第1部分中说明的一样，要实现机构的功能，在图3中必须满足两个基本条件：

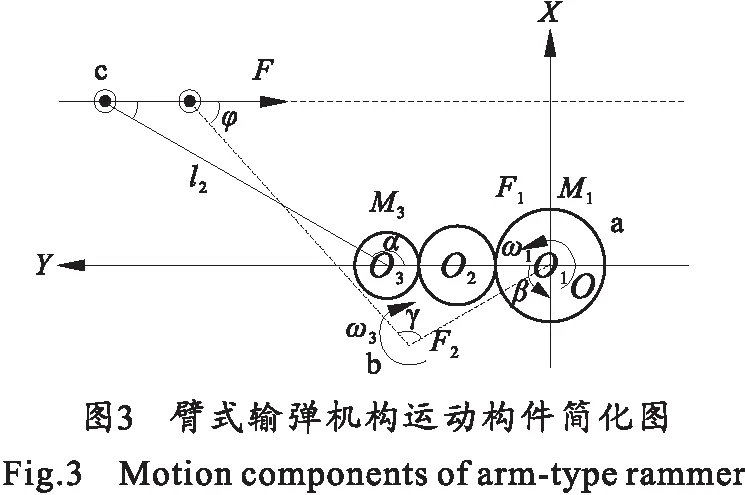
1)太阳轮O1与行星轮O3的传动比应满足：

i13=ω1/ω3=β/α

(9)

式中:ω1为摆臂转动的角速度;ω3为输弹臂绕圆心O3转动的角速度;α为初始位置摆臂与输弹臂的夹角;β为推弹动作结束时摆臂转过的角度。

2)输弹臂l2与摆臂l1的长度应满足：

l2-l1=e

(10)

式中：e为O1到输弹中心线的垂直距离。

当在摆臂a端施加图中所示的转矩M1时，由力平衡的知识可得：

(11)

由图3可以求得：

φ=π-[α-ω1t(i31-1)]

(12)

则式⑼可转化为：

(13)

式中:λ=l1/l2;ω1为摆臂绕O1转动的角速度。

则强制输弹行程中，弹丸在输弹中心线上的运动微分方程为：

(14)

式中:Lg(t)为弹丸强制输弹行程中的位移函数;F(t)为推弹力函数。

由式(13)可知，臂式输弹机构在主动构件转速一定时，提供给弹丸的推力F不是一个定值，而是随时间变化的，在不考虑能量损失的前提下，力F做的功等于力矩M1做的功：

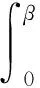
(15)

则消耗的功率为：

(16)

式中：T1=β/ω；β(t)为摆臂转动的角度函数。

2.2 输弹机构仿真

以122 mm口径的弹丸的输送为例，当给定l1=150 mm、λ=0.5，则l2=300 mm、α=5π/6，i13=3∶5，在μ=0.2，m=22，vk=2.5 m/s时,由公式(6)可得不同射角下vq的值(见表1)。

表1 不同射角下vq的数值

根据结构原理计算出其他零件尺寸，建立臂式输弹机构的虚拟样机[4]。为了保证摆臂和输弹臂等零部件在工作状态下受力均衡和输弹机构动作稳定，建立模型时选择使用了对称结构。

通过接口模块将输弹机构的虚拟样机和弹丸导入仿真软件，赋予弹丸和输弹机构各部件材料属性，仿真软件会自动计算出它们的质量、惯性矩和质心等物理信息。利用布尔运算，把没有相对运动的构件简化为一个刚体，为各个构件之间添加必要的运动副和接触，并在主动件上添加驱动，进行动力学仿真[5-6]。仿真是在摩擦系数、刚度系数等一系列参数不变的条件下，从两个方面进行：

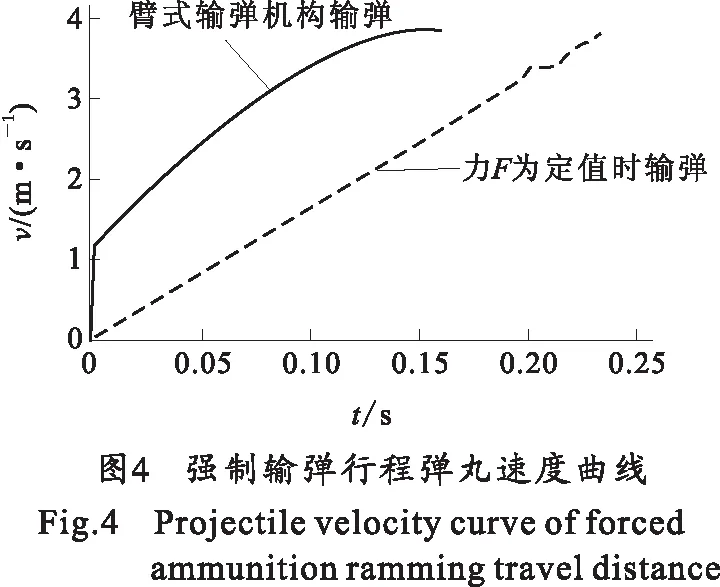
1)在0射角时，强制输弹行程相同与强制输弹行程结束时弹丸获得速度相同的情况下，分别对用恒力F推弹和用臂式输弹机构输弹进行仿真，仿真结果如图4、图5所示。

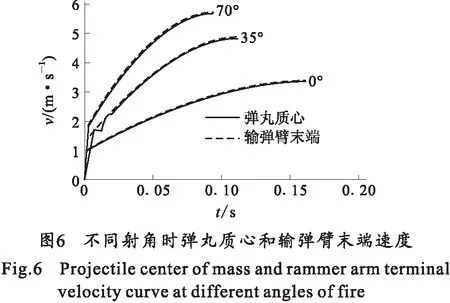
2) 在强制输弹行程相同的情况下，分别在射角为0°、35°和70°时，对输弹机构输弹进行仿真，仿真结果如图6所示。

2.3 仿真结果分析

1) 由图4可知，在推弹位移一定和推弹完成时弹丸获得速度相同的情况下，臂式输弹机构输弹完成输弹动作所需的时间要比力F为定值时沿输弹中心线推弹所需的时间短，这对缩短整个输弹时间乃至提高射速是有积极意义的。

2)从图5中可以看到，在整个强制输弹行程中除了起始阶段，弹丸质心的速度曲线和输弹臂末端的速度曲线基本上重合。从图6中也不难发现，在不同射角时，当弹丸的速度开始稳定增加后，输弹臂末端与弹丸的速度曲线也是基本重合的。这就说明在不同射角下输弹轮都能与弹丸接触良好，不会发生明显脱离，这将有利于弹丸的稳定加速。

3)需要说明的是，就图6来看，在不同射角下，弹丸速度曲线在起始阶段都会出现跳跃的现象，之所以会出现这种现象，主要原因是主动构件的转速不是从0开始逐渐增加到某一稳定值，而是从零时刻到仿真结束始终保持某一定值，而弹丸的速度则需要从0开始增加，弹丸在瞬时获得很大加速度，速度急剧增加。

4)关键的一点，从图5中可以看出，弹丸质心的加速度曲线在弹丸速度稳定增加后没有较大的波动，结合图6中输弹臂末端的速度曲线也可以得出，在主动件转速恒定的状态下，输弹臂末端的速度是在逐渐增加且没有较明显的波动，这就证明了该臂式输弹机构对弹丸的加速和运动稳定更加有利。

3 结 论

输弹机构是火炮输弹系统的重要组成部分，输弹机构的工作状态将直接影响到整个输弹系统的输弹效果，本文通过对臂式输弹机构的建模和仿真分析，阐明了该机构的显著特性，说明了该输弹机构对大中口径火炮的半自动输弹机构的设计及优化有着积极的意义。

[1] 梁辉，马春茂，潘江峰，等.大口径火炮弹药自动装填系统研发现状和趋势[J].火炮发射与控制学报，2010(9)：103-107.

LING Hui, MA Chun-mao, PAN Jiang-feng,et al.Current situation and development trend of autoloaderin large caliber howitzer[J].Journal of Gun Launch & Control, 2010(9):103-107.(in Chinese)

[2] ADOLF NORDMANN, HOCHDAL, GERMANY. Rammer for projectiles: U.S,3938421[P].Foreign Application Priority Data.1973 .

[3] 赵森,钱勇. 自行火炮半自动装填机构输弹问题研究[J].兵工学报,2005，26(5)：592-594.

ZHAO Sen, QIAN Yong. Ammunition ramming of semi-automatic loading device of the self-propelled gun[J].ACTA Armamentarii, 2005，26(5)：592-594. (in Chinese)

[4] 徐灏.机械设计手册(第3卷)[M].北京：机械工业出版社,1991(1)：10-86.

XU Hao.Mechanical design handbook :third volune[M].Beijing:China Machine Press,1991:10-86. (in Chinese)

[5] 陈立平.机械系统动力学分析及ADAMS应用教程[M].北京：清华大学出版社，2005.

CHEN Li-ping.Mechanical system dynamics and ADAMS application tutorial[M].Beijing:Tsinghua University Press,2005. (in Chinese)

[6] 李继科.火炮供输弹系统虚拟样机技术研究[D]. 南京:南京理工大学,2004.

LI Ji-ke. Artillery supply and transport bomb system on virtual prototype technology[D].Nanjing:Nanjing University of Science and Technoloy,2004. (in Chinese)