防空火箭炮无抖振滑模鲁棒控制策略设计

杨 帆，马大为，胡 健

(南京理工大学 机械工程学院，江苏 南京 210094)

随着技术的发展和战略的需要，充当压制性武器的火箭炮现已向防空型武器转变。这就要求在面对比防空高炮更加恶劣的负载特性[1]的同时，防空火箭炮的伺服系统要保证高精度、更快的响应速度以及更强的鲁棒性。

为解决上述问题，多种新兴的控制策略诸如神经网络控制[2]、滑模变结构控制[3]等都被提出并应用在某型号防空火箭炮样机上。其中，滑模控制[1,3-4]以其简单可靠的控制器结构及良好的控制效果在相关领域受到了广泛的关注。如何克服滑模控制特有的输出抖振，以及如何处理好输出控制量与不确定扰动上界的协调问题[5]一直制约着滑模控制的应用与发展，笔者使用自适应的方式获得增益值，推导出一种新型的连续的控制律，有效消除了滑模控制中存在的抖振现象，仿真与实验结果证明该方法是有效的。

1 防空火箭炮系统模型

防空火箭炮系统由方位子系统和俯仰子系统组成，其数学模型一致，参数略有差异。

1.1 系统描述

防空火箭炮系统属于随动设备，接受来自炮位计算机的航路信息θref，通过全炮控制器的计算，输出相应的控制信号(u，即ωref)至各子系统驱动器，驱动器驱动电机(交流永磁同步电机，PMSM)，经过减速器带动转塔和发射箱运动。

1.2 数学模型建立

防空火箭炮以交流永磁同步电机为动力部，驱动转塔与发射箱进行运动。

基于以下假设建立永磁同步电机dq轴数学模型：忽略电动机铁心饱和；不计涡流和磁滞损耗；转子上没有阻尼绕组，永磁体无阻尼作用；相绕组中电动势波形是正弦波；采用Id=0的控制策略[6]。

uq=Riq+Lpt+ωrψf

(1)

ud=-ωrLiq

(2)

Tem=1.5pnψfiq=Ktiq

(3)

Tem=TL+B(ψr/pn)+(J/pn)pωr

(4)

式中：ud、uq、iq与L(L=Ld=Lq)分别为dq坐标系上的电枢电压分量、电枢电流分量和等效电枢电感；R与ωr(=pnωm)分别为电枢绕组电阻和dq坐标系的电角速度；ψf与pn为永久磁铁对应的转子磁链和电机极对数；Tem与TL分别为电磁转矩和负载力矩；B与J分别为阻尼系数和转动惯量；Kt为电磁转矩系数;p为微分算子。

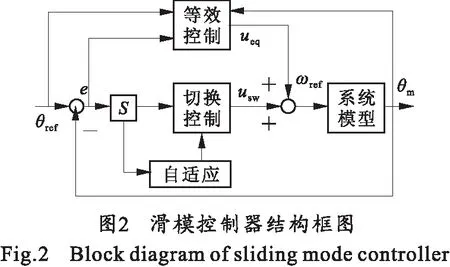
完全解耦控制后的电机带转塔与发射箱的系统框图如图1所示。图中Kj为减速器的减速比，GC为电流环传递函数;K2为速度环比例系数;Kv为速度环反馈系数;ωm为电机实际的速度输出;θm为机构终端检测的角度。

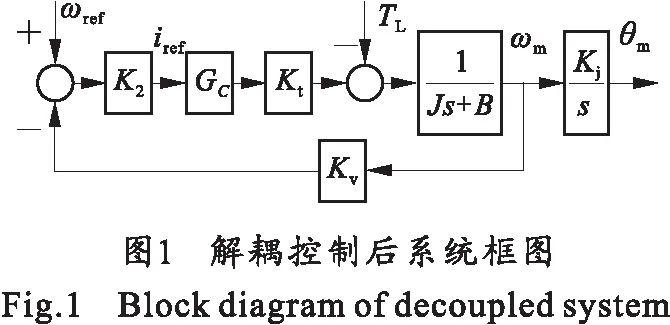
假定电流环完全跟踪[7]，即Gc(s)=1，则有：

θm(s)=G1(s)u(s)+G2(s)TL(s)

(5)

式中：G1(s)=θm(s)/u(s)=K2KtKj/[Js2+(K2KtKv+B)s]；G2(s)=θm(s)/TL(s)=Kj/[Js2+

(K2KtKv+B)s]，整理后有：

(6)

式中：a=-(B+K2KtKv)/J；b=K2KtKj/J；f=KjTL/J。

考虑系统运行时各种扰动及不确定因素，式(6)可写成：

(7)

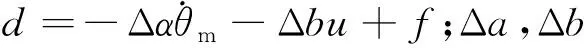
2 鲁棒滑模控制策略设计

选择切换函数：

S=(p+c)n-1e

(8)

式中：c为正常数;e=θref-θm;n=2为系统阶数。

2.1 控制律设计及无抖振优化

式(8)求导得：

(9)

(10)

根据指数趋近律设计的切换控制律形式一般为：usw=b-1(κS+dsgn(S))，其中κ和d为滑模增益，目的为补偿扰动造成的影响。增益选择较小时，无法保证系统的强鲁棒性；而增益选择过大，会造成多余的控制输入，从而造成控制量的抖振。S.C.Y Chung等人提出用Sigmoid连续函数替代法[8]，而孙彪等人提出使用幂次函数替代法[9]，一定程度上抑制了抖振，但经过此种优化方法，连续化后实质上的控制律已经脱离了变结构不连续控制的基础，仍会损害系统的内在鲁棒性。为解决上述问题，本文采用自适应的方法计算增益值，得出切换控制律如式(11)所示：

(11)

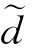
(12)

式中：γ是正常数，取该自适应律能够保证系统半全局镇定。 由式(10)、(11)，控制律u为：

(13)

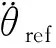
2.2 稳定性证明

将式(7)(13)代入式(9)有：

(14)

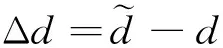
取Lyapunov函数为：

(15)

求导得：

(16)

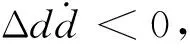
由式(12)的自适应率变化，可得：

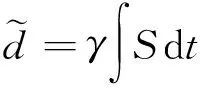
(17)

则式(13)可写成

(18)

将式(7)、(18)代入式(9)，化简得到：

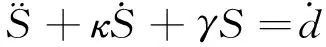
(19)

使用MATLAB的dsolve命令，可解出：

(20)

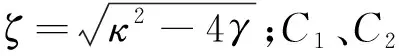
可知，在参数选择适当的情况下，有限时间内S(t)必定会收敛到0。

2.3 微分估计器

本文直接使用文献[10]的成果以获得相关系统的一阶及高阶微分值：

(21)

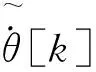
将式(21)表示的两个估计器串联，便能近似获得位置信号的二阶微分。

3 系统仿真与实验

防空火箭炮系统设计指标为：最大调转速度50°/s，最大角加速度70°/s2。定位误差不大于1 mil，动态跟踪误差不大于4 mil。

3.1 系统参数

系统参数为：电机功率3 600 W，电机最高转速2 500 r/min，最大电流12.8A，额定电流6.4A，减速比1∶231，不平衡力矩和摩擦力矩折算为4.86 N·m，满载惯量折算为J=0.002 627 kg·m2，B=0.000 143 N·m·s，Kt=1.11 N·m/A，Kj=1∶231，Kv=0.031 8。控制器参数为：c=5.8；κ=900；γ=11 000。控制器输出信号为u∈[-10V,10V]，对应转速为[-2 400 r/min, 2 400 r/min]。对比组PID位置控制器参数为：Kp=20，Kd=0.24。

3.2 仿真与分析

给定未来点信息为：0 s时刻，阶跃θref=20°，1 s时刻起每隔0.2 s在电机轴上施加15 N·m、持续时间为0.02 s的冲击力矩，模拟火箭炮发射时的燃气流冲击力矩。其阶跃响应如图4所示,图4中1表示采用无抖振滑模控制下的曲线，2表示采用采用传统PID控制下的曲线；滑模控制输入量u如图5所示。

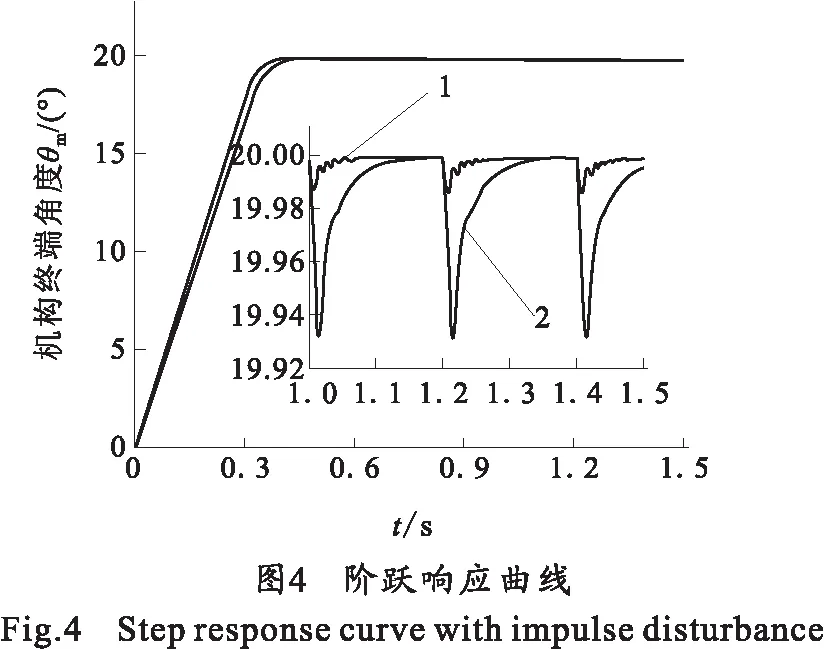
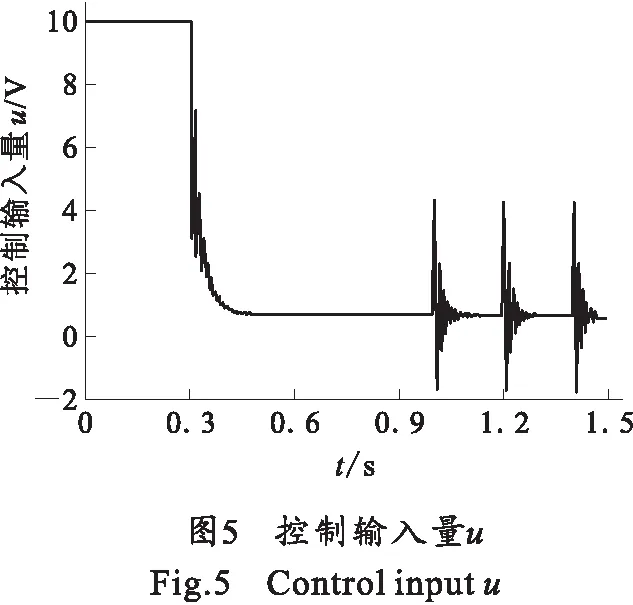
图4中可看出，采用文中所述控制策略时，系统阶跃响应时间略快于采用传统PID控制，而其鲁棒性更强，受到冲击力矩时位置偏移量更小。图5中控制输入平滑，冲击力矩造成的影响被抵消。

3.3 实验论证

实验条件为：电机功率3 600 W，最高转速2 400 rad/min，最大电流12.8 A，额定电流6.4 A，最大输出转矩25 N·m。位置反馈在减速器的输出端，速度反馈在电机轴输出端。以AVR单片机系统作为信号发生器，产生航路信号如下：幅值10°，周期为5 s的方波，跟踪曲线如图6所示；正弦20°sin(лt)，跟踪误差曲线如图7所示。

实验曲线中可看出，采用优化后的无抖振滑模算法，动态跟踪时误差最大为0.12°，均方差为0.058 7°(<4mil)，满足指标要求。

4 结 论

本文以某型号防空火箭炮为被控对象，针对滑模控制输入存在抖振的问题，设计了一种基于自适应增益的无抖振滑模鲁棒控制策略。提出通过计算增益值，并将其作为鲁棒项直接写入控制器中，避免了传统滑模控制中过高的切换增益以及不连续的开关函数带来的控制量的抖振。控制器需要的所有参数都能通过直接测量或者微分估计器给出，避免了高阶系统中高阶微分信号的畸变或不可测问题。仿真与实验验证了该鲁棒控制策略的效果。

[1] 朱玉川. 某箱式多管火箭炮快速装填与高精度自动操瞄系统研究[D]. 南京:南京理工大学，2007.

ZHU Yu-chuan. Research on rapid loading and high precision automatic operating & aiming system of a certain canister multiple rocket launcher[D]. Nanjing: Nanjing University of Science and Technology, 2007. (in Chinese)

[2] 柴华伟，李志刚，马大为. CMAC与PID的并行控制在火箭炮交流伺服系统中的应用[J]. 火炮发射与控制学报，2006(3)：19-22.

CHAI Hua-wei, LI Zhi-gang, MA Da-wei. Application of compound control based on CMAC and PID in AC servo system for rocket launcher[J]. Journal of Gun Launch & Control, 2006(3): 19-22. (in Chinese)

[3] 朱玉川，马大为，李志刚. 火箭炮交流位置伺服系统滑模变结构控制策略[J]. 火炮发射与控制学报，2007(2)：11-25.

ZHU Yu-chuan, MA Da-wei, LI Zhi-gang, et al. Sliding mode variable structure control strategy of AC position servo system of MLRS[J]. Journal of Gun Launch & Control, 2007(2): 11-25. (in Chinese)

[4] FU Tian-Jun, XIE Wen-Fang. A novel sliding-mode control of induction motor using space vector modulation technique[J]. ISA Transactions, 2005(44): 481-490.

[5] GIORGIO BARTOLINI, ALESSANDRO PISANO, ELIO USAI. On the second-order sliding mode control of nonlinear systems with uncertain control direction[J]. Automatica, 2009(45)：2982-2985.

[6] GUO Ya-jun, MA Da-wie, LE Gui-gao. Backstepping and sliding mode cascaded compound control for AC position servo system[C]. PrimeAsia, Shanghai, 2009: 145-148.

[7] 郭新华，温旭辉，赵峰，等. 基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器[J]. 中国电机工程学报，2010，30(27)：7-13.

GUO Xin-hua, WEN Xu-hui, ZHAO Feng, et al. A novel IP speed controller of PMSM based on electromagnet torque feedback compensation[J]. Proceedings of the CSEE, 2010, 30(27): 7-13. (in Chinese)

[8] CHUANG S C Y, LIN C L. A transformed Lure problem for sliding control and chattering reduction[J]. IEEE Transactions on Automatic Control(S0018-9286), 1999, 44(3): 563-568.

[9] 孙彪, 孙秀霞. 一种新的趋近律离散滑模控制方法及仿真[J]. 系统仿真学报, 2010, 22(10):2422-2425.

SUN Biao, SUN Xiu-xia. New algorithm of reaching-law discrete-time sliding mode control and simulation[J]. Journal of System Simulation, 2010, 22(10): 2422-2425.(in Chinese)

[10] 田大鹏，吴云洁，刘晓东. 高精度电机伺服系统控制综合方法[J]. 电机与控制学报，2010, 14(7)：66-74.

TIAN Da-peng, WU Yun-jie, LIU Xiao-dong. Synthesis methods of high precision motor servo system control[J]. Electric Machines and Control, 2010, 14(7)：66-74. (in Chinese)