基于GM(1，1)数据融合算法的滑坡预测研究

王腾军，赖百炼，叶俊华，杨志强

(1.长安大学地质工程与测绘学院，陕西西安710054;2.中国煤炭地质总局航测遥感局，陕西西安710054)

基于GM(1，1)数据融合算法的滑坡预测研究

王腾军1，赖百炼2，叶俊华1，杨志强1

(1.长安大学地质工程与测绘学院，陕西西安710054;2.中国煤炭地质总局航测遥感局，陕西西安710054)

滑坡会对人类生命和财产造成巨大损失，预测预报是预知滑坡灾害发生并减少其影响的重要手段。GM(1，1)算法在滑坡预测中得到普遍应用，该算法具有较少数据量建模的优点。对于滑坡不需要了解各种影响因子的具体状态，但存在建模数据量选取不确定性和长时距预测精度降低的问题，以GM(1，1)模型为基础，引用数据融合技术，对滑坡变形量进行预测，并用实测数据进行验算，结果表明该方法能提高滑坡的预测精度。

GM(1，1);数据融合;滑坡变形;变形预测

一、引 言

滑坡作为一种自然地质灾害，常常会造成巨大的生命财产损失，已成为仅次于地震的第二大自然灾害。为了预防灾害的发生，很有必要事先对滑坡发生的时间做出预测预报。经过国内外许多专家学者的几十年的潜心研究、探索，提出了多种滑坡预测预报的理论模型和方法［1］，可概括为以下4种:确定性预测预报模型;统计预报模型;非线性预报模型;宏观预报模型。在统计预测预报模型中，代表性的有灰色GM(1，1)模型、回归分析法、指数平滑法等多种方法。

GM(1，1)模型数据需求量低，一般几个数据就可以建立模型，直接从所面对的数据中提取信息，其适用于中短期和临滑预测预报［1］。对于GM(1，1)模型进行中长期预测预报精度较差的问题，可以通过实测值迭代和数据融合技术加以改化，数据融合(data fusion)是利用计算机技术将来自多个传感器或多源的观测信息进行分析、综合处理，从而得出决策和估计任务所需的信息的处理过程，它往往能获取比单一数据更加可靠的结果［2-3］。

由于GM(1，1)模型长期预测的有效性明显受到系统时间序列长短及数据变化的影响，因此如果系统建模运用数据列太短，则难以建立长期的预测模型;数据列过长，系统干扰的成分太多，不稳定因素大，易使模型精度降低［4］。针对选取多少数据建立模型，文中所采取的方法是迭代入实测值后构成等维灰色递补动态预测，在递补数据基础之上选择不同量的数据序列建立多个预测模型，而后对不同模型的预测结果进行数据融合，以获取更加准确的预测值。

二、GM(1，1)基本模型［5-6］

若假设 x(0)(k)为测量的滑坡位移值，由x(0)(k)构成的非负序列X(0)为

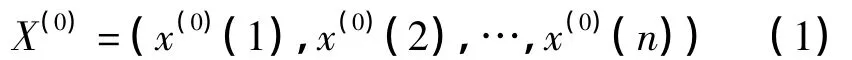
式中，x(0)(k)≥0，k=1，2，…，n。

设X(1)为X(0)的一阶累加生成序列

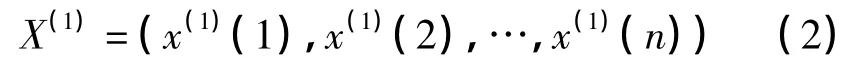
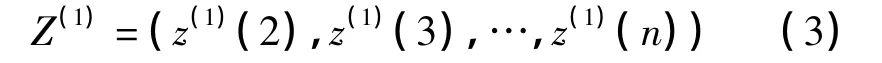
式中，z(1)(k)=0.5(x(1)(k)+x(1)(k－1))，(k=2，3，…，n)。

若 ^Α=［a b］Τ为参数列，且

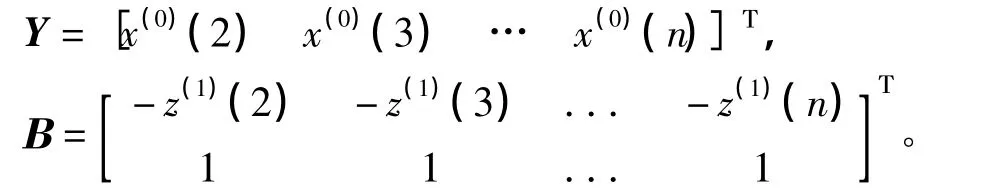
则GM(1，1)模型

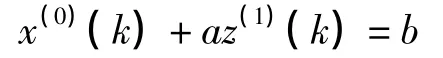
的最小二乘估计参数列满足

那么GM(1，1)模型的白化方程为

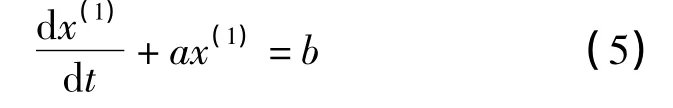
由白化方程得到时间响应函数

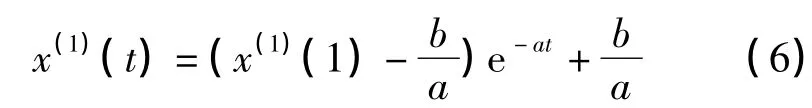
可以得到GM(1，1)模型x(0)(k)+az(1)(k)=b的时间响应序列为

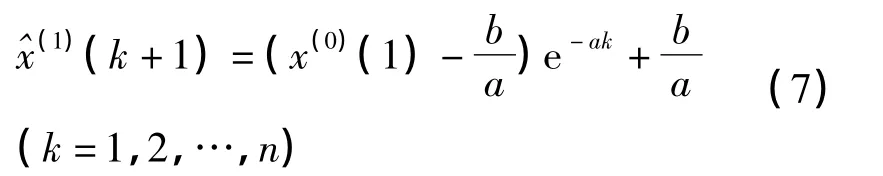
那么还原值为

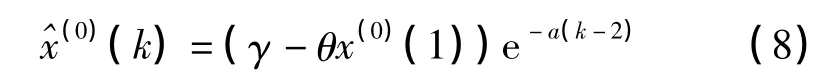
三、GM(1，1)数据融合预测算法

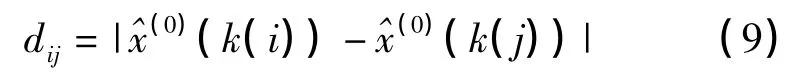
式中，i，j∈{1，2，…，m}。

构造两个数据间的支持度函数rij，其必须满足以下两个条件。

1)rij与相对距离成反比关系，即两个值相差越大，彼此之间支持程度越小。

2)rij∈［0，1］，使数据的处理能够利用模糊集合理论中隶属函数的优点，避免数据之间相互支持程度的绝对化。

rij的选取可以由很多种，以下为最简单的两种形式［7］。

阶跃型

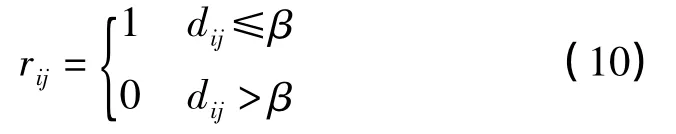
式中，β为常数。

分段型

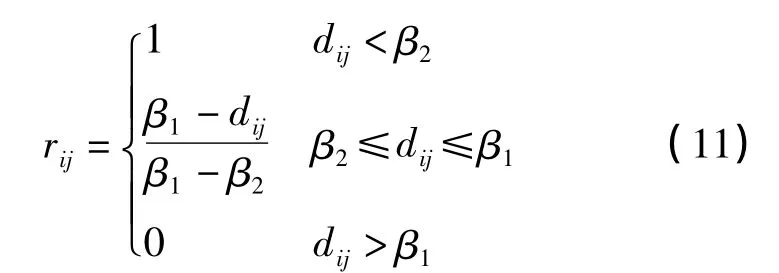
式中，β1、β2为常数，且β2＜β1。

如下为几种常见的支持度函数［7-8］

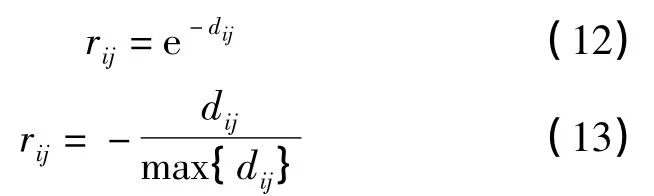
式中，i，j∈{1，2，…，m}。

选择式(13)建立如下支持度矩阵

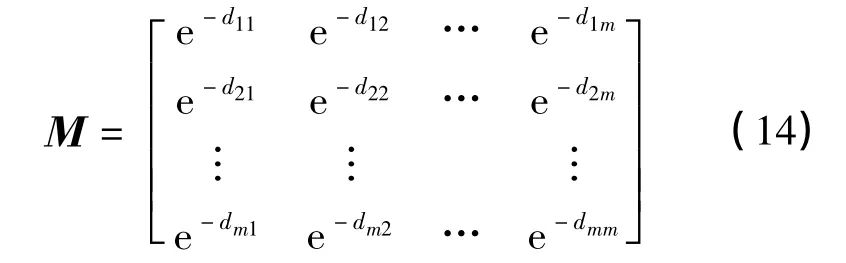
即

其矩阵形式为

式中，Η、Ν分别为由ωi和vj组成的列向量;Μ为非负对称矩阵，存在最大模特征值λ;与其对应的特征向量为］，量全为非负数。由特征向量特征值性质，可以取

融合后可以得到的预测值为

残差为

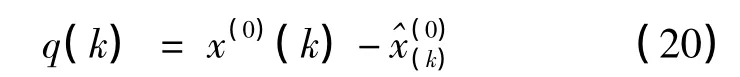
其相对误差为

四、实例验算

本文实例选用某滑坡沉降监测点1号点的位移时间序列数据［9］进行验算。1～30期位移数据用于建模，31～48期位移数据进行预测计算，并与实测值比对，对预测结果进行精度评定，其结果如表1、图1所示。

五、结 论

通过利用GM(1，1)预测模型并引用数据融合理论得到GM(1，1)数据融合预测算法，最后结合滑坡实例验算，得出如下几点结论。

1)由图1可以看出，利用GM(1，1)模型作滑坡位移预测，由于自身误差的不断积累，导致长时距的预测结果越来越偏离实际;利用实际测量值不断的迭代，对模型进行等维重建，可以促使模型不断的自我修正;而后将不同维数时序数据建立的几个GM(1，1)模型的预测值利用GM(1，1)数据融合算法进行预测值融合，就可以得到相对更好的结果，提高了预测精度。

2)表1中得到的GM(1，1)数据融合预测值是通过选取不等维的时序数据构造4个GM(1，1)模型，最后融合得到的预测值。在本文实例验算中，笔者通过试验发现构造4个GM(1，1)模型进行融合就可取得最优效果。对于其他滑坡的时间序列数据，构造多少个不等维GM(1，1)模型进行数据融合可以精度达到最高尚需进一步研究。

3)由图1中时序38对应的预测数据可以看出，GM(1，1)数据融合预测模型的预测值偏差较大，预测的精度较低，对于某些突变的预测可能失效，尚需对模型进一步研究。

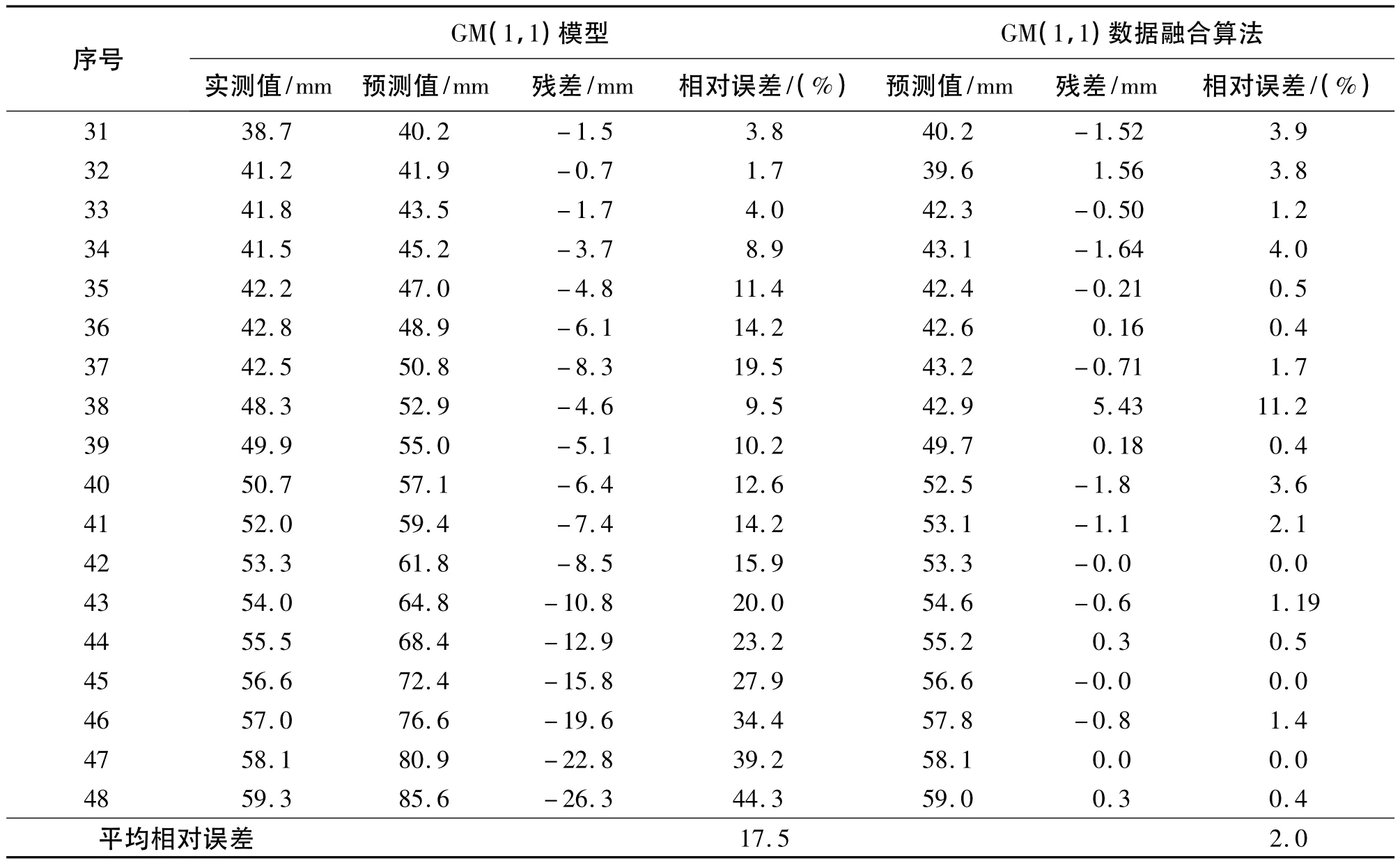
表1 GM(1，1)模型预测值与GM(1，1)数据融合模型预测值对比表

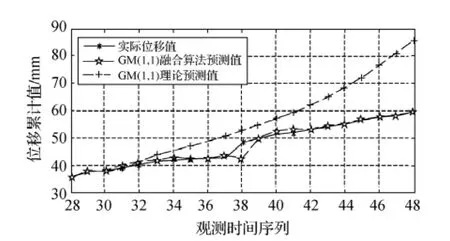
图1 利用实测值迭代的融合结果与GM(1，1)理论预测值比对图

［1］ 李秀珍，许强.滑坡预报模型和预报判据［J］.灾害学，2003，18(4):71-78.

［2］ 张华伟.数据融合算法研究及DSP实现［J］.武汉理工大学学报，2009，31(3):84-86.

［3］ 焦明连，蒋廷臣.基于GPS-InSAR集成技术地表形变的监测［J］.测绘科学，2008，33(6):57-59.

［4］ 尹晖.时空变形分析与预报的理论和方法［M］.北京:测绘出版社，2002.

［5］ 邓聚龙.灰预测与灰决策［M］.武汉:华中科技大学出版社，2000.

［6］ 刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.3版.北京:科学出版社，2004.

［7］ 高方伟，刘贵喜，王蕾，等.基于支持度矩阵的一种多传感器融合方法［J］.弹箭与制导学报，2007，27(4): 284-287.

［8］ 胡振涛，刘先省.一种实用的数据融合算法［J］.自动化仪表，2005，26(8):7-9.

［9］ 张军，刘祖强，邓小川，等.滑坡监测分析预报的非线性理论和方法［M］.北京:中国水利水电出版社，2010.

Research on Landslide Prediction Based on GM(1，1)Data Fusion Algorithm

WANG Tengjun，LAI Bailian，YE Junhua，YANG Zhiqiang

0494-0911(2012)05-0063-03

TU459

B

2012-03-09

王腾军(1967—)，男，河南淮阳人，副教授，主要研究方向为变形监测及预测预警。