连分式与曲线拟合模型在沉降监测中的应用研究

赵 言，花向红，尹志永

(1.武汉大学测绘学院，湖北武汉430079;2.天津测绘院，

天津300381;3.武汉大学灾害监测与防治研究中心，湖北武汉430079)

连分式与曲线拟合模型在沉降监测中的应用研究

赵 言1，2，花向红1，3，尹志永2

(1.武汉大学测绘学院，湖北武汉430079;2.天津测绘院，

天津300381;3.武汉大学灾害监测与防治研究中心，湖北武汉430079)

分析沉降监测数据的特点，采用连分式和曲线拟合模型对建筑物沉降监测数据进行处理，实现两种数据处理模型的建模过程并进行对比分析。最后将模型用于建筑物沉降量的实际预测，验证模型的可行性及实用性。

连分式;曲线拟合模型;建筑物沉降;变形预报

一、引 言

随着现代数据处理技术方法的不断进步，可应用于建筑物沉降监测数据处理的模型与方法有很多，如自回归分析法、灰色关联分析法、神经网络法等，但这些方法对沉降监测数据都有一定的建模要求，如果条件不符或达不到，则会出现建模错误，或在预报分析中产生较大的误差。针对这种情况，通过分析建筑物沉降监测数据的特点，将连分式法和曲线拟合法引入建筑物沉降监测数据处理中。通过对武汉市某小区楼房建筑物沉降监测数据进行计算、分析，比对两种方法处理实测数据的结果，验证其可行性与实用性。

二、连分式拟合模型

设已知监测数据拟合函数f(x)在某一监测点n+1期的变化量为yk=f(xk)(k=0，1，…，n)，构造函数连分式

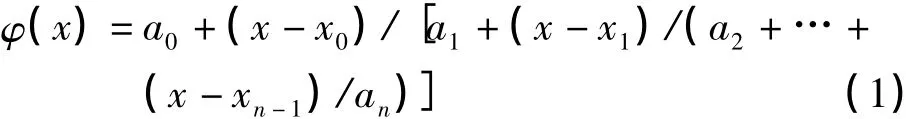
使得

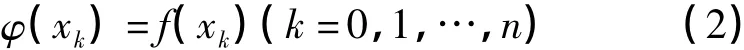
构造连分式拟合函数如式(1)，实际上就是根据监测对象周期和监测对象形体变化量n+1期的数据所要满足式(2)的条件，确定式(1)中的参数a0，a1，…，an，进一步建立连分式拟合模型方程。

根据数学公式变换，将式(1)经过整理得到有理分式，因此，连分式插值(拟合)又称有理插值。但在实际应用中，连分式这种形式运算比较方便，而且不存在误差累计的问题，所以一般不把连分式化为有理分式。

为了确定式(1)中的各参数 a0，a1，…，an，将式(1)进行逐节分解，即有

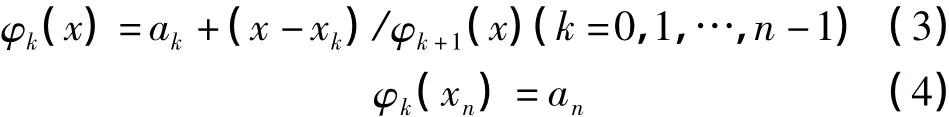
由式(3)可以看出

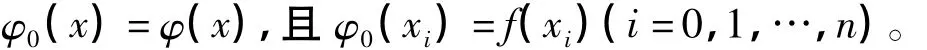
由式(3)和式(4)，可得

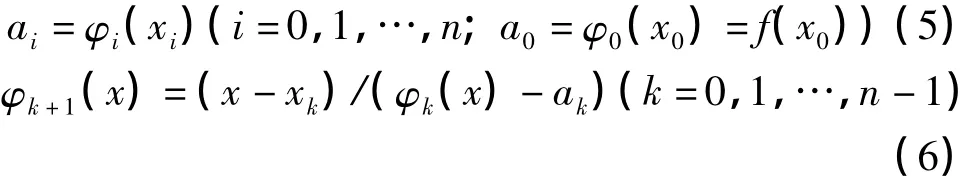
由式(6)可以计算得到ai=φi(xi)(i=0，1，…，n)的递推公式

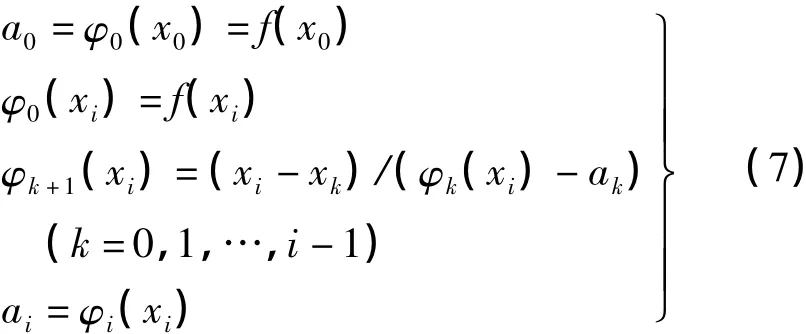
根据式(7)可以计算出ai=φi(xi)(i=0，1，…，n)的格式系数。

对连分式模型精度(即模型拟合程度)评定的方法有残差大小检验、关联度检验和后验差检验3种，本文采用后验差方法检验连分式模型的精度(具体详见参考文献［2］)。

三、曲线拟合预测模型

曲线拟合通常也称离散数据的曲线拟合，指的是从给定函数y=u(t)的一组观测值(ti，yi)(i=0，1，…，m)选定一组简单函数φk(t)(k=0，1，…，n)作为基函数，通过确定方程 f(t)=x1φ1(t)+ x2φ2(t)+…+xnφn(t)指定的参数xk，使f(t)与观测值(ti，yi)在总体上尽可能接近，即得到一个最佳的函数f(ti)来逼近yi。

在建筑物沉降监测数据建模时，假设某建筑物监测点的高程为y，其中y是随观测时间(或观测周期)x变化而变化的函数。假设y=a0+a1x+a2x2+…+amxm，令

式中，m为拟合多项式次数;n为特征点重复观测次数。

根据最小二乘原理，可得

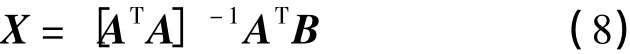
将通过式(8)求得的模型系数代入拟合方程，即得到曲线拟合模型。但建立的曲线拟合模型是否与实际变形规律相符合，需要对预测方程进行假设检验。

如果建立的曲线拟合模型与建筑物形体变化规律相符合，那么曲线拟合方程的系数:ak≠0(k= 0，1，…，n)，否则ak=0(k=0，1，…，n)。于是可作检验假设:H0:ai=0，H1:ai≠0。根据F分布的定义，检验公式如下

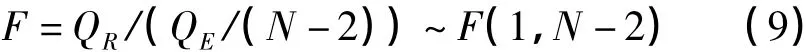
给定显著水平α，当式(9)中的F＞Fα(1，n－2)时，则拒绝H0，接受H1，认为形变量y(t)线性依赖于时间变量φ(t)，即存在线性关系，所建立的曲线拟合模型有效;否则，认为所建立的曲线拟合模型无效。

四、实例分析

根据以上连分式和曲线拟合模型建模原理，笔者利用对武汉市某小区建筑物一个沉降监测点监测获取的监测数据，取其中连续的33期进行建模分析(前30期用于建模，后3期用于监测模型预测效果评价)，通过获取距离拟合(预测)周期最近的10期数据(即建立该连分式模型至少需要10期监测数据)，建立连分式拟合模型，并对用于建模的前30期监测数据进行拟合，同时预测后3期(第31、32、33期)数据，得到结果如表1所示。表1中，T为观测周期;Δh为沉降监测值;Δh'为连分式拟合模型拟合值;ΔC1、ΔC2、ΔC3分别为二次、三次、四次曲线拟合模型拟合值。

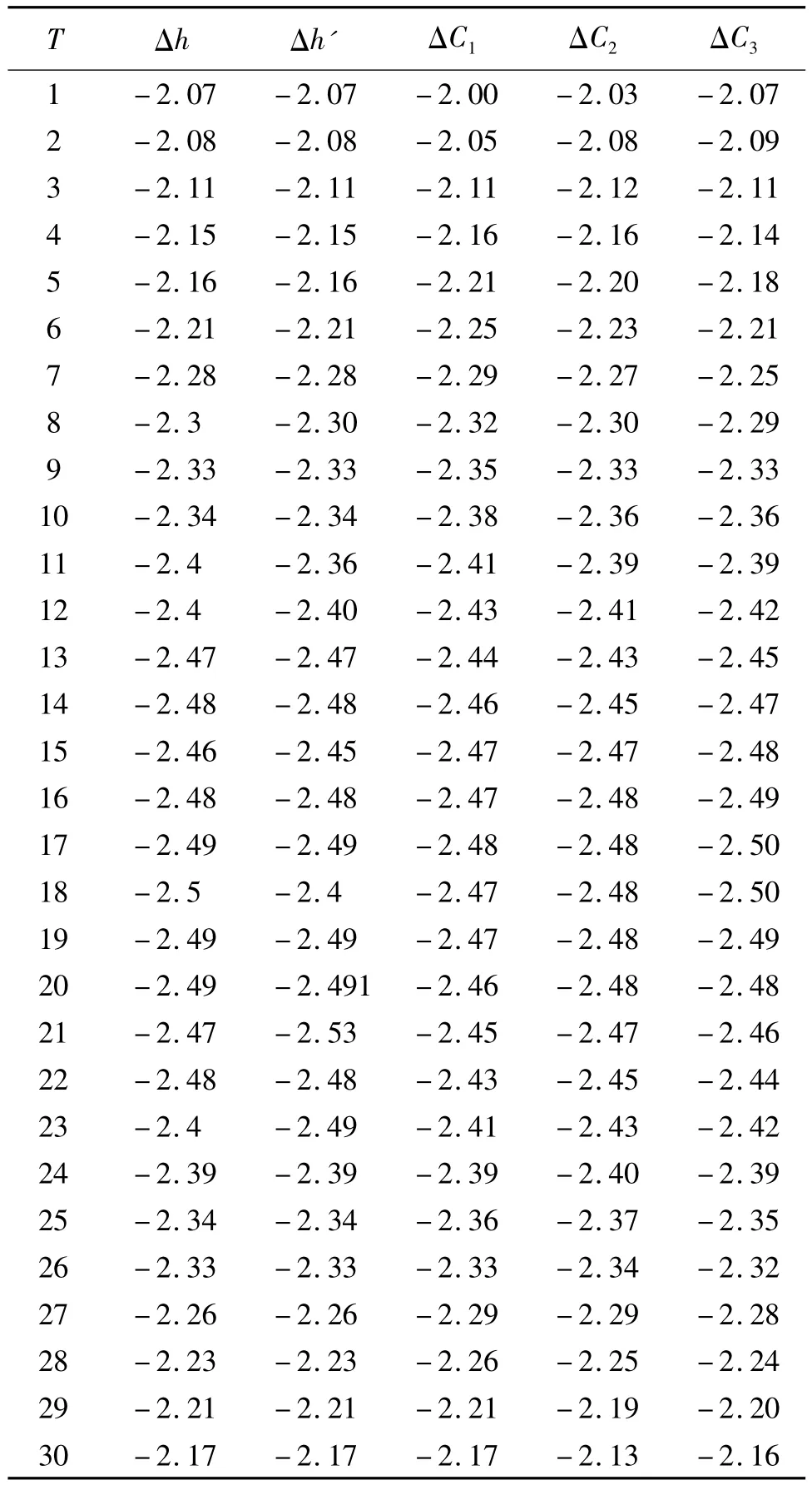
表1 沉降监测值与模型拟合值 cm

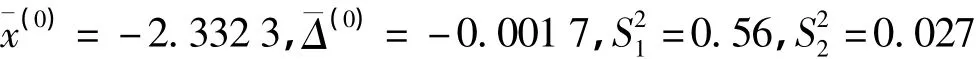
可求得后验差比值:C=S2/S1=0.219，小误差概率:P={|Δ(k)|＜0.674 5S1}=1，即连分式模型拟合值与监测值的差值全部小于0.067 45S1，根据后验差法精度判定标准，可判定C=0.219＜0.35，且P=1＞0.95，模型等级精度为1级(好)，因此，所建立的连分式拟合模型可以用来处理沉降监测数据，且模型拟合精度很高(具体如图1所示)。

对曲线拟合模型，根据表1中的数据，可以求出四阶曲线拟合模型的中误差为±0.08，拟合效果最好，因此，选择四阶曲线拟合模型为预测模型。由f检验可知，因线性关系引起的偏差平方和 QR= 0.553 6，因除线性关系之外的其他因素引起的偏差平方和QE=0.08，经计算，取显著水平α为0.05时，F=193.76，Fa(1，28)=4.20，F＞Fa(1，28)，模型显著。因此，根据实测沉降数据建立的曲线拟合模型也能较好地反映建筑物实际的沉降变化情况，同样也具备较高的拟合精度(具体如图1所示)。

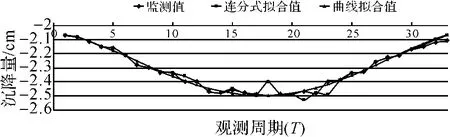
图1 模型拟合预测值与监测值比较

根据建立的连分式拟合模型和四阶曲线拟合模型，对未来3期数据(第31、32、33期)小区建筑物的沉降值进行预测，如表2所示。表中，T为观测周期，Δh为沉降监测值，Δh'为连分式拟合模型预测值，ΔC3为四阶曲线拟合模型预测值)

表2 模型预测值与实测值对比 cm

从表2模型预测值与实测值的对比可以看出，连分式拟合模型和四阶曲线拟合模型在短周期预报时具有较高的预测精度，随着预报周期次数的增加，预报精度逐渐降低。对比连分式拟合模型与四阶曲线拟合模型预测值与实测值差值的大小，虽然连分式拟合模型在拟合建模数据过程中有个别值相对于四阶曲线拟合模型相差较大，但在预测未来周期沉降变化量的效果要比四阶曲线拟合模型预测的效果好。

五、结束语

通过对连分式与曲线拟合模型的研究，分别将其应用到实际的沉降监测数据处理中，根据模型建模原理实现了两种模型的建模过程，并对具体监测形体的沉降值进行了预报分析。经过对拟合预测结果的分析、对比，得出这两种数据处理方法都能达到预期的精度要求，以及连分式拟合模型的预测精度要比最优阶次曲线拟合模型的预测精度稍好的结论。值得一提的是，在建筑物突然发生大幅度的形体沉降变化时，这两种预报模型的预测精度不再能够得到保证，主要是因为连分式和曲线拟合模型都是建立在连续变化的监测数据基础上的线性模型，对建筑物突变性沉降的预测能力较低。因此，若要在有突变性变化的情况下仍然取得较高的预测精度，需增加相应的参数变量。

［1］ 徐士良.数值分析与算法［M］.北京:机械工业出版社，2007.

［2］ 黄声享，尹晖，蒋征.变形监测数据处理［M］.武汉:武汉大学出版社，2007.

［3］ 李强.关于连分式中几个问题的研究［D］.合肥:合肥工业大学，2009.

［4］ 汤仲安.矢量GIS平面一般曲线等概率密度误差模型的几何特征［J］.测绘学报，2007，36(1):91-95.

［5］ 金彪，吴北平，李艳芳.曲线拟合与自回归模型在地铁变形监测中的运用［J］.地矿测绘，2009，25(1):35-37.

［6］ 肖萍.连分式渐近式的一个递推算法及其应用［J］.中南工业大学学报，2002，33(5):547-549.

Application of Continued Fraction and Curve Fitting Model to Subsidence Monitoring

ZHAO Yan，HUA Xianghong，YIN Zhiyong

0494-0911(2012)06-0019-03

P258

B

2011-06-01

国家自然科学基金项目(41174010;41074025)

赵 言(1988—)，男，安徽亳州人，硕士生，主要研究方向为精密工程测量与工程变形监测。