预应力连续箱梁桥的动力有限元模型修正

林贤坤，张令弥，郭勤涛，覃柏英

（1.广西工学院a.广西汽车零部件与整车技术重点实验室；b.理学院，广西 柳州 545006；2.南京航空航天大学a.振动工程研究所；b.机电学院 南京 210016）

在《不中断交通的梁式桥梁试验及状态评定方法的研究》这一项目的研究过程中，以桥梁承载力的快速评定为目标，项目组提出了基于运行模态分析的模态挠度法[1]。该方法应用于桥梁承载力评定时，首先需对试验模态振型质量归一化。为此项目组提出了基于有限元模型的质量归一化法。因此，为了模态挠度法有效和可靠应用于桥梁承载力评定，需建立桥梁较精确的有限元模型。

预应力混凝土连续梁桥，具有结构刚度大、变形小、整体性能和抗震性能好，特别是主梁变形挠曲线平缓，桥面伸缩缝少，行车舒适等优点，在桥梁工程中得到广泛采用。针对该类桥型的健康检测、状态评估与维修加固等任务，若能建立基本准确反映其实际动力行为的有限元模型，无疑具有重要意义。然而，对于桥梁有限元模型，其建模过程中会引入各种假设和简化，同时存在诸多不确定因素，都会导致与真实模型间存在误差，因此，须对它进行修正。

模型修正对象常分为结构的质量阵与刚度阵、物理和几何等设计参数，后者的物理意义明确，更具工程应用价值。频率、振型、反共振频率和振型相关系数等模态数据常用于模型修正。根据问题的需要，许多研究者[2－7]采用了不同的模态数据。目前对于模型修正的方法，主要有基于统计分析技术[8]、灵敏度分析[9]、微粒群算法[10]、神经网络[11]和遗传算法[12]等优化算法。遗传算法，作为一种高度并行、随机和自适应搜索算法，特别适用于有限元模型修正这类复杂非线性优化问题。

本文以张家港河大桥为对象，构造有限元模型的2个评价指标：频率和振型相关系数，由此定义目标函数，采用该桥环境激励模态试验的结果，基于实数编码加速遗传算法对有限元模型进行修正，并对修正后有限元模型的预测能力进行评估，由此探讨预应力连续箱梁桥的动力有限元模型修正问题。

1 张家港河大桥简介

张家港河大桥，位于江苏省江阴市新陆长路跨越通航河流张家港，其主桥采用（49＋82＋49）m三跨变截面预应力混凝土连续箱梁，主桥与两副桥间设置有伸缩缝。其总体图如图1所示。

图1 张家港河大桥主桥的总体图

2 模态试验

2009年4月，对张家港河大桥主桥实施了环境激励的模态试验。在桥面内外侧分别布置14个可移动的竖向测点和1个固定的竖向参考点。前者用⊕、⊗和⊖标注，后者用⊙标注，如图2所示。试验分4组进行，每组包括7个移动测点和2个参考点，共9个通道。数据采集设备包括江苏联能电子的动态采集系统（YE6268）和中国地震局工程力学研究所的加速度传感器（891－2）等，现场采样频率为50Hz，采样时间为30min。

图2 模态试验中传感器的位置

由于环境激励的模态试验无法测量输入，因此，采用运行模态分析法（Operational Modal Analysis，OMA）[13－14]，对测试结果进行模态参数识别，获得张家港河大桥主桥的10阶试验模态参数，结果如表1所示，振型如图3所示。

3 初始有限元模型的建立

采用软件MSC.Patran，根据设计图纸，建立张家港河大桥的初始有限元模型，节点和单元总数分别为7952和7282个，其中Bar2梁单元148个，Quad4单元5874个，Tria3单元28个，Hex8体单元1232个，MPC单元100个，如图4所示。

4 有限元模型的修正

建模过程中，较多理想化假定与简化的采用，以及诸多不确定因素的存在，导致初始有限元模型往往难以与实际模型较好吻合，因此，须根据桥梁原型的试验结果修正其初始有限元模型。

4.1 待修正参数

导致初始有限元模型与实际模型不相符的因素很多，因施工和环境变化等原因引起几何和材料参数与设计值不符而成为主要因素。对于腹板和底板的宽度与厚度，支座的几何尺寸可较精确地获得，因而无需修正。因沥青层、水泥砼调平层和锚头处简化并入桥梁主体，引起顶板的厚度与设计值有出入，将作为待修正参数。根据工程经验，桥梁的实际材料参数常与设计值存在差异，因此，各梁段的材料参数将作为待修正参数。同时，由于与支座连接的边界条件、主桥墩高度的取值、护栏的几何与材料参数对动态特性都有影响，也都将作为待修正参数。

表1 模态试验的识别结果

图3 张家港河大桥的10阶试验模态振型

图4 张家港河大桥主桥的有限元模型

4.2 评价指标

在修正过程上，为了评价有限元模型，利用计算与试验的模态参数，定义如下的2个评价指标。

4.2.1 频率指标 设第m阶试验频率为fEm，与其相匹配的计算频率为fAm（x），m＝1，2，…，M。其中x为有限元模型的设计参数。则频率指标定义为两者的相对误差rm（x），Rm（x）和其标准差s（x）[15]：

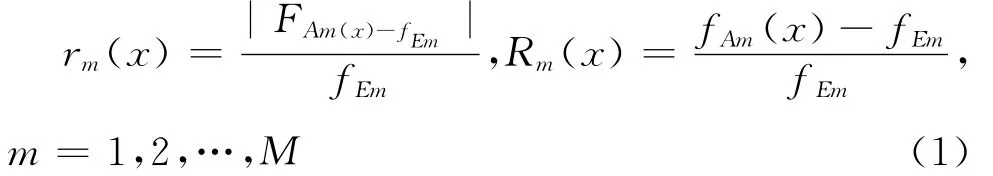
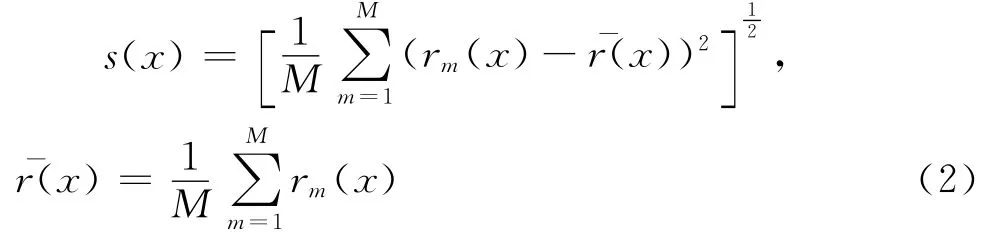
因此，频率指标越接近0，设计参数对应的有限元模型的计算频率越接近实桥的试验频率。

4.2.2 振型相关系数指标 设第m阶试验振型为φEm，与其相匹配的初始和设计参数x对应的有限元模型的计算振型分别为φIm和φUm（x），φIm、φUm（x）与φEm的振型相关系数分别为 macIm、macUm（x），m＝1，2，…，M。由此可定义振型相关系数指标[15]：

em（x）反映了 macUm（x）相对于 macIm的提高，m＝1，2，…，M，但em（x）与初始有限元模型有关。为了避免其影响，可定义另一振型相关系数指标（x）[15]：

因此，em（x）与初始和修正有限元模型都有关，（x）只与修正有限元模型有关，且em（x）的值越大，或（x）的值越小，修正有限元模型的计算振型越相似于试验振型。

4.3 模型修正的数学模型

设对应的有限元模型的特征量为fA（x），相应的试验结果为fE，其中fA（x）是频率、振型、反共振频率、振型相关系数，或者它们的组合。对于有限元模型修正问题，目标是寻求设计参数，使fA（x）与fE间达到最佳。因此，基于fA（x）和fE的有限元模型修正问题可描述为式（5）所示的优化问题[15]。

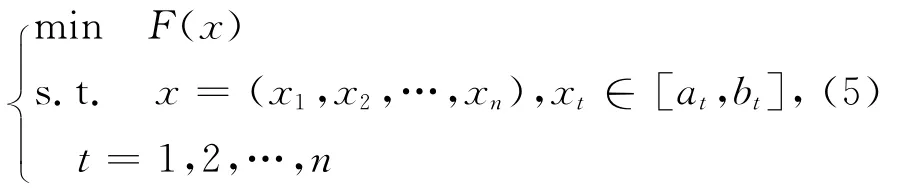
其中F（x）是由fA（x）和fE确定的最小化目标函数。

因此基于fm（x），s（x）和em（x）或的有限元模型修正问题可转化为式（6）、（7）所示多目标优化问题[15]。

或

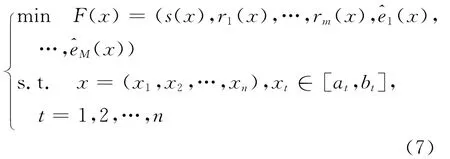
其中 F（x）是关于s（x），rm（x）和em（x）或（x）（m＝1，2，…，M）的最小化目标向量。

4.4 目标函数

对于式（6）和（7）的多目标优化问题，其各目标函数间常互相矛盾，很难找到一个解，使所有目标函数同时达到最小。结合本文的实际问题与目标加权法，由rm（x），s（x）和em（x）可定义式（6）所示的目标函数[15]：

也可由rm（x），s（x）和em（x）定义式（7）所示的目标函数[15]：

其中μ，βm，γm为权重，代表其子目标函数s（x），rm（x），em（x）或（x）在目标函数中的重要程度。s（x）能较好控制各rm（x）的差异程度；μβm，γm的取值，能控制各rm（x）和em（x）或（x）对目标函数值的影响。目标函数值F1（x），F2（x）越小，有限元模型越准确反映桥梁的真实动态特性。

针对张家港河大桥的有限元模型，目标函数F1（x），F2（x）中μ，βm的取值都为：μ＝7和rm（x）＞6.0时，βm＝2.0，否则βm＝1。但对于γm的取值，F1（x）中 macUm（x）＞ 0.80时，γm＝0.5，否则γm＝1；F2（x）中 macUm（x）＜0.80时，γm＝2.0，否则γm＝1，m ＝1，2，…，M。

由表3的评价结果可知，式（8）和（9）定义的目标函数和权重的取值是合理的。因此，权重取相应值后，基于目标函数或，由前7阶试验模态参数，可利用实数编码加速遗传算法修正初始有限元模型。

4.5 实数编码加速遗传算法

对于实数编码加速遗传算法，现介绍其应用于有限元模型修正问题式（6）和（7）的主要运算步骤，其流程图如图5所示[15]。

表2 4个有限元模型的分析结果

表3 4个有限元模型的评价结果

图5 实数编码加速遗传算法的流程图

1）个体的编码与解码 基于实数编码对设计参数，采用线性变换

则可把第t个设计参数xt映射为实数yt，其中xt∈ [at，bt]，yt∈ [0，1]。把yt（t＝1，2，…，n）顺次连在一起，可构成设计参数向量x＝ （x1，x2，…，xn）对应的个体 （y1，y2，…，yn）。反之根据式（10），由个体 （y1，y2，…，yn）可获得对应的设计参数向量x＝（x1，x2，…，xn）。

2）个体评价的方法 遗传算法仅利用评价函数评估解群的优劣，因此，选取评价函数至关重要，直接影响到算法的收敛速度及能最优解寻找。评价函数给定的各个体的评价值，用于确定该个体被选择的可能性。评价值越高，被选择可能性越大。为了使评价值不受实际目标值影响，定义第i个个体的评价值为：

其中τ∈（0，1），为一给定值，S为种群中个体的总数。

3）父代种群的产生 随机产生区间[0，1]内的S组随机数，每组包含n个，组成初始种群 ｛（yi1，yi2，…，yin）｜i＝1，2，…，S｝。利用（10）式可获得个体 （yi1，yi2，…yin对应的设计参数向量xi＝ （xi1，xi2，…，xin）。利用xi确定的有限元模型的分析结果，可获得对应的目标函数值F（xi）。从小到大对｛F（xi）｝排序，｛（yi1，yi2，…，yin）｝也跟着排序，i＝1，2，…，S，排序后的初始种群称为父代种群。父代种群中最前面的个体称为优秀个体。对父代种群执行如下的遗传运算。

4）遗传运算 （1）选择运算。基于各个体的评价值，采用轮盘赌选择[16]；（2）杂交运算。采用算术杂交[16]；（3）变异运算。采用有向变异[16]。3种遗传运算都产生S个子代个体。

5）演化迭代 对上述的3S个子代个体，按其目标函数值从小到大排序，取其前面的S-k个，加上父代种群的个优秀个体，组成子代种群。算法转入步骤4），进行下一轮演化，执行选择、杂交和变异运算，如此反复。

6）加速方法 优化变量初始化区间的大小决定遗传算法的寻优效率，初始化区间越大，寻优效率越低，且不能保证全局收敛。为了提高寻优效率，算法可采用如下的加速方法：

用父代种群执行3次遗传运算，用第1、3次优秀个体的变化区间作为优化变量新的变化区间，转入3），重新运行遗传算法。通过如上方法，则优秀个体的变化区间逐步缩小，距离最优个体越来越近，直至算法运行达到预定加速次数，算法结束，输出最优个体。

4.6 有限元模型的修正结果

基于目标函数F1（x），F2（x）和前7阶试验模态参数，利用实数编码加速遗传算法，修正初始有限元模型。其中S＝100，交叉和变异概率分别为Pc＝0.8和Pm＝0.01。对算法执行30次运算后收敛。修正后有限元模型分别表示为FEM1和FEM2。对其模态分析且与前7阶试验模态比较，结果如表4所示，其中FEM1和FEM2的计算频率为fU1m和fU2m，与试验频率fEm的相对误差为RU1m和RU2m，振型相关系数为macU1m和macU2m。MAC矩阵如图6所示，频率误差Rm（x）和振型相关系数macm（x）的进化曲线分别如图6、7所示。

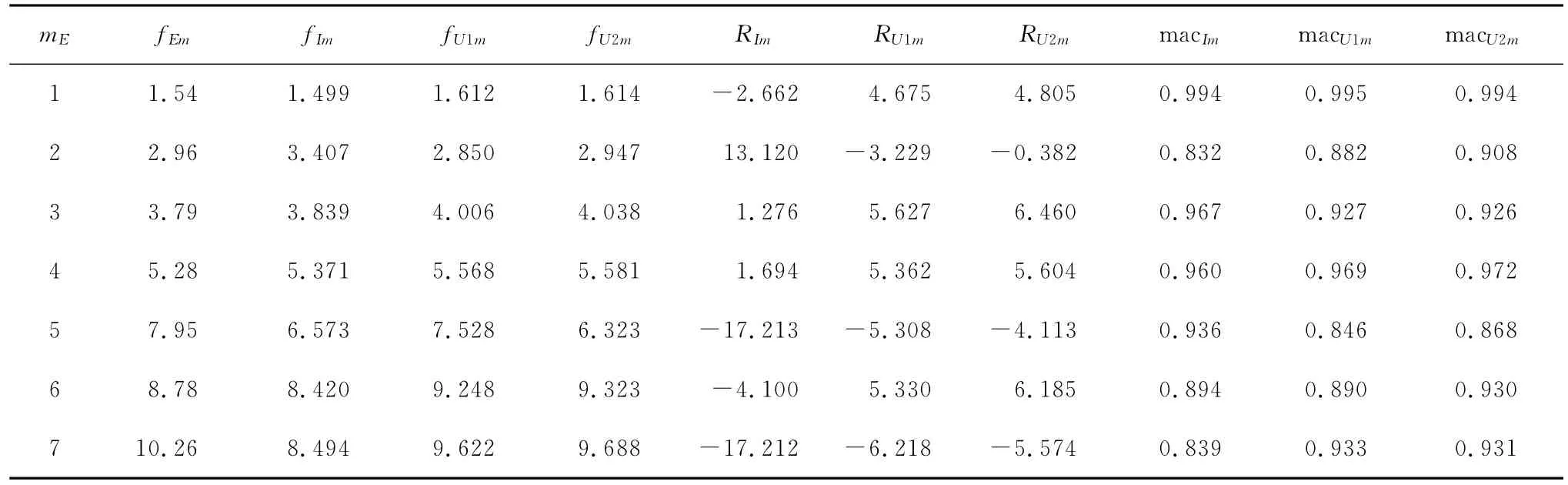
表4 试验模态与分析模态间的比较结果

图6 修正后有限元模型的MAC图

由表4可知，相对于初始有限元模型，基于F1（x），F2（x）修正的 FEM1和 FEM2的前7阶频率相对误差和振型相关系数都有了很大的改善。FEM1的前7阶频率相对误差最大值为6.218%，平均值为5.107%，振型相关系数最小值为0.846，平均值为0.920；FEM2的前7阶频率相对误差最大值为6.460%，平均值为4.732%，振型相关系数最小值为0.868，平均值为0.933。初始有限元模型的频率相对误差的最大值为17.213%，平均值为8.182%，振型相关系数最小值为0.832，平均值为0.917。由此可见，FEM1和FEM2，可以较准确复现实桥修正频段内的试验结果。

图7 和的进化曲线

4.7 有限元模型的预测结果

为了较全面地评估修正后有限元模型的质量，需考察其预测能力，即考察其预测实桥修正频段以外试验结果的能力。现对FEM1和FEM2模态分析，与后3阶试验模态比较，结果如表5所示。

表5 试验模态与预测模态间的比较结果

由表5知，FEM1和FEM2的模态分析结果，与修正频段以外的试验结果相比较，FEM1的频率相对误差最大值为4.331%，平均值为1.536%，振型相关系数最小值为0.863，平均值为0.922；FEM2的频率相对误差最大值为5.748%，平均值为2.976%，振型相关系数最小值为0.872，平均值为0.938。由此可见，FEM1和FEM2，可以较准确预测修正频段外的试验结果。

因此，由修正结果和预测能力知，采用实数编码加速遗传算法，基于目标函数，通过试验模态参数，修正初始有限元模型，可获得较准确反映其动力行为的有限元模型。

6 结 语

1）有限元模型修正的数学模型的概括，及将其转化为多目标优化问题，奠定了实数编码加速遗传算法应用于有限元模型修正问题的基础。

2）建立合适的目标函数，采用适当的编码方法，是发挥遗传算法优势的基础。本文基于频率指标与振型相关系数指标定义目标函数，从而保证了模型修正的良好结果。同时，实数编码的采用，提高了模型修正的精度。加速方法的应用，节省了模型修正的时间和提高了效率。

3）从修正效果看，修正频段内的频率相对误差都在内，振型相关系数都大于8.0，平均值大于9.0；修正频段外的频率相对误差都在内，平均值小于，振型相关系数都大于8.5，平均值大于9.0。因此，本文采用的实数编码加速遗传算法对提高模型修正的精度和计算效率都有很好的作用，可获得较准确反映桥梁实际动力行为的有限元模型。

[1]林贤坤，张令弥，郭勤涛，等.基于模态挠度法的预应力连续箱梁桥状态评估[J].土木工程学报，2010，43（10）：83-90.LIN Xiankun，ZHANG Lingmi，GUO Qintao，et al.Application of modal deflection method for condition assessment of prestressed concrete continuous boxgirder bridges [J].China Civil Engineering Journal，2010，43（10）：83-90.

[2]Zhang Q W，Chang C C，Chang T Y P.Finite element model updating for structures with parametric constraints[J].Earthquake Engineering and Structural Dynamics，2000，29：927-944.

[3]Teuguels A，Maeck J，Roeck G D.Damage assessment by FE model updating using damage functions[J].Composite Structures，2002，80：1869-1879.

[4]Ambrogio W D，Fregolent A.Results obtained by minimising natural frequency and antiresonance errors of a beam model[J].Mechanical Systems and Signal Processing，2003，17（1）：29-37.

[5]Hanson D，Waters T P，Thompson D J，et al.The role of anti-resonance frequencies from operational modal analysis in finite element model updating[J].Mechanical Systems and Signal Processing，2007，21（1）：74-97.

[6]Teughels A，Maeck J，Roeck G D.A finite element model updating method using experimental modal parameters applied on a railway bridge [C]／／Proceedings of 7th International Conference on Computer Aided Optimum Design of Structures，Bologna，Italy，May，2001：97-106.

[7]Mottershead J E，Friswell M I.Model updating in structural dynamics：a survey[J].Journal of Sound and Vibration，1993，167：347-375.

[8]夏品奇，Brownjohn J M W.斜拉桥有限元建模与模型修正[J].振动工程学报，2003，16（2）：219-223.XIA Pinqi，Brownjohn J M W.Finite element modeling and model updating of a cable-stayed bridge[J].Journal of Vibration Engineering，2003，16（2）：119-223.

[9]费庆国，张令弥，李爱群，等.基于统计分析技术的有限元模型修正研究[J].振动与冲击，2005，24（3）：23-26.FEI Qingguo，ZHANG Lingmi，LI Aiqun，et al.Finite element model updating using statistics analysis[J].Journal of Vibration and Shock，2005，24（3）：23-26.

[10]余岭，万祖勇，朱宏平，等.基于POS算法的结构模型修正与损伤检测[J].振动与冲击，2006，25（5）：37-39.YU Ling，WAN Zuyong，ZHU Hongping，et al.Structural model updating and damage detection through particle swarm optimization [J].Journal of Vibration and Shock，2006，25（5）：37-39.

[11]周星德，明宝华，潘瑞鸿，等.基于遗传算法的降阶模型修正方法研究[J].振动、测试与诊断，2007，27（1）：25-28.ZHOU Xingde，MING Baohua，PAN Ruihong，et al.Research on modification of model reduction based on genetic algorithms journal of vibration[J].Journal of Vibration，Measurement ＆ Diagnosis，2007，27（1）：25-28.

[12]费庆国，李爱群，张令弥.基于神经网络的非线性结构有限元模型修正研究[J].宇航学报，2005，26（3）：267-269.FEI Qingguo，LI Aiqun，ZHANG Lingmi.Study on finite element model updating of nonlinear structures using neural network [J].Journal of Astronautics，2005，26（3）：267-269.

[13]Zhang L M，Wang T，Yukio T.A frequency-spatial domain decomposition（FSDD）method for operational modal analysis [J].Mechanical Systems and Signal Processing，2010，24：1227-1239.

[14]王彤，张令弥.运行模态分析的频域空间域分解法及其应用[J].航空学报，2006，27（1）：62-66.WANG Tong，ZHANG Lingmi.Frequency and spatial domain decomposition for operational modal analysis and its application [J].Acta Aeronautica Et Astronautica Sinica，2006，27（1）：62-66.

[15]玄光男，程润伟.遗传算法与工程优化[M].于歆杰，周根贵，译.清华大学出版社，2004，1-7，22，25.