GPS动态定位自适应卡尔曼滤波算法研究

李勇军，左 娟

（1.江西省测绘应急保障服务中心，江西 南昌 330046；2.江西省第一测绘院，江西南昌 330046）

GPS动态定位自适应卡尔曼滤波算法研究

李勇军1，左 娟2

（1.江西省测绘应急保障服务中心，江西 南昌 330046；2.江西省第一测绘院，江西南昌 330046）

Sage－Husa滤波和强跟踪滤波是2种常规的自适应卡尔曼滤波，有各自的优缺点。综合2种滤波的特点，给出一种抗粗差的修正算法，实验效果比较好，能有效抑制少部分粗差带来的影响，计算结果表明效果比较理想。

动态GPS定位；卡尔曼滤波；自适应滤波；Sage－Husa滤波；强跟踪滤波

卡尔曼滤波是一个不断预测、修正的递推过程，求解时不需要存储大量的观测数据，并且当得到新的观测数据时，可随时算得新的参数滤波值，便于实时地处理观测结果，因此，越来越多地应用于动态定位数据处理中，尤其是GPS动态数据处理［1－3］。然而，在一般情况下，Kalman滤波所基于的动力学模型和随机模型不可能准确无误。特别是带有粗差的样本数据常常会使卡尔曼滤波器对系统的状态预报进行错误的修正，使得滤波结果发生偏移，甚至发散。因此，在卡尔曼滤波中加入抗粗差处理是非常必要的。

1 常见的自适应卡尔曼滤波模型

在GPS动态单点定位中，一般采用常加速模型（CA模型［4］），卡尔曼滤波系统的状态方程和观测方程可表示为

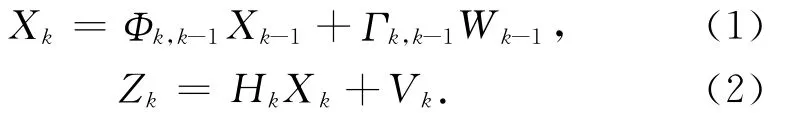
式中：X为状态矢量，X＝（xyzt˙x˙y˙z ˙t¨x¨y¨z¨t）T，Φk，k－1是状态转移矩阵，Γk，k－1是噪声输入矩阵，Wk是过程噪声矢量，Zk是观测矢量，Hk是伪距观测线性化后的观测矩阵，Vk是观测方程的误差矢量。

1.1Sage－Husa自适应滤波

Sage自适应滤波［5－7］利用历史信息的平均来估计当前历元的动态噪声协方差矩阵和观测噪声协方差矩阵，从而使动态噪声协方差矩阵和观测噪声协方差矩阵自适应于当前的动态信息和观测信息。线性系统的Sage－Husa自适应滤波可以描述为

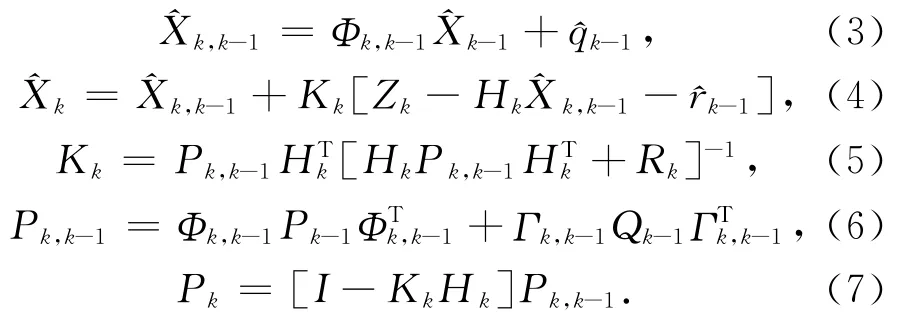
式中：Qk是系统过程噪声，Rk是系统观测噪声，Kk为增益矩阵，Pk为预测值方差阵，＾qk、＾Qk、＾rk、＾Rk由时变噪声统计估计器［8］递推获得，其中：

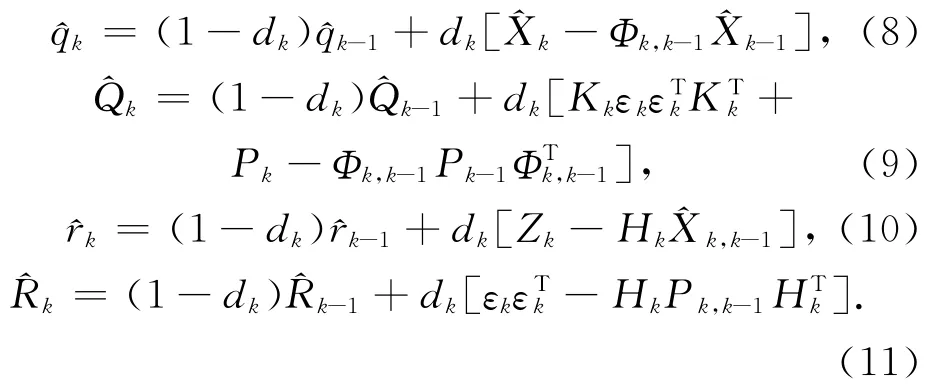
在应用Sage自适应滤波处理动态GPS观测数据时，由于动态定位中的状态变量维数比较高，Sage－Husa算法对于阶次较高的系统也不能保证完全可靠，有可能失去半正定性和正定性而出现滤波发散现象，稳定性和收敛性不能完全保证［2］。

1.2 强跟踪kalman滤波

强跟踪算法［9－11］，即采用渐消因子限制Kalman滤波器的记忆长度，以便充分利用现时的观测数据。与正常Kalman滤波解的显著区别在于将验前状态协方差矩阵膨胀λk倍，使历史状态信息的试用效率降低，从而达到重用现时测量信息的目的，如式（12）所示。

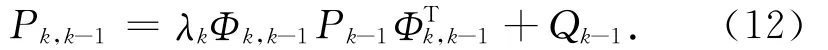
式中：λk＝diag［λ1kλ2k… λnk］，λk为渐消因子，有时候也称为遗忘因子，且λk≥1。

最佳遗忘因子λk可由下式求取：

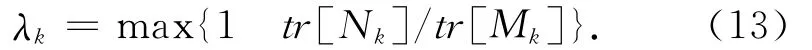
式中：tr［·］是矩阵求迹符号，Nk和Mk的表达式为

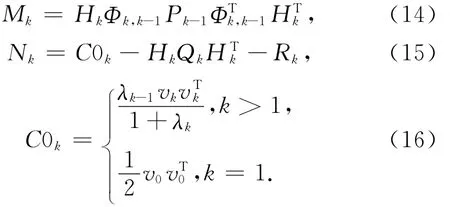
式中：vk＝Zk－Hk

2 一种改进的自适应滤波

带有粗差的样本数据常常会使Kalman滤波器对系统的状态预报进行错误的修正，使得滤波结果发生偏移，甚至发散。因此，在Kalman滤波中，加入必要的抗粗差处理是非常必要的。

2.1 抗粗差修正算法

当测量数据中含少量粗差时，能够克服其不利影响，或者能将其影响控制在某预先给定的界限内，以确保滤波估计值尽可能接近系统真实状态。由此构造了自适应Kalman滤波的抗粗差修正算法如下：

式中：Yk（·）为适当选取的按段光滑的函数，称为压缩影响函数；Gk为权矩阵。如果选取权矩阵序列

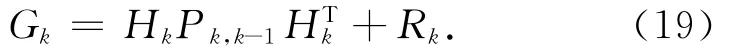
则使滤波误差均方差最小的Y函数为

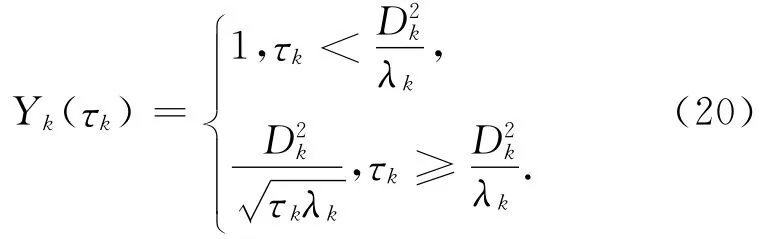
式中：λk为KkGk矩阵的最大特征值，Dk为选取的门限常数序列，Dk的合理取值为

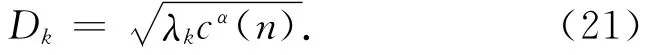
式中：cα（n）为以χ2（n）分布置信度为（1－α）×100%的上分位点，通常α取0.05或0.025。

2.2 滤波器收敛性判据

当滤波器发散时，误差协方差阵无界，这时实际的误差往往比理论预计的误差大很多倍。可以根据这一特点，利用新息序列的性质来构造滤波器的收敛判据。

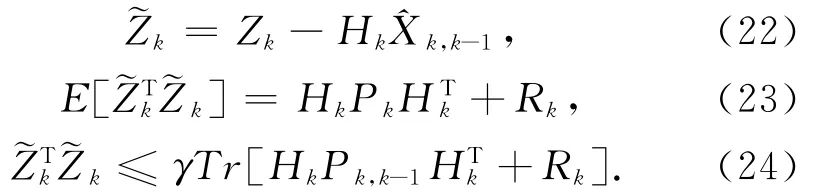
式中：γ≥1为可调系数。

2.3 算法流程

当式（24）成立时，测量值Zk为正常测量值，滤波器处于正常工作状态，这时可用Sage－Husa自适应滤波算法进行状态最优值估计。反之，说明测量值Zk为粗差或滤波发散，此时如果仅采用强跟踪滤波算法，滤波的最优条件将被破坏，导致滤波精度降低；如果仅采用抗粗差修正算法处理，又无法保证滤波的稳定性和准确性。实际上，GPS观测时，成片粗差的个数是有限的。因此，本文设置了一个连续粗差个数门限，当连续粗差的个数小于门限值时，将当前测量值视为粗差，采用抗粗差修正算法处理，即进行状态估计时利用压缩影响函数Yk（）抑制由粗差带来的异常信息，使状态估计保持正常；否则，认为滤波发散，采用强跟踪滤波算法处理，即利用加权系数λk调整Pk，k－1，从而抑制滤波发散。

3 实例分析

本文算例数据选自丹麦国家空间研究中心（DNSC）在格陵兰地区进行航空Lidar测量所采集的动态GPS数据［12］，采用武汉大学测绘学院开发的动态定位软件TriP2.0计算的结果作为“已知值”（动态定位精度：3cm～1dm）。实验选用了前2000个历元作为实验的数据，在这2000个历元当中，飞机完成了从“静止→起飞→升空→平稳”的一系列机动突变的过程，具有代表性，能比较好地分析其动态定位。

实验采用如下5种方案（见图1～图5）进行计算比较：方案A：单历元最小二乘平差解；方案B：标准Kalman滤波解；方案C：Sage－Husa自适应滤波解；方案D：强跟踪自适应滤波解；方案E：改进自适应滤波解。为节省空间，在此仅选择各种方案在X轴方向与参考值的差值图。

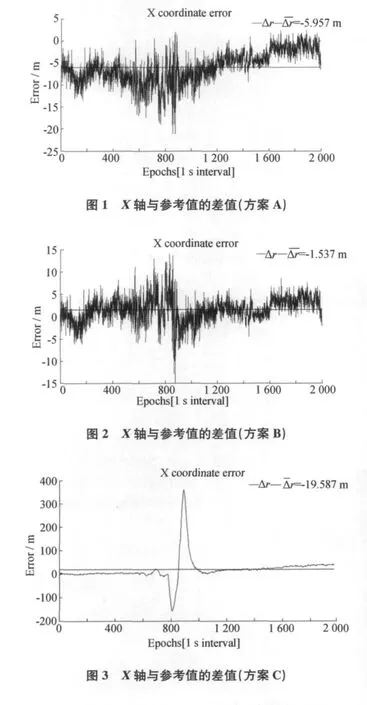
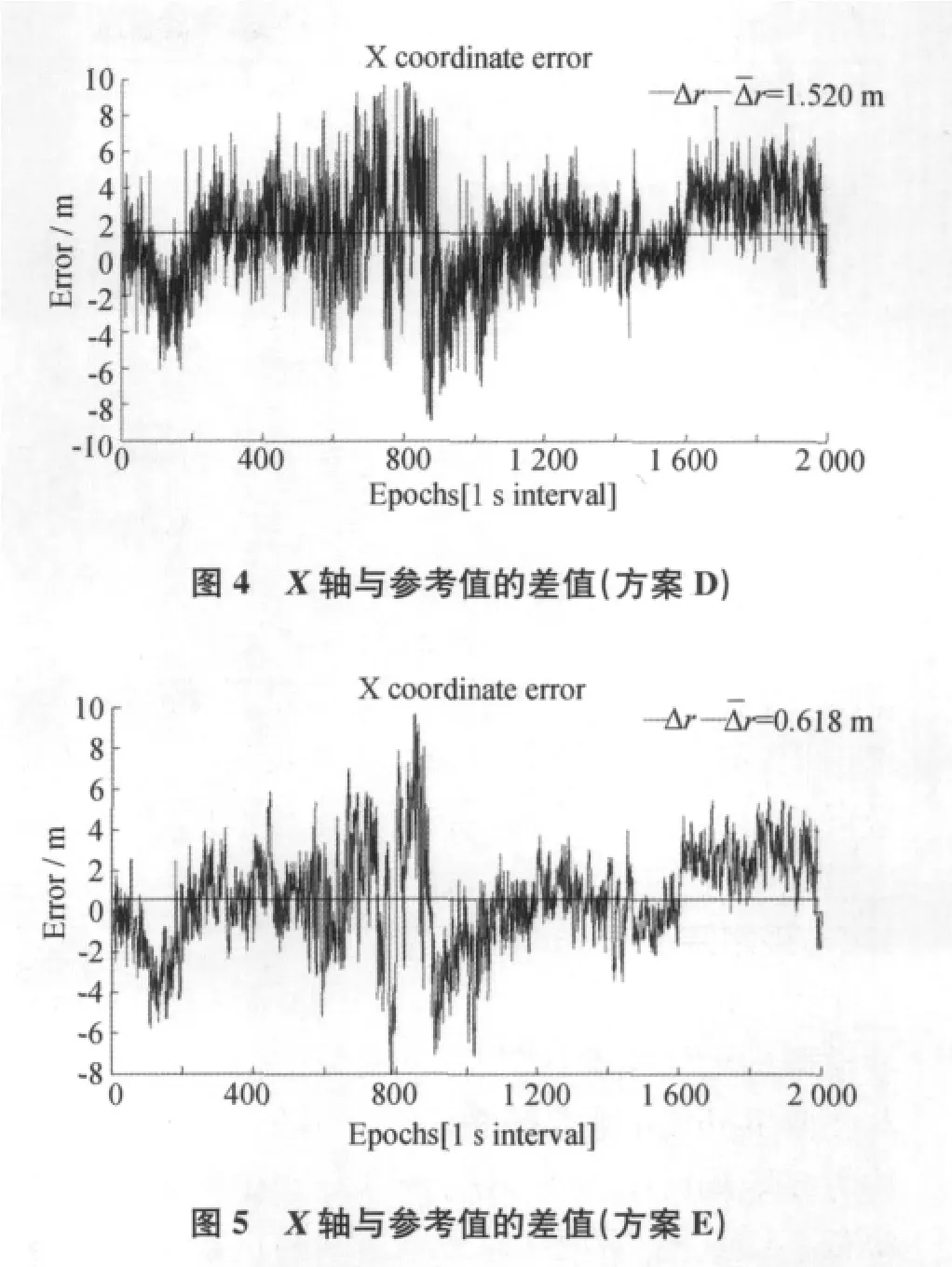
从上面5个方案计算的结果（见表1），可以看出：

1）飞机起飞的时候，标准的kalman滤波和Sage－Husa自适应滤波的结果受到明显影响，尤其是Sage－Husa自适应滤波，出现了发散。最小二乘估计基本上不受飞机扰动的影响，强跟踪自适应滤波受飞机扰动影响不大，而改进的自适应滤波对飞机的扰动能够自适应，效果明显，具有抵抗非平稳的能力。

2）当观测值存在粗差时，Sage－Husa自适应滤波比标准的kalman滤波还要差，甚至发散（本例即为发散）。观测值粗差歪曲了当前历元的结果，而将预测信息与观测信息的不符合全部归咎于预报信息，于是过分降低了预报信息的权重，使自适应滤波的结果拟合于错误的观测结果。

3）强跟踪算法虽然在对突变情况进行估计的时候，精度不是很好，但是比较稳定，增大了系统的过程噪声和观测噪声的方差阵，保证了滤波可靠收敛，但是牺牲一定精度而换取滤波的稳定性。

4）改进的自适应滤波不仅能抵制机动目标的突变情况，而且还能抵御小部分粗差的影响，能合理平衡动力学模型预报信息与观测信息的权比，对状态扰动的影响具有较强的控制能力。

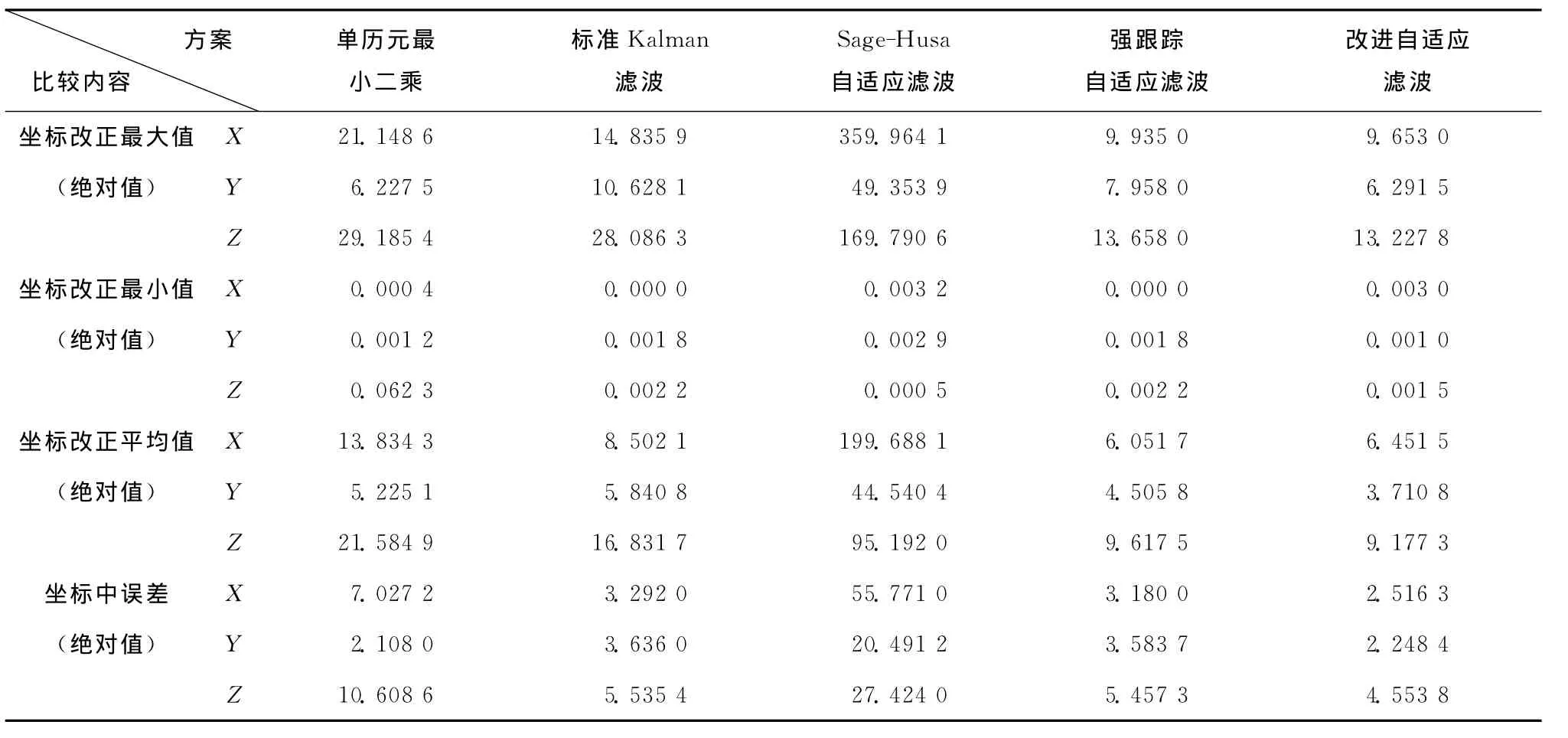
表1 5种不同方案计算的X、Y、 Z方向坐标与参考值之差统计情况m

4 结 论

综合以上分析，可以得出：

1）标准kalman滤波能够充分利用预报信息来提高滤波估值的精度，但不能控制载体运动扰动异常误差的影响；

2）最小二乘估计可以有效抵制载体运行异常误差的影响，但没有充分利用载体平稳运行的可靠预报信息；

3）Sage－Husa自适应滤波能够合理利用预报信息和当前历元信息来对滤波进行估值，但前提是要前一历元能为当前历元提供可靠估值，否则容易发散；

4）强跟踪算法虽然能够防止滤波发散，但是增大系统的过程噪声和观测噪声方差阵，这样将许多未建模的误差包含进去，使滤波稳定，但降低了部分精度；

5）改进的自适应滤波不仅能够有效抵制观测值粗差的影响，而且能够合理平衡模型预报信息和当前历元观测信息。

［1］秦永元，张洪鉞，汪叔华.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，1998.

［2］付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用［M］.北京：科学出版社，2003.

［3］刘基余.GPS卫星导航定位原理与方法［M］.北京：科学出版社，2003.

［4］杨元喜.自适应动态导航定位［M］.北京：科学出版社，2006.

［5］Sage A P，Husa G W.Adaptive Filtering With unknown Prior Statistic.Joint Automatic Control Conference，1969：760－769.

［6］Mohamed A H，Schwarz K P.Adaptive Kalman filter for INS／GPS［J］.Journal of Geodesy，1999，73（4）：193－203.

［7］Wang Y J，Stewart M P，Tsakiri M.Adaptive Kalman filtering for integration of GPS with GLONASS and INS［C］.IUGG／IAG Birmingham，August：18－31.

［8］王永刚，王顺宏.改进Sage－Husa滤波及在GPS／INS容错组合制导中的应用［J］.中国惯性技术学报，2003，11（5）：29－32.

［9］Fagin S L.Recursive Linear regession theory，optimal filter theory and error analysis of optimal system［J］.IEEE Int.Convent，Record，.1964，12：216－240.

［10］夏启军，孙优贤，周春晖.渐卡尔曼滤波器的最佳自适应算法及其应用［J］.自动化学报，1990，16（3）：210－216.

［11］蔡艳辉，程鹏飞，李夕银.用卡尔曼滤波进行GPS动态定位［J］.测绘通报，2006（7）：6－8.

［12］张小红.动态精密单点定位（PPP）的精度分析［J］.全球定位系统，2006（1）：7－11.

Research on adaptive Kalman Filtering algorithm in GPS kinematic positioning

LI Yong－jun1，ZUO Juan2
（1.Jiangxi Emergency Guarantee Service Center of Surveying and Mapping，Nanchang 330046，China；2.Jiangxi First Surveying and Mapping Institute，Nanchang 330046，China）

Sage－Husa adaptive filtering and strong tracking adaptive filtering are two general adaptive Kalman filters，but they both have advantages and disadvantages.The paper proposes an approach to antigross error correction algorithm by combination of the filers above based on the filter divergence analysis.Experimental results were quite good and can inhibit the small impact of gross errors.

dynamic GPS positioning；Kalman filtering；adaptive filtering；Sage－Husa adaptive filtering；strong tracking adaptive filtering

P228

A

1006－7949（2012）04－0029－04

2011－07－12

李勇军（1984－），男，助理工程师，硕士.

[责任编辑:刘文霞］