刍议分段函数在分段点处的导数

靳 强，郭玉琼(十堰市柳林中学，湖北 十堰 442000)

刍议分段函数在分段点处的导数

靳 强，郭玉琼(十堰市柳林中学，湖北 十堰 442000)

在讨论分段函数在分段点处的导数时，初学者往往容易对分段点2边的函数表达式利用导数的基本公式和运算法则求导，然后分别取极限来判定。分析了利用导数的基本公式讨论分段函数在分段点处的导数中存在的问题，并给出了该方法可行性的特定条件。

分段函数；分段点；导数；连续

对于求分段函数在分段点处的导数及判定导数存在与否，常用的方法有如下2种：该点不连续则该点必不可导；利用导数的定义来判定左右导数是否存在相等。

对于微积分的初学者来说，求函数导数最简便方法是利用导数的基本公式和运算法则，故出现很多初学者对于求分段点处的导数不采用导数定义来讨论的情况，而是直接利用导数的基本公式和运算法则求导，然后再取极限或直接代入。由于分段函数本身具有的特性不一样，有时候该种方法求分段点处导数是可行的，有时候则不然，这让很多初学者产生了很大的困惑。为此，笔者通过实例对该类问题进行了分析说明，并给出了该方法的可行性特定条件。

1 实例分析

解法1因为：

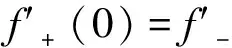
解法2因为：

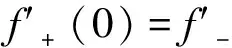
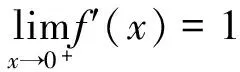
巧合的是这2种解法的结果又是完全正确的，这是偶然还是必然？如果是必然，那理论依据是什么？

2 用导数的基本公式讨论分段函数在分段点处的导数可行性的条件

该导数的极限定理同样也适合求分段函数的导数。

定理2的证明和定理1基本类似，这里就不加详述。有了定理2的理论支撑，那么例1中解法2的正确性就不是偶然的。但也要注意对于定理2的使用的条件，不然也会出现纰漏。

对例1稍加修改得到下述例题：

解因为：

但利用导数的定义求解：

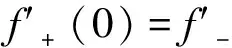
一个题2种解法得出2个不同的答案，似乎都对，真正的问题出在哪里？

3 结 语

综合上面的讨论，实际上对于分段函数在分段点处导数是否存在的问题，用导数的定义来求解是最广泛适用的方法。上述的2个定理也为初学者提供了一种新思路，更重要的是找到了容易产生混淆和困惑的地方。

[1]华东师范大学数学系.数学分析(上)[M].北京：高等教育出版社, 2003.

[2] 彭娟,郭夕敬.分段函数在分段点处的导数[J].高等数学研究, 2009, 12(5):19-21.

[编辑] 洪云飞

O172.1

A

1673-1409(2012)05-N011-02

10.3969/j.issn.1673-1409(N).2012.05.005

2012-02-25

靳强(1977-)，男，2001年大学毕业，中学高级教师，现主要从事数学理论方面的教学与研究工作。